山东省安丘市青云学府2023届高三下学期数学一模试卷
试卷更新日期:2023-04-03 类型:高考模拟
一、单选题
-
1. 若复数满足 , 则( )A、4 B、 C、16 D、172. 已知集合 , 则( )A、 B、 C、 D、3. 下列说法正确的是( )A、“”是“”的充要条件 B、“”是“”的必要不充分条件 C、命题“”的否定形式是“” D、“”是“”的充分不必要条件4. 紫砂壶是中国特有的手工制造陶土工艺品,其制作始于明朝正德年间.紫砂壶的壶型众多,经典的有西施壶、掇球壶、石瓢壶、潘壶等.其中石瓢壶的壶体可以近似看成一个圆台,如图给出了一个石瓢壶的相关数据(单位:cm),现在向这个空石瓢壶中加入(约)的矿泉水后,问石瓢壶内水深约( )cm
 A、2.8 B、2.9 C、3.0 D、3.15. 已知函数则函数的图象大致是( )A、
A、2.8 B、2.9 C、3.0 D、3.15. 已知函数则函数的图象大致是( )A、 B、
B、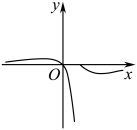 C、
C、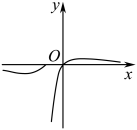 D、
D、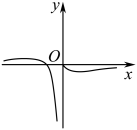 6. 已知平面向量满足 , 且 , 则的最大值为( )A、 B、 C、 D、7. 若正实数a,b满足 , 且 , 则下列不等式一定成立的是( )A、 B、 C、 D、8. 已知是数列的前项和,且 , (),则下列结论正确的是( )A、数列为等比数列 B、数列为等比数列 C、 D、
6. 已知平面向量满足 , 且 , 则的最大值为( )A、 B、 C、 D、7. 若正实数a,b满足 , 且 , 则下列不等式一定成立的是( )A、 B、 C、 D、8. 已知是数列的前项和,且 , (),则下列结论正确的是( )A、数列为等比数列 B、数列为等比数列 C、 D、二、多选题
-
9. 下列命题中,真命题的是( )A、若样本数据的方差为2,则数据的方差为8 B、若回归方程为 , 则变量y与x负相关 C、甲同学所在的某校高三共有5003人,先剔除3人,再按简单随机抽样的方法抽取容量为200的一个样本,则甲被抽到的概率为 D、在线性回归分析中相关指数用来刻画回归的效果,若值越小,则模型的拟合效果越好10. 将函数的图象向右平移个单位长度得到的图象,则( )A、在上是减函数 B、 C、是奇函数 D、在上有4个零点11. 已知是圆上的两点,则下列结论中正确的是( )A、若 , 则 B、若点O到直线的距离为 , 则 C、若 , 则的最大值为4 D、的最小值为-412. 如图,已知直四棱柱ABCD-EFGH的底面是边长为4的正方形, , 点M为CG的中点,点P为底面EFGH上的动点,则( )
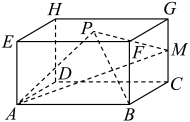 A、当时,存在点P满足 B、当时,存在唯一的点P满足 C、当时,满足BP⊥AM的点P的轨迹长度为 D、当时,满足的点P轨迹长度为
A、当时,存在点P满足 B、当时,存在唯一的点P满足 C、当时,满足BP⊥AM的点P的轨迹长度为 D、当时,满足的点P轨迹长度为三、填空题
-
13. 在展开式中,含的项的系数是.(用数字作答)14. 已知红箱内有5个红球、3个白球,白箱内有3个红球、5个白球.第一次从红箱内取出一球,观察颜色后放回原处;第二次从与第一次取出的球颜色相同的箱子内再取出一球,则第二次取到红球的概率为.15. 已知双曲线右焦点为 , 点P,Q在双曲线上,且关于原点O对称.若 , 且的面积为4,则双曲线的离心率 .16. 已知关于的不等式恒成立,则实数的取值范围为.
四、解答题
-
17. 已知等比数列的前项和为 , , .(1)、求数列的通项公式.(2)、令 , 求数列的前项和.18. 在中,设角A,B,C所对的边分别为a,b,c,且满足 .(1)、求证:;(2)、求的最小值.19. 在三棱锥中, , 平面 , 点是棱上的动点,点是棱上的动点,且.
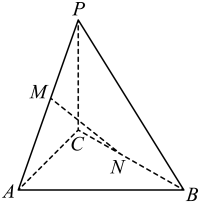 (1)、当时,求证:;(2)、当的长最小时,求二面角的余弦值20. 常益长高铁的试运营,标志着我省迈入“市市通高铁”的新时代.常益长高铁全线长157公里,共设有常德站、汉寿站、益阳南站、宁乡西站、长沙西站5个车站. 在试运营期间,铁路公司随机选取了乘坐常德开往长沙西站G6575次复兴号列车的名乘客,记录了他们的乘车情况,得到下表(单位:人):
(1)、当时,求证:;(2)、当的长最小时,求二面角的余弦值20. 常益长高铁的试运营,标志着我省迈入“市市通高铁”的新时代.常益长高铁全线长157公里,共设有常德站、汉寿站、益阳南站、宁乡西站、长沙西站5个车站. 在试运营期间,铁路公司随机选取了乘坐常德开往长沙西站G6575次复兴号列车的名乘客,记录了他们的乘车情况,得到下表(单位:人):下车站上车站
汉寿站
益阳南站
宁乡西站
长沙西站
总计
常德站
10
20
10
40
80
汉寿站
10
10
20
40
益阳南站
10
40
50
宁乡西站
30
30
总计
10
30
30
130
200
(用频率代替概率)
(1)、从这200名乘客中任选一人,求该乘客仅乘坐一站的概率;(2)、在试营运期间,从常德上车的乘客中任选3人,设这3人到长沙西站下车的人数为X,求X的分布列,及其期望;(3)、已知德山经开区的居民到常德站乘车的概率为0.6,到汉寿站乘车的概率为0.4,若经过益阳南站后高铁上有一位来自德山经开区的乘客,求该乘客到长沙西站下车的概率.