吉林省长春市绿园区2021-2022学年九年级(下)期初数学试卷
试卷更新日期:2023-04-03 类型:开学考试
一、选择题(本大题共8小题,每小题3分,共24分)
-
1. ﹣4的绝对值是( )A、4 B、﹣4 C、 D、2. 电影《长津湖之水门桥》上映后,票房一路高歌,2022年2月9日单7票房为113000000元,113000000用科学记数法可表示为()A、11.3×108 B、1.13×108 C、1.13×109 D、1.13×1073. 如图是一个几何体的三视图,则这个几间体是( )
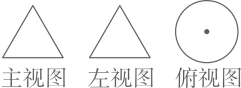 A、圆锥 B、圆柱 C、三棱柱 D、三棱锥4. 在数轴上表示不等式3x+1≤-5的解集,正确的是( )A、
A、圆锥 B、圆柱 C、三棱柱 D、三棱锥4. 在数轴上表示不等式3x+1≤-5的解集,正确的是( )A、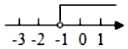 B、
B、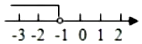 C、
C、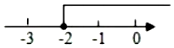 D、
D、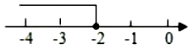 5. 关于x的一元二次方程x2-2x+2=3k有两个不相等的实数根,则k的取值范围为( )A、k> B、k>1 C、k<1 D、k>6. 如图,在大风来临之前,有关部门用钢管加固树木,固定点A离地面的高度AC=m,钢管与地面所成角∠ABC=∠1,那么钢管AB的长为()
5. 关于x的一元二次方程x2-2x+2=3k有两个不相等的实数根,则k的取值范围为( )A、k> B、k>1 C、k<1 D、k>6. 如图,在大风来临之前,有关部门用钢管加固树木,固定点A离地面的高度AC=m,钢管与地面所成角∠ABC=∠1,那么钢管AB的长为()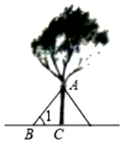 A、 B、 C、m•cos∠1 D、m•sin∠17. 在△ABC中,∠BAC=90°,AB>AC,∠C≠60°,用无刻度的直尺和圆规在BC边上找一点D,使AD=BD,下列作法正确的是()A、
A、 B、 C、m•cos∠1 D、m•sin∠17. 在△ABC中,∠BAC=90°,AB>AC,∠C≠60°,用无刻度的直尺和圆规在BC边上找一点D,使AD=BD,下列作法正确的是()A、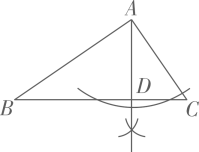 B、
B、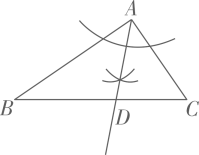 C、
C、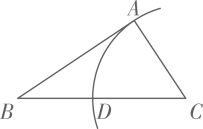 D、
D、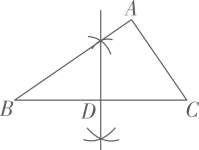 8. 如图,在平面直角坐标系中,点P是反比例函数y=(x>0)图象上一点,点B的坐标为(1,0),点A是y轴正半轴上一点,且AP⊥BP,AP:BP=1:2,那么四边形AOBP的面积为()
8. 如图,在平面直角坐标系中,点P是反比例函数y=(x>0)图象上一点,点B的坐标为(1,0),点A是y轴正半轴上一点,且AP⊥BP,AP:BP=1:2,那么四边形AOBP的面积为() A、6.5 B、8 C、10 D、7
A、6.5 B、8 C、10 D、7二、填空题(本大题共6小题,每小题3分,共18分)
-
9. 小明x岁,小华比小明岁数的2倍大5岁,则小华岁.10. 分解因式:x3﹣xy2= .11. 如图,已知直线AB,CD被EF所截,EG是∠AEF的角平分线,若∠1=∠2,∠2+∠4=120°,则∠3=°.
 12. 已知一个多边形的内角和为1440°,那么它是 边形.13. 如图在平面直角坐标系中,矩形OABC的顶点坐标分别是O(0,0),C(6,0),B(6,4),A(0,4),已知矩形OA'B'C与矩形OABC位似,位似中心是原点O,矩形OA'BC'的面积等于矩形OABC面积的 , 且点B不在第一象限,则点B'的坐标是
12. 已知一个多边形的内角和为1440°,那么它是 边形.13. 如图在平面直角坐标系中,矩形OABC的顶点坐标分别是O(0,0),C(6,0),B(6,4),A(0,4),已知矩形OA'B'C与矩形OABC位似,位似中心是原点O,矩形OA'BC'的面积等于矩形OABC面积的 , 且点B不在第一象限,则点B'的坐标是
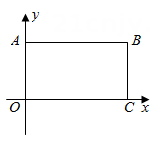 14. 在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的部分图象如图所示,其对称轴为直线x=1,与y轴交于(0,-3),则当y<-3时,x的取值范围是
14. 在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的部分图象如图所示,其对称轴为直线x=1,与y轴交于(0,-3),则当y<-3时,x的取值范围是
三、解答题(本大题共10小题,共78分)
-
15. 先化简,再求值:(x+5)(x-1)+(x-2)2 , 其中x= .16. 在一个不透明的口袋中装有4个乒乓球,球面上分别标有数字-1,2,-3,4.每个乒乓球除数字不同外其余均相同.(1)、摇匀后任意摸出1个球,则摸出的乒乓球面上的数是负数的概率为(2)、摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球的球面上的数学上和是正数的概率,17. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连结DE,F为线段DE上一点,且∠AFE=∠B.
 (1)、求证:△ADF∽△DEC:(2)、若AE=6,AD=8,AB=7,则AF的长为18. 我国5G网络和终端商的快速发展,使得新一轮5G建设蓄势待发.某大型5G设备生产商为加快生产速度,现在平均每天比原计划多生产50万件设备,现在生产600万件设备与原来生产500万件设备所需时间相同,问:原计划每天生产多少万件设备?19. 图①、图②、图③均是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,只用无刻度的直尺,在图①、图②、图③中各画一个三角形,要求同时满足以下三个条件:
(1)、求证:△ADF∽△DEC:(2)、若AE=6,AD=8,AB=7,则AF的长为18. 我国5G网络和终端商的快速发展,使得新一轮5G建设蓄势待发.某大型5G设备生产商为加快生产速度,现在平均每天比原计划多生产50万件设备,现在生产600万件设备与原来生产500万件设备所需时间相同,问:原计划每天生产多少万件设备?19. 图①、图②、图③均是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,只用无刻度的直尺,在图①、图②、图③中各画一个三角形,要求同时满足以下三个条件: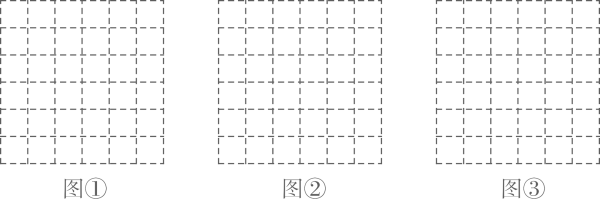 (1)、三角形的顶点在格点上;(2)、三角形是腰长为无理数的等腰三角形;(3)、三角形的面积为6.20. 2021年4月12日,吉林省统计局发布了《吉林省2020年国民经济和社会发展统计公报》,如图是公报中发布的全省“2016一2020年民用汽车保有量及其增长速度”统计图.
(1)、三角形的顶点在格点上;(2)、三角形是腰长为无理数的等腰三角形;(3)、三角形的面积为6.20. 2021年4月12日,吉林省统计局发布了《吉林省2020年国民经济和社会发展统计公报》,如图是公报中发布的全省“2016一2020年民用汽车保有量及其增长速度”统计图.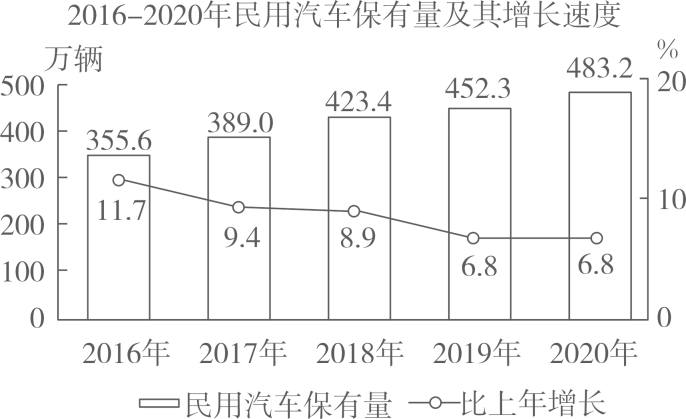 (1)、2020年,全省民用汽车保有量是万辆,比2019年增长了 %.(2)、2016-2020年,全省民用汽车保有量增长速度的众数是 %.(3)、小李看了统计图后说:“图中表示2016-2019年增长速度的折线呈下降趋势,说明2016-2019年全省民用汽车保有量逐年减少.”小李的说法正确吗?请说明理由.(4)、若2022年全省民用汽车保有量能达到584.672万辆,则全省2021年、2022年民用汽车保有量的年平均增长速度为 %.21. 将一些相同规格的长方形纸按图①所示方法粘合起来,粘合部分的宽相等.某学校数学综合与实践小组从函数角度进行了如下探究:
(1)、2020年,全省民用汽车保有量是万辆,比2019年增长了 %.(2)、2016-2020年,全省民用汽车保有量增长速度的众数是 %.(3)、小李看了统计图后说:“图中表示2016-2019年增长速度的折线呈下降趋势,说明2016-2019年全省民用汽车保有量逐年减少.”小李的说法正确吗?请说明理由.(4)、若2022年全省民用汽车保有量能达到584.672万辆,则全省2021年、2022年民用汽车保有量的年平均增长速度为 %.21. 将一些相同规格的长方形纸按图①所示方法粘合起来,粘合部分的宽相等.某学校数学综合与实践小组从函数角度进行了如下探究: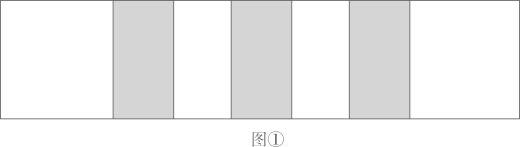
[观察测量]数学综合与实践小组通过观察测量,得到如表:
长方形纸x(张)
1
2
3
4
5
总长度y(厘米)
15
25
35
45
55
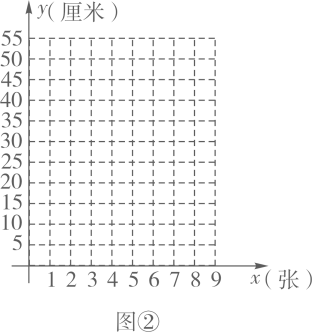 (1)、[探究发现]①建立平面直角坐标系,如图②,横轴表示长方形纸张数石纵轴表示粘合后的总长度y,描出以表格中数据为坐标的各点
(1)、[探究发现]①建立平面直角坐标系,如图②,横轴表示长方形纸张数石纵轴表示粘合后的总长度y,描出以表格中数据为坐标的各点②观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如过不在同一条直线上,说明理由.
(2)、[结论应用]应用上述发现的规律让算①当x=20时,粘合后的纸条总长度y为厘米.
②粘合后内纸条总长度y为505厘米时,需使用长方形纸张.
22. [实践与探究]将△ABC(AB>AC)沿AD折叠,使点C刚好落在AB边上的点E处,展开如图,
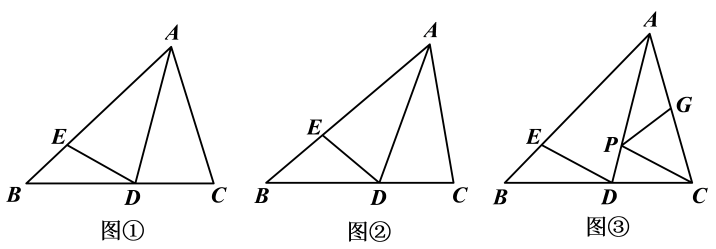 (1)、[操作观察]图①中,AB=8,AC=6.
(1)、[操作观察]图①中,AB=8,AC=6.①BE= .
②若△ACD的面积是9,则△ABD的面积是 .
(2)、[理解应用]如图②,若∠C=2∠B,试说明:AB=AC+CD.(3)、[拓展延伸]如图③,若∠BAC=60°,点G为AC的中点,且AG=5.点P是AD上的一个动点,连结PG、PC,直接写出(PG+PC)2的最小值.23. 如图,在矩形ABCD中,BC=8,tan∠BAC= , 点PM点P从点B出发,沿BC以每秒2个单位长度的速度向终点C运动,已知边BC的中点是点M,点P关于点M的对称点为点Q.当点P不与点M重合时,以MO为边在BC的上方作正方形MOEF,连结AC,设点P的运动时间为t秒,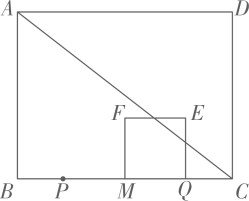 (1)、线段AB的长为 .(2)、用含t的代数式表示线段MQ的长.(3)、当点F恰好落在线段AC上时,求t的值.(4)、当正方形MOEF与△ACD重叠部分的图形是三角形时,直接写出t的取值范围.24. 在平面直角坐标系中,抛物线y=x2-2mx+1(m为常数)的图象与y轴交于点A.
(1)、线段AB的长为 .(2)、用含t的代数式表示线段MQ的长.(3)、当点F恰好落在线段AC上时,求t的值.(4)、当正方形MOEF与△ACD重叠部分的图形是三角形时,直接写出t的取值范围.24. 在平面直角坐标系中,抛物线y=x2-2mx+1(m为常数)的图象与y轴交于点A. (1)、求点A的坐标.(2)、当此抛物线的顶点恰好落在x轴的负半轴时,求此抛物线所对应的二次函数的表达式,并写出函数值y随x的增大而增大时x的取值范围.(3)、当xm时,若函数y=x2-2mx+1(m为常数)的最小值 , 求m的值.(4)、已知Rt△EFG三个顶点的坐标分别为E(m,m)、F(0,m),G(m,m-10).若|m|<10,设抛物线y=x2-2mx+1(m为常数)与△EFG的较短的直角边的交点为P,过点P作x轴的平行线,与抛物线的另一个交点为Q,过点A作x轴的平行线,与抛物线的另一个交点为B.若AB=2PQ,直接写出m的值,
(1)、求点A的坐标.(2)、当此抛物线的顶点恰好落在x轴的负半轴时,求此抛物线所对应的二次函数的表达式,并写出函数值y随x的增大而增大时x的取值范围.(3)、当xm时,若函数y=x2-2mx+1(m为常数)的最小值 , 求m的值.(4)、已知Rt△EFG三个顶点的坐标分别为E(m,m)、F(0,m),G(m,m-10).若|m|<10,设抛物线y=x2-2mx+1(m为常数)与△EFG的较短的直角边的交点为P,过点P作x轴的平行线,与抛物线的另一个交点为Q,过点A作x轴的平行线,与抛物线的另一个交点为B.若AB=2PQ,直接写出m的值,