江西省上饶市鄱阳县2022-2023学年八年级下学期3月月考数学试题
试卷更新日期:2023-04-03 类型:月考试卷
一、单选题
-
1. 若二次根式在实数范围内有意义,则x应满足的条件是( )A、 B、 C、 D、2. 由线段a,b,c组成的三角形是直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,3. 下列式子计算结果正确的是( )A、 B、 C、 D、4. 图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图所示的四边形 . 若 , 且 , 则的长度为( )
 A、 B、 C、4 D、5. 已知 , 则的值为( )A、 B、 C、2 D、46. “勾股树”是以正方形-边为斜边向外作直角三角形 ,再以该直角三角形的两直角边分别向外作正方形,重复这-过程所画出来的图形,因为重复数次后的形状好似--棵树而得名.假设下图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第五代勾股树中正方形的个数为( )
A、 B、 C、4 D、5. 已知 , 则的值为( )A、 B、 C、2 D、46. “勾股树”是以正方形-边为斜边向外作直角三角形 ,再以该直角三角形的两直角边分别向外作正方形,重复这-过程所画出来的图形,因为重复数次后的形状好似--棵树而得名.假设下图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第五代勾股树中正方形的个数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
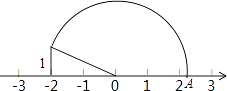
7. 化简:= .8. 如图,在数轴上点A表示的实数是 .
 9. 已知是整数,则正整数的最小值为 .10. 电流通过导线时会产生热量,电流,(单位:A)、导线电阻R(单位:Ω)、通电时间t(单位:s)与产生的热量Q(单位:J)满足 . 已知导线的电阻为8Ω,2s时间导线产生72J的热量,则I的值为A.11. 如图,正方体的棱长为3 cm,已知点B与点C间的距离为1 cm,一只蚂蚁沿着正方体的表面从点A爬到点C,需要爬行的最短距离为 .
9. 已知是整数,则正整数的最小值为 .10. 电流通过导线时会产生热量,电流,(单位:A)、导线电阻R(单位:Ω)、通电时间t(单位:s)与产生的热量Q(单位:J)满足 . 已知导线的电阻为8Ω,2s时间导线产生72J的热量,则I的值为A.11. 如图,正方体的棱长为3 cm,已知点B与点C间的距离为1 cm,一只蚂蚁沿着正方体的表面从点A爬到点C,需要爬行的最短距离为 . 12. 在中, , , , D是直线上的动点,若是等腰三角形,则的长度是 .
12. 在中, , , , D是直线上的动点,若是等腰三角形,则的长度是 .三、解答题
-
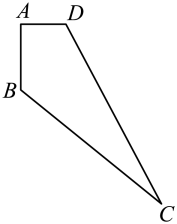
13.(1)、计算:(2)、计算: .14. 先化简,再求值: , 其中a=15. 随着3月12日植树节的到来,某企业计划对一块四边形空地进行绿化.如图,在四边形中, , 米,米,米,米,若每平方米绿化的费用为60元,请预计绿化的费用.
 16. 如图,在由的小正方形组成的网格中,每个小正方形的边长都是1,小正方形的 顶点叫格点.
16. 如图,在由的小正方形组成的网格中,每个小正方形的边长都是1,小正方形的 顶点叫格点.
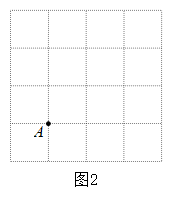 (1)、在图1中,以A为顶点,作一个三边长分别为2,和的格点三角形.(2)、在图2中,以A为顶点,作一个面积为的等腰直角三角形.17. 如图,长方形沿着对角线翻折,点C落在点处,与相交于点E,若 , , 求的长.
(1)、在图1中,以A为顶点,作一个三边长分别为2,和的格点三角形.(2)、在图2中,以A为顶点,作一个面积为的等腰直角三角形.17. 如图,长方形沿着对角线翻折,点C落在点处,与相交于点E,若 , , 求的长. 18. 如图1,在中, , .
18. 如图1,在中, , . (1)、求的面积.(2)、若P是边上的一点(不与点A,B重合),过点P作于点D,于点E,得到图2,移动点P的位置,的值会变化吗?若不变,求出的值;若变化,请说明理由.19. 下面是小华同学解答题目的过程,请认真阅读并完成相应任务.
(1)、求的面积.(2)、若P是边上的一点(不与点A,B重合),过点P作于点D,于点E,得到图2,移动点P的位置,的值会变化吗?若不变,求出的值;若变化,请说明理由.19. 下面是小华同学解答题目的过程,请认真阅读并完成相应任务.计算: .
解:原式第一步
第二步
第三步
(1)、任务一:以上步骤中,从第步开始出现错误,这一步错误的原因是 .(2)、任务二:请写出正确的计算过程.(3)、任务三:除纠正上述错误意外,请你根据平时的学习经验,就二次根式运算时还需注意的事项给其他同学提一条建议.20. “儿童散学归来早,忙趁东风放纸鸢.”如图,小明站在处,同时小亮在斜坡的处,且米,米, . (不考虑两人身高,点、、在同一水平线上) (1)、求小明与小亮之间的距离CD(结果保留根号).(2)、若风筝A在小明的北偏东方向上,且高度为60米, , 求此时风筝到小亮的距离 .21. 如图,在平面直角坐标系中, , 点P沿着从点A 向点B 运动若运动速度为 1个单位长度/秒,设点 P 的运动时间为t 秒.
(1)、求小明与小亮之间的距离CD(结果保留根号).(2)、若风筝A在小明的北偏东方向上,且高度为60米, , 求此时风筝到小亮的距离 .21. 如图,在平面直角坐标系中, , 点P沿着从点A 向点B 运动若运动速度为 1个单位长度/秒,设点 P 的运动时间为t 秒. (1)、若 ,
(1)、若 ,①线 , .
②点P的坐标为 .
(2)、连接 , 猜想 , , 之间的数量关系,并证明.22. 阅读下面解题过程.例:化简 .
解:
请回答下列问题.
(1)、归纳:请直接写出下列各式的结果:①=;
②= .
(2)、应用:化简(3)、拓展: . (用含n的式子表示,n为正整数)23. 课本再现(1)、如图1,四个全等的直角三角形拼成-一个大正方形,中间空白部分也是正方形.已知直角三角形的两直角边长分别为a,b,斜边长为c.课堂上,老师结合图形,用不同的方式表示大正方形的面积,证明了勾股定理.请证明: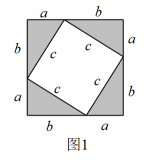 (2)、类比迁移:现将图1中的两个直角三角形向内翻折,得到图2,若 , , 则空白部分的面积为 .
(2)、类比迁移:现将图1中的两个直角三角形向内翻折,得到图2,若 , , 则空白部分的面积为 . (3)、方法运用:小贤将四个全等的直角三角形拼成图3的“帽子”形状,若 , , 请求出“帽子”外围轮廓(实线)的周长.
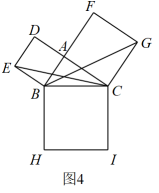
(3)、方法运用:小贤将四个全等的直角三角形拼成图3的“帽子”形状,若 , , 请求出“帽子”外围轮廓(实线)的周长.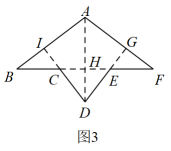 (4)、如图4,分别以的三条边向外作三个正方形,连接 , , 若设 , , , 则 , , 之间的关系为 .
(4)、如图4,分别以的三条边向外作三个正方形,连接 , , 若设 , , , 则 , , 之间的关系为 .