安徽省宿州市泗县2022-2023学年八年级下学期第一次数学质量调研
试卷更新日期:2023-04-03 类型:月考试卷
一、单选题
-
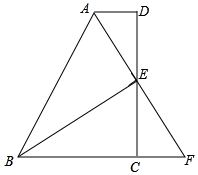
1. 判断两个直角三角形全等的方法错误的有( )A、两条直角边对应相等 B、斜边和一锐角对应相等 C、斜边和一条直角边对应相等 D、两个锐角对应相等2. 据气象台预报,2022年6月某日我区最高气温 , 最低气温 , 则当天气温的变化范围是( )A、 B、 C、 D、3. 如果 ,那么下列不等式正确的是( )A、 B、 C、 D、4. 下列给出的四组数中,能构成直角三角形三边的一组是( )A、 , , B、 , , C、 , , D、 , ,5. 若等腰三角形的两边长分别是3cm和5cm,则这个等腰三角形的周长是( )A、8cm B、13cm C、8cm或13cm D、11cm或13cm6. 如图,中,是边的高线,平分 , , , 则的面积是( )
 A、 B、 C、 D、7. 如图,中, , , . 为的角平分线,的长度为( )
A、 B、 C、 D、7. 如图,中, , , . 为的角平分线,的长度为( )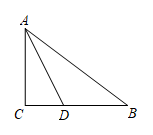 A、2 B、 C、3 D、8. 一次学校智力竞赛中共有道题,规定答对一题得分,答错或不答一道题扣分,得分为分以上可以获得奖品,小锋在本次竞赛中获得了奖品.假设小锋答对了题,可根据题意列出不等式( )A、 B、 C、 D、9. 用尺规作一个角的角平分线,下列作法中错误的是( )A、
A、2 B、 C、3 D、8. 一次学校智力竞赛中共有道题,规定答对一题得分,答错或不答一道题扣分,得分为分以上可以获得奖品,小锋在本次竞赛中获得了奖品.假设小锋答对了题,可根据题意列出不等式( )A、 B、 C、 D、9. 用尺规作一个角的角平分线,下列作法中错误的是( )A、 B、
B、 C、
C、 D、
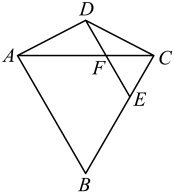
D、 10. 如图,已知△ABD是等边三角形, , E是AD上的点, , 与BD交于点F.则下列结论正确的有( )
10. 如图,已知△ABD是等边三角形, , E是AD上的点, , 与BD交于点F.则下列结论正确的有( )①连接AC,则AC垂直平分线段BD;②△DEF是等边三角形;③若 , 则;④若AB=8,DE=2,则CF=4.
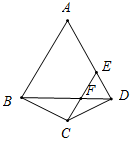 A、①② B、①②④ C、②③④ D、①③④
A、①② B、①②④ C、②③④ D、①③④二、填空题
-
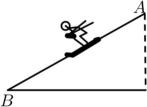
11. 如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑行至B,已知 , 则这名滑雪运动员的高度下降了米.
 12. 用“”或“”填空:若 , 则+1+1.13. 若代数式有意义,则实数x的取值范围是 .14. 已知点A()在第二象限角平分线上,则a的值是 .15. 如图, 平分 , , 的延长线交 于点E,若 ,则 的度数为 .
12. 用“”或“”填空:若 , 则+1+1.13. 若代数式有意义,则实数x的取值范围是 .14. 已知点A()在第二象限角平分线上,则a的值是 .15. 如图, 平分 , , 的延长线交 于点E,若 ,则 的度数为 . 16. 如图,四边形中, , , , , 其中 , 则四边形的面积是 .
16. 如图,四边形中, , , , , 其中 , 则四边形的面积是 .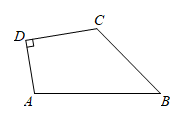 17. 如图,依据尺规作图的痕迹,求的度数°.
17. 如图,依据尺规作图的痕迹,求的度数°.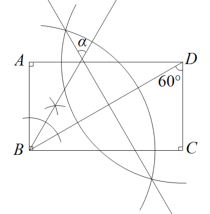 18. 如图,等边三角形ABC中,D、E分别为AB、BC边上的点, , AE与CD交于点F,于点G,则的度数为 .
18. 如图,等边三角形ABC中,D、E分别为AB、BC边上的点, , AE与CD交于点F,于点G,则的度数为 .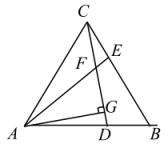
三、解答题
-
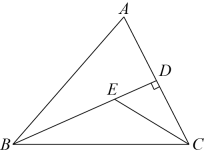
19. 如图,△ABC中,∠A=90°,∠B=60°,BC的垂直平分线交BC于点D,交AC于点E.

求证:
(1)、AE=DE;(2)、若AE=6,求CE的长.20. 如图,在中, . (1)、请用尺规作图法,在边上求作一点 , 使(保留作图痕迹,不要求写作法);(2)、连接 , 若 , , 求的长度.
(1)、请用尺规作图法,在边上求作一点 , 使(保留作图痕迹,不要求写作法);(2)、连接 , 若 , , 求的长度.