广东省茂名市高州十校联盟2022-2023学年七年级下学期第3周学情练习数学试题

试卷更新日期：2023-04-03 类型：月考试卷

进入出卷网下载

一、单选题

1. 一个正方体的平面展开图如图所示，将它折成正方体后，与汉字“冬”相对面上的汉字是（）

A、奥 B、林 C、匹 D、克

查看试题解析
2. 下列四个数中， $2023$ 的倒数是（）

A、 $2023$ B、 $- 2023$ C、 $\frac{1}{2023}$ D、 $- \frac{1}{2023}$

查看试题解析
3. 下列叙述中，正确的是（）

A、单项式 $x^{2} y$ 的系数是 $0$ ，次数是 $3$ B、多项式 $3 a^{3} b + 2 a^{2} + 1$ 是六次三项式 C、 $x^{m - 1} y$ 和 $\frac{1}{2} x^{2} y$ 是同类项，则 $m = 3$ D、 $π$ 、 $a$ 、 $0$ 、 $2^{2}$ 都是常数

查看试题解析
4. 如图， $O A$ 的方向是北偏东 $15 °$ ， $O B$ 的方向是北偏西 $40 °$ ，若 $O A$ 平分 $∠ B O C$ ，则 $∠ A O C$ 的度数为（）．

A、 $40 °$ B、 $55 °$ C、 $60 °$ D、 $70 °$

查看试题解析
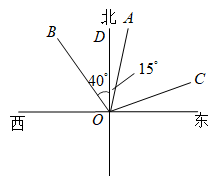5. 若关于 $x$ 的一元一次方程 $2 k - x - 4 = 0$ 的解是 $x = 2$ ，那么 $k$ 的值是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 在下列调查中，适宜采用普查的是（）

A、了解七（1）班学生校服的尺码情况 B、了解我省中学生的视力情况 C、检测一批电灯泡的使用寿命 D、调查《朗读者》的收视率

查看试题解析
7. 下列运算正确的是（）

A、 $a + 2 a^{2} = 3 a^{2}$ B、 $a^{3} \cdot a^{2} = a^{6}$ C、 ${(- x^{3})}^{2} = x^{6}$ D、 ${(x^{2})}^{3} = x^{5}$

查看试题解析
8. 纳米是非常小的长度单位，1纳米 $= 1 0^{- 9}$ 米，新型冠状病毒直径约为78纳米，用科学记数法表示该病毒的长度，下列结果正确的是（）

A、 $7.8 \times 1 0^{- 8}$ 米 B、 $7.8 \times 1 0^{- 9}$ 米 C、 $7.8 \times 1 0^{- 10}$ 米 D、 $78 \times 1 0^{- 8}$ 米

查看试题解析
9. 如图所示的运算程序中，若开始输入的 $x$ 值为 $24$ ，我们发现第 $1$ 次输出的结果为 $12$ ，第 $2$ 次输出的结果为 $6$ ， ……，则第2023次输出的结果为（）

A、 $6$ B、 $3$ C、 $24$ D、 $12$

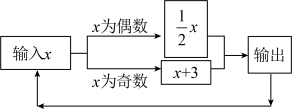查看试题解析
10. 如图，在一个由6个圆圈组成的三角形里，把1到6这6个数分别填入图的圆圈中，要求三角形的每条边上的三个数的和S都相等，那么S的最大值是（）

A、9 B、10 C、12 D、13

查看试题解析

二、填空题

11. 某日李老师登陆“学习强国” $A P P$ 显示为共有 $316900000$ 名用户在线， $316900000$ 这个数用科学记数法表示为 $3.169 \times 1 0^{n}$ ，此时 $n =$ ．

查看试题解析
12. 若3x＝4，3y＝5，则3^x+y= ．

查看试题解析
13. 将一张长方形纸片按如图所示的方式折叠， $B D$ 、 $B E$ 为折痕．若 $∠ A B E = 25 °$ ，则 $∠ D B C$ 为度．

查看试题解析
14. 计算 ${(- 0.25)}^{12} \times 4^{13}$ 的值是．

查看试题解析
15. 点 $C$ 是线段 $A B$ 上的三等分点， $D$ 是线段 $A C$ 的中点， $E$ 是线段 $B C$ 的中点，若 $C E = 2$ ，则 $A B$ 的长为．

查看试题解析

三、解答题

16. 计算：

(1)、 $7 - (+ 5) + (- 4) - (- 10)$ ；

(2)、 ${(- \frac{1}{2})}^{- 2} + {(- 1)}^{2033} + {(π - 3.14)}^{0} - | - 3 |$ ．

查看试题解析
17. 如图，是一个小正方体所搭几何体从上面看得到的平面图形，正方形中的数字表示在该位置小正方体的个数，请你画出它从正面和从左面看得到的平面图形．

查看试题解析
18. 解方程： $2 - \frac{x - 1}{2} = \frac{2 x + 1}{3} - x$

查看试题解析
19. 先化简，再求值： $- 8 m^{2} n + (m - n) (2 m + n) - 2 m n (- 3 m + 4 n) + 8 m n^{2}$ ，其中 ${(m + 2)}^{2} + | n - \frac{1}{2} | = 0$

查看试题解析
20. 某校组织全体学生开展汉字听写大赛，从中抽取部分学生成绩（得分为正整数，满分为100分）进行统计，绘制了两幅不完整的统计图，直方图从左至右分别对应A、B、C、D、E组，其中C组图象缺失．已知A组的频数比B组小48．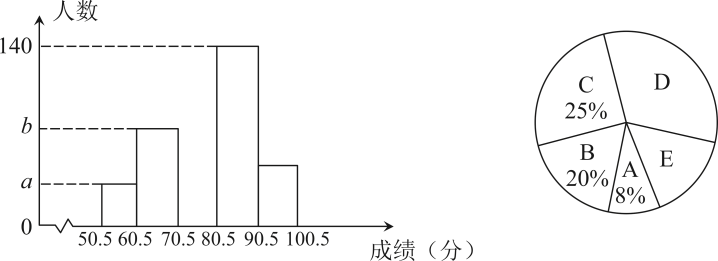
请你根据图中提供的信息解答下列问题：

(1)、求频数分布直方图中a、b的值；

(2)、扇形图中D部分扇形所对的圆心角的度数为；

(3)、若80分以上为优秀，全校共有1000名学生，估计成绩优秀的学生有多少名？

查看试题解析
21. 阅读下列材料：下面是底数大于1的数比较大小的两种方法．
①比较 $2^{a}$ ， $2^{b}$ 的大小；当 $a > b$ 时， $2^{a} > 2^{b}$ ， $∴$ 当同底数相同时，指数越大值越大；
②比较 $3^{50}$ 和 $2^{75}$ 的大小， $∵ 3^{50} = {(3^{2})}^{25} = 9^{25}$ ， $2^{75} = {(2^{3})}^{25} = 8^{25}$ ， $∵ 9 > 8$ ， $∴ 3^{50} > 2^{75}$ ．可以将其先化为同指数，再比较大小， $∴$ 指数相同时，底数越大值越大；
根据上述材料，回答下列问题．

(1)、比较大小 $3^{20}$ $9^{15}$ （填写>、<或=）；

(2)、已知 $a = 3^{55}$ ， $b = 4^{44}$ ， $c = 5^{33}$ ，试比较 $a$ 、 $b$ 、 $c$ 的大小．

查看试题解析
22. 列方程解应用题：某社区超市第一次用6000元购进甲、乙两种商品，其中甲商品的件数比乙商品件数的2倍少30件，甲、乙两种商品的进价和售价如表：

甲
乙
进价（元/件）
22
30
售价（元/件）
29
40

(1)、该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？

(2)、该超市第二次以第一次的进价又购进甲、乙两种商品，其中甲种商品的件数不变，乙种商品的件数是第一次的3倍；甲商品按原售价销售，乙商品在原售价上打折销售．第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多720元，求第二次乙种商品是按原价打几折销售？

查看试题解析
23. 如图，已知∠AOB=120°，射线OP从OA位置出发，以每秒2°的速度顺时针向射线OB旋转；与此同时，射线OQ以每秒6°的速度，从OB位置出发逆时针向射线OA旋转，到达射线OA后又以同样的速度顺时针返回，当射线OQ返回并与射线OP重合时，两条射线同时停止运动. 设旋转时间为t秒．

(1)、当t=2时，求∠POQ的度数；

(2)、当∠POQ=40°时，求t的值；

(3)、在旋转过程中，是否存在t的值，使得∠POQ= $\frac{1}{2}$ ∠AOQ？若存在，求出t的值；若不存在，请说明理由．

查看试题解析

	甲	乙
进价（元/件）	22	30
售价（元/件）	29	40