安徽省宿州市2022-2023学年七年下学期数学第一次月考试题

试卷更新日期：2023-04-03 类型：月考试卷

进入出卷网下载

一、单选题

1. 若 $2 \times 2^{2} \times 2^{n} = 2^{10}$ ，则 $n$ 等于（）

A、7 B、4 C、2 D、6

查看试题解析
2. 下列运算正确的是（）

A、 $3 a^{2} - a^{2} = 3$ B、 ${(a + b)}^{2} = a^{2} + b^{2}$ C、 ${(- 3 a b^{2})}^{2} = 9 a^{2} b^{4}$ D、 $a^{2} + a^{2} = a^{4}$

查看试题解析
3. 若 ${(a - 2023)}^{0} = 1$ 成立，则 $a$ 的值为（）

A、 $a \neq 0$ B、 $a \neq 2023$ C、 $a = 2023$ D、 $a = 0$ 或 $a = 2023$

查看试题解析
4. 石墨烯是目前世界上最薄的纳米材料，其理论厚度仅有0.00000000034m．这个数用科学记数法表示正确的是（）

A、 $3.4 \times 1 0^{- 9}$ B、 $0.34 \times 1 0^{- 9}$ C、 $3.4 \times 1 0^{- 10}$ D、 $3.4 \times 1 0^{- 12}$

查看试题解析
5. 有3张边长为a的正方形纸片，4张边长分别为a、b（b＞a）的矩形纸片，5张边长为b的正方形纸片，从其中取出若干张纸片，每种纸片至少取一张，把取出的这些纸片拼成一个正方形（按原纸张进行无空隙、无重叠拼接），则拼成的正方形的边长最长可以为（）

A、a+b B、2a+b C、3a+b D、a+2b

查看试题解析
6. 下列各式：①（a-b）（b+a） ②（a-b）（-a-b） ③（-a-b）（a+b） ④（a-b）（-a+b），能用于平方差公式计算的有（）

A、1 个 B、2 个 C、3 个 D、4 个

查看试题解析
7. 如图，长为 $a$ ，宽为 $b$ 的长方形的周长为16，面积为12，则 $a^{2} + b^{2}$ 的值为（）

A、88 B、70 C、64 D、40

查看试题解析
8. 已知， $a = 2^{55}$ ， $b = 3^{44}$ ， $c = 4^{33}$ ，则a、b、c的大小关系是（）

A、 $b > c > a$ B、 $a > b > c$ C、 $c > a > b$ D、 $c > b > a$

查看试题解析
9. 若 $(3 x + 4) (x + p) = m x^{2} + n x - 12$ ，则下列结论正确的是（）

A、 $m = 12$ B、 $n = 5$ C、 $p = 3$ D、 $m n p = 45$

查看试题解析
10. 在数学中，为了书写简便，18世纪数学家欧拉就引进了求和符号“ $\sum$ ”．如：记 $\sum_{k = 1} k = 1 + 2 + 3 + \cdot \cdot \cdot + (n - 1) + n$ ； $\sum_{k = 1} (x + k) = (x + 1) + (x + 2) + \cdot \cdot \cdot + (x + n)$ ．已知 $\sum_{k = 1} [(x + k) (x - k + 1)] = 4 x^{2} + 4 x + m$ ，则 $m$ 的值是（）

A、 $20$ B、 $- 70$ C、 $- 40$ D、 $- 20$

查看试题解析

二、填空题

11. 若 $3^{x} = 5$ ， $9^{y} = 7$ ，则 $3^{x + 2 y}$ 的值为．

查看试题解析
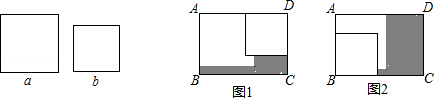
12. 若一个三角形的面积为 $x^{3} y - 3 x^{2}$ ，它的一条边长为 $2 x^{2}$ ，则这条边上的高为．

查看试题解析
13. 已知 $x^{2} + 4 m x + 36$ 是完全平方式，则 $m$ 的值为．

查看试题解析
14. 在长方形ABCD内，将两张边长分别为a和b（a＞b）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），长方形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S₁ ，图2中阴影部分的面积为S₂ ．当AD﹣AB=2时，S₂﹣S₁的值为．（用a、b的代数式表示）

查看试题解析

三、解答题

15. 计算： $- 2^{2} + {(π - 2023)}^{0} - {(- \frac{1}{2})}^{- 1}$ ．

查看试题解析
16. 先化简，再求值： $(x + y) (x - y) - {(x + 2 y)}^{2} + 15 x^{2} y^{4} \div 3 x^{2} y^{2}$ ，其中 $x = 3$ ， $y = - 1$ ．

查看试题解析
17. 已知 $a^{m} = 6$ ， $a^{n} = 4$ ，求 $a^{2 m - n}$ 的值．

查看试题解析
18. 从前，古希腊的一位庄园主人把一块边长为 $a m (a > 8)$ 的正方形土地租给租户约翰，第二年，他对约翰说：“我把这块地的一边增加 $8 m$ ，相邻的另一边减少 $8 m$ ，变形矩形土地继续租给你，租金不变，你也没有吃亏，你看如何？”若是这样，你觉得约翰吃亏了吗？通过计算说明你的结论．

查看试题解析
19. 某同学在计算一个多项式除以 $- 3 x^{2}$ 时，因抄错运算符号，算成了加上 $- 3 x^{2}$ ，得到的结果是 $6 x^{3} - 6 x^{2}$ ，那么原题正确的计算结果是多少？

查看试题解析
20. 根据现有的知识，当 $1 0^{a} = 200$ ， $1 0^{b} = \frac{1}{5}$ 时，不能分别求出 $a$ 和 $b$ 的值，但是小红却利用它们求出了 $4^{a} \div 2^{2 b}$ 的值，你知道她是怎样计算的吗？请写出计算过程．

查看试题解析
21. 小明使用比较简便的方法完成了一道作业题，如下框：
小明的作业
计算： $8^{5} \times {(- 0.125)}^{5}$ ．
解： $8^{5} \times {(- 0.125)}^{5}$
$= {(- 8 \times 0.125)}^{5}$
$= {(- 1)}^{5}$
$= - 1$ ．
请你参考小明的方法解答下列问题．
计算：

(1)、 $4^{2023} \times {(- 0.25)}^{2023}$ ；

(2)、 ${(\frac{12}{5})}^{2021} \times {(- \frac{5}{6})}^{2023} \times {(\frac{1}{2})}^{2022}$ ．

查看试题解析
22. 我们规定： $a^{- p} = \frac{1}{a^{p}} (a \neq 0)$ ，即 $a$ 的负 $p$ 次幂等于 $a$ 的 $p$ 次幂的倒数．例： $4^{- 2} = \frac{1}{4^{2}}$ ．

(1)、计算： ${(- 2)}^{- 2} =$ ；若 $2^{- p} = \frac{1}{8}$ ，则 $p =$ ；

(2)、若 $a^{- 2} = \frac{1}{16}$ ，求 $a$ 的值；

(3)、若 $a^{- p} = \frac{1}{9}$ ，且 $a$ ， $p$ 为整数，求满足条件的 $a$ ， $p$ 的值．

查看试题解析
23. 数形结合是解决数学问题的一种重要的思想方法，借助图的直观性，可以帮助理解数学问题．

(1)、请写出图1，图2，图3阴影部分的面积分别能解释的乘法公式．
图1：，图2：，图3：；

(2)、用4个全等的长和宽分别为 $a$ ， $b$ 的长方形拼摆成一个如图4的正方形，请你通过计算阴影部分的面积，直接写出这三个代数式 ${(a + b)}^{2}$ ， ${(a - b)}^{2}$ ， $a b$ 之间的等量关系；

(3)、根据（1），（2）中你探索发现的结论，完成下列计算：
已知 $a - b = 5$ ， $a b = - 4$ ，求代数式① $a^{2} + b^{2}$ ；② $a + b$ 的值．

查看试题解析