2023年浙教版数学七年级下册全方位训练卷第五章分式（进阶版）

试卷更新日期：2023-04-01 类型：单元试卷

进入出卷网下载

一、单选题（每题2分，共20分）

1. 对于非负整数x，使得 $\frac{x^{2} + 3}{x + 3}$ 是一个正整数，则符合条件x的个数有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
2. 对于分式 $\frac{| x | - 2}{x + 2}$ ，下列说法正确的是（）

A、当x＝﹣2时分式有意义 B、当x＝±2时分式的值为零 C、当x＝0时分式无意义 D、当x＝2时分式的值为零

查看试题解析
3. 若分式 $\frac{x^{2}}{x^{2} + x}$ 化简为 $\frac{x}{x + 1}$ ，则 $x$ 应满足的条件是（）

A、 $x \neq 1$ 或 $x \neq 0$ B、 $x \neq - 1$ 且 $x \neq 0$ C、 $x \neq - 1$ D、 $x \neq 0$

查看试题解析
4. 下列说法正确的是（）

A、分式 $\frac{x^{2} - 4}{x - 2}$ 的值为零，则 $x$ 的值为±2 B、根据分式的基本性质， $\frac{m}{n}$ 可以变形为 $\frac{m x^{2}}{n x^{2}}$ C、分式 $\frac{x y}{3 x - 2 y}$ 中的 $x ， y$ 都扩大3倍，分式的值不变 D、分式 $\frac{x + 1}{x^{2} + 1}$ 是最简分式

查看试题解析
5. 下列各式中，计算结果正确的有（）
⑴ $\frac{3 x}{x^{2}} \cdot \frac{x}{3 x} = \frac{1}{x}$ （2） $a \div b \times \frac{1}{b} = a$ （3） $\frac{a}{a^{2} - 1} \div \frac{a^{2}}{a^{2} + a} = \frac{1}{a - 1}$ （4） $8 a^{2} b^{2} \div (- \frac{3 a}{4 b^{2}}) = - 6 a^{3} b$ ⑸ $\frac{1}{c} + \frac{2}{c} = \frac{3}{c}$ （6） $\frac{0.2 a + b}{0.7 a - b} = \frac{2 a + b}{7 a - b}$

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 已知 $x$ ， $y$ 为整数，且满足 $(\frac{1}{x} + \frac{1}{y}) (\frac{1}{x^{2}} + \frac{1}{y^{2}}) = - \frac{2}{3} (\frac{1}{x^{4}} - \frac{1}{y^{4}})$ ，则 $x + y$ 的可能的值有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 某数学老师模仿学生喜欢的《王牌对王牌》节目在课堂上设计了一个接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算得到结果，再将计算结果传递给下一人，最后完成化简．过程如图所示，接力中，自己负责的那一步出现错误的是（）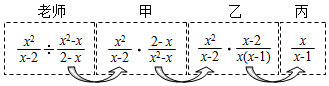

A、只有乙 B、只有丙 C、甲和丙 D、乙和丙

查看试题解析
8. 甲、乙两人分两次在同一粮店内买粮食，两次的单价不同，甲每次购粮100千克，乙每次购粮100元．若规定：谁两次购粮的平均单价低，谁的购粮方式就合算．那么这两次购粮（）

A、甲合算 B、乙合算 C、甲、乙一样 D、无法确定

查看试题解析
9. 商家常将单价不同的A，B两种糖混合成“什锦糖”出售，记“什锦糖”的单价为：A，B两种糖的总价与A，B两种糖的总质量的比．现有两种“什锦糖”：一种是由相同千克数的A种糖和B种糖混合而成的“什锦糖”甲，另一种是由相同金额数的A种糖和B种糖混合而成的“什锦糖”乙．若B种糖比A种糖的单价贵40元/千克，“什锦糖”甲比“什锦糖”乙的单价贵5元/千克，则A种糖的单价为（）

A、50元/千克 B、60元/千克 C、70元/千克 D、80元/千克

查看试题解析
10. 甲、乙两人同时从圆形跑道（圆形跑道的总长小于700m）上一直径两端A，B相向起跑．第一次相遇时离A点100m，第二次相遇时离B点60m，则圆形跑道的总长为（）

A、240m B、360m C、480m D、600m

查看试题解析

二、填空题（每空3分，共21分）

11. 已知 $\frac{x}{x^{2} - x + 1}$ ＝ $\frac{1}{7}$ ，则 $\frac{x^{2}}{x^{4} - x^{2} + 1}$ ＝．

查看试题解析
12. 计算 $\frac{4 y^{2} - x^{2}}{x^{2} + 2 x y + y^{2}} \div \frac{x - 2 y}{2 x^{2} + 2 x y} =$ .

查看试题解析
13. 有一个分式，三位同学分别说出了它的一些特点，甲：分式的值不可能为0；乙：分式有意义时的取值范围是≠±1；丙：当=-2时，分式的值为1.请你写出满足上述全部特点的一个分式：.

查看试题解析
14. 不改变分式的值，将分式的分子、分母的各项系数都化为整数，则 $\frac{a - \frac{2}{3} b}{\frac{1}{2} + 2 b}$ ＝．

查看试题解析
15. 欧拉是18世纪瑞士著名的数学家，他的贡献不仅遍及高等数学的各个领域，在初等数学中也留下了他的足迹．下面是关于分式的欧拉公式：
$\frac{a^{r}}{(a - b) (a - c)} + \frac{b^{r}}{(b - c) (b - a)} + \frac{c^{r}}{(c - a) (c - b)} = {\begin{cases} p ， & r = 0 时 \\ 0 ， & r = 1 时 \\ 1 ， & r = 2 时 \\ a + b + c ， & r = 3 时 \end{cases}$

（其中a，b，c均不为零，且两两互不相等）．

(1)、当 $r = 0$ 时，常数p的值为．

(2)、利用欧拉公式计算： $\frac{202 2^{3}}{2} - 202 1^{3} + \frac{202 0^{3}}{2} =$ ．

查看试题解析
16. 某次列车平均提速 $v km / h$ ，用相同的时间，列车提速前行驶 $s km$ ，提速后比提速前多行驶 $50 m$ .设提速前列车的平均速度是 $x km / h$ .根据题意分别列出下列四个方程：① $\frac{s}{x} = \frac{s + 50}{x + v}$ ；② $\frac{s}{x + v} = \frac{s + 50}{x}$ ；③ $\frac{x}{x + v} = \frac{s}{s + 50}$ ；④ $\frac{s}{x} = \frac{50}{v}$ .则其中正确的方程有.(填序号)

查看试题解析

三、计算题（共3题，共20分）

17. 计算.

(1)、 $\frac{1}{x} - \frac{x}{x + 1} - \frac{x}{x^{2} + x}$ ；

(2)、 $\frac{x^{2} - 4 x + 4}{x^{2} - 4} + \frac{x - 2}{x^{2} + 2 x} + 2$ ；

(3)、 $x + 2 y + \frac{4 y^{2}}{x - 2 y} - \frac{4 x^{2} y}{x^{2} - 4 y^{2}}$ .

查看试题解析
18. 解分式方程：

(1)、 $\frac{2}{x + 3} = \frac{1}{x - 2}$ ；

(2)、 $\frac{x + 5}{x - 5} = 1 + \frac{10}{x^{2} - 10 x + 25}$ .

查看试题解析
19. 化简： $\frac{1}{x (x + 1)} + \frac{1}{(x + 1) (x + 2)} + \frac{1}{(x + 2) (x + 3)} +$ $\frac{1}{(x + 3) (x + 4)}$ .

查看试题解析

四、解答题（共6题，共59分）

20. 从三个整式；① $a^{2} - 2 a b + b^{2}$ ，② $3 a - 3 b$ ，③ $a^{2} - b^{2}$ 中，任意选择两个分别作为一个分式的分子和分母．

(1)、一共能得到个不同的分式；

(2)、这些分式化简后结果为整式的分式有哪些？并写出化简结果．

查看试题解析
21. 某快递公司有甲、乙、丙三个机器人分配快件，甲单独完成需要x小时，乙单独完成需要y小时，丙单独完成需要z小时．

(1)、求甲单独完成的时间是乙丙合作完成时间的几倍？

(2)、若甲单独完成的时间是乙丙合作完成时间的a倍，乙单独完成的时间是甲丙合作完成时间的b倍，丙单独完成的时间是甲乙合作完成时间的c倍，求 $\frac{1}{a + 1} + \frac{1}{b + 1} + \frac{1}{c + 1}$ 的值．

查看试题解析
22. 阅读材料：在处理分数和分式的问题时，有时由于分子大于分母，或分子的次数高于分母的次数，在实际运算时难度较大，这时，我们可将分数（分式）拆分成一个整数（整式）与一个真分数（真分式）的和（差）的形式，通过对它的简单分析来解决问题，我们称这种方法为分离常数法，此法在处理分式或整除问题时颇为有效.
将分式分离常数可类比假分数变形带分数的方法进行，如： $\frac{x^{2} - 2 x + 3}{x - 1} = \frac{x (x - 1) + x - 2 x + 3}{x - 1} = x +$ $\frac{- (x - 1) + 2}{x - 1} = x - 1 + \frac{2}{x - 1}$ ，这样，分式就拆分成一个分式 $\frac{2}{x - 1}$ 与一个整式 $x - 1$ 的和的形式.

根据以上阅读材料，解答下列问题：

(1)、若x为整数， $\frac{x + 6}{x + 4}$ 为负整数，可求得 x最大值= ；

(2)、利用分离常数法，求分式 $\frac{2 x^{2} + 5}{x^{2} + 1}$ 的取值范围；

(3)、若分式 $\frac{5 x^{2} + 9 x - 3}{x + 2}$ 拆分成一个整式与一个真分式（分子为整数）的和（差）的形式为： $5 m - 11 + \frac{1}{n - 6}$ （整式部分对应等于 $5 m - 11$ ，真分式部分对应等于 $\frac{1}{n - 6}$ ）.
①用含x的式子表示出mn；

②随着x的变化， $m^{2} + n^{2} + m n$ 有无最小值？如有，最小值为多少？

查看试题解析
23. 阅读下列解题过程：
已知 $\frac{x}{x^{2} + 1} = \frac{1}{3}$ ，求 $\frac{x^{2}}{x^{4} + 1}$ 的值.

解：由 $\frac{x}{x^{2} + 1} = \frac{1}{3}$ ，知 $x \neq 0$ ，所以 $\frac{x^{2} + 1}{x} = 3$ ，即 $x + \frac{1}{x} = 3$ .

∴ $\frac{x^{4} + 1}{x^{2}} = x^{2} + \frac{1}{x^{2}} = {(x + \frac{1}{x})}^{2} - 2 = 3^{2} - 2 = 7$

∴ $\frac{x^{2}}{x^{4} + 1}$ 的值为7的倒数，即 $\frac{1}{7}$ .

以上解法中先将已知等式的两边“取倒数”，然后求出待求式子倒数的值，我们把此题的这种解法叫做“倒数法”，请你利用“倒数法”解决下面问题：

(1)、已知 $\frac{x}{x^{2} + 1} = \frac{1}{2}$ ，求 $\frac{x^{2}}{x^{4} + 1}$ 的值.

(2)、已知 $\frac{x}{x^{2} - x + 1} = \frac{1}{7}$ ，求 $\frac{x^{2}}{x^{4} - x^{2} + 1}$ 的值.

(3)、已知 $\frac{x y}{x + y} = 2$ ， $\frac{y z}{y + z} = \frac{4}{3}$ ， $\frac{z x}{z + x} = \frac{4}{3}$ ，求 $\frac{x y z}{x y + y z + z x}$ 的值.

查看试题解析
24. 小红到离家2100米的学校参加艺术节联欢会，到学校时发现演出道具忘在家中，此时距联欢会开始还有45分钟，于是她马上步行回家取道具，随后骑自行车返回学校.已知小红骑自行车到学校比她从学校步行到家用时少20分钟，且骑自行车的平均速度是步行平均速度的3倍.

(1)、小红步行的平均速度（单位：米/分）是多少？

(2)、小红能否在联欢会开始前赶到学校？（通过计算说明你的理由）

查看试题解析
25. 用如图所示的甲、乙、丙三块木板做一个长、宽、高分别为a厘米，b厘米和10厘米的长方体木箱，其中甲块木板锯成两块刚好能做箱底和一个长侧面，乙块木板刚好能做一个长侧面和一个短侧面，丙块木板刚好能做一个箱盖和剩下的一个短侧面（厚度忽略不计，a＞b）

(1)、用含a，b的代数式分别表示这三块木板的面积.

(2)、若甲块木板的面积比丙块木板的面积大200平方厘米，木箱的体积为150000立方厘米，求乙块木板的面积.

(3)、如果购买一块长为100厘米，宽为（a+b）厘米的长方形木板做这个木箱，木板的利用率为90%，试求分式 $\frac{5}{a} + \frac{5}{b}$ + $\frac{a^{2} b - a b^{2}}{7 a^{2} - 7 b^{2}}$ 的值.

查看试题解析

2023年浙教版数学七年级下册全方位训练卷第五章 分式（进阶版）

一、单选题（每题2分，共20分）

二、填空题（每空3分，共21分）

三、计算题（共3题，共20分）

四、解答题（共6题，共59分）

2023年浙教版数学七年级下册全方位训练卷第五章分式（进阶版）