2023年浙教版数学七年级下册全方位训练卷5.4分式的加减法

试卷更新日期：2023-04-01 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列运算正确的是（）

A、 $\frac{1}{2 a} + \frac{1}{a} = \frac{2}{3 a}$ B、 $\frac{1}{a - 1} - \frac{1}{a + 1} = \frac{2}{a^{2} - 1}$ C、 $\frac{3 b}{4 a} \cdot \frac{2 a}{9 b^{2}} = \frac{b}{6}$ D、 $\frac{1}{3 a b} \div \frac{2 b^{2}}{3 a} = \frac{b^{3}}{2}$

查看试题解析
2. 化简 $(9 - x^{2}) \div \frac{x^{2} - 3 x}{x}$ 的结果是（）

A、 $x + 3$ B、 $- x - 3$ C、 $\frac{1}{x + 3}$ D、 $- \frac{1}{x + 3}$

查看试题解析
3. 若分式 $\frac{x^{2}}{x - 1} □ \frac{x}{x - 1} = x$ 则在“ $□$ ”处的运算符号（）

A、只能是“ $\div$ ” B、可以是“ $\div$ ”或“ $-$ ” C、不能是“ $-$ ” D、可以是“ $\times$ ”或“ $+$ ”

查看试题解析
4. 若x是非负整数，则表示 $\frac{2 x}{x + 2} - \frac{x^{2} - 4}{(x + 2)^{2}}$ 的值的对应点落在如图数轴上的范围是（）

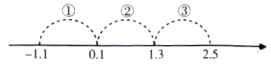A、① B、② C、③ D、①或②

查看试题解析
5. 分式 $\frac{1}{2 m + 2}$ 与 $\frac{1}{m + 1}$ 的最简公分母是（）

A、 $2 m + 2$ B、 $m + 2$ C、 $m + 1$ D、 $m^{2} - 1$

查看试题解析
6. 已知 $\frac{1}{x} + \frac{1}{y + z} = \frac{1}{2}$ ， $\frac{1}{y} + \frac{1}{z + x} = \frac{1}{3}$ ， $\frac{1}{z} + \frac{1}{x + y} = \frac{1}{4}$ ，则 $\frac{2}{x} + \frac{3}{y} + \frac{4}{z}$ 的值为（）

A、1 B、 $\frac{3}{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析
7. 若 $a$ ， $b$ 为实数且满足 $a \neq - 1$ ， $b \neq - 1$ ，设 $M = \frac{a}{a + 1} + \frac{b}{b + 1}$ ， $N = \frac{1}{a + 1} + \frac{1}{b + 1}$ ，有以下2个结论： $①$ 若 $a b = l$ ，则 $M = N$ ； $②$ 若 $a + b = 0$ ，则 $M N \leq 0 .$ 下列判断正确的是（）

A、①对②错 B、①错②对 C、①②都错 D、①②都对

查看试题解析
8. 已知 $a > 1$ ， $A = \frac{a}{a - 1}$ ， $B = \frac{a - 1}{a}$ ， $C = \frac{a}{a + 1}$ ，则 $A$ 、 $B$ 、 $C$ 的大小关系是（）

A、 $A > C > B$ B、 $A > B > C$ C、 $C > B > A$ D、 $C > A > B$

查看试题解析
9. 当分式 $- \frac{1}{x y}$ 与 $- \frac{1}{x^{2} y}$ 经过计算后的结果是 $- \frac{x + 1}{x^{2} y}$ 时，则它们进行的运算是（）

A、分式的加法 B、分式的减法 C、分式的乘法 D、分式的除法

查看试题解析

10. 如图是佳佳计算

\frac{x - 3}{x^{2} - 4} + \frac{1}{2 - x}

的过程，则下列说法中正确的是（）

$\frac{x - 3}{x^{2} - 4} + \frac{1}{2 - x}$

$= \frac{x - 3}{(x + 2) (x - 2)} - \frac{1}{x - 2}$ ①

$= \frac{x - 3}{(x + 2) (x - 2)} - \frac{x + 2}{(x + 2) (x - 2)}$ ②

$= x - 3 - x - 2$ ③

$= - 5$ ④

A、运算完全正确 B、第①②两步都有错 C、只有第③步有错 D、第②③两步都有错

查看试题解析

二、填空题（每空3分，共27分）

11. 计算： $\frac{2}{x - 3} - \frac{12}{x^{2} - 9} =$ ．

查看试题解析
12. 已知 $m + n = 2 ， m n = - 1$ ，则 $\frac{m + 1}{n} + \frac{n + 1}{m}$ ＝．

查看试题解析
13. 一组按规律排列的式子： $- \frac{b^{2}}{a}$ ， $\frac{b^{5}}{a^{2}}$ ， $- \frac{b^{8}}{a^{3}}$ ， $\frac{b^{11}}{a^{4}}$ ，…（ab≠0），其中第7个式子是，第n个式子是（n为正整数）．

查看试题解析
14. 分式 $\frac{1}{- a^{2} + 1} ， \frac{1}{a^{2} + a}$ 的最简公分母是， $\frac{1}{- a^{2} + 1} + \frac{1}{a^{2} + a}$ =

查看试题解析
15. 学习了“分式的加法”的相关知识后，小明同学画出了如图：请问他画的图中①为， ②为．

查看试题解析
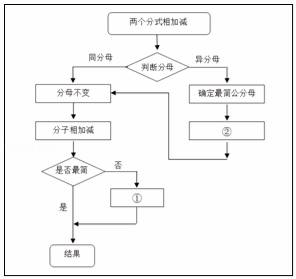16. 定义：如果一个分式能化成一个整式与一个分子为常数的分式的和的形式，则称这个分式为“和谐分式”.如： $\frac{x + 1}{x - 1} = \frac{x - 1 + 2}{x - 1} = \frac{x - 1}{x - 1} + \frac{2}{x - 1} = 1 + \frac{2}{x - 1}$ ，则 $\frac{x + 1}{x - 1}$ 是“和谐分式”.同时我们也可以将“和谐分式化成一个整式与一个分子为常数的分式的和的形式，如： $\frac{a^{2} - 2 a + 3}{a - 1} = a - 1 + \frac{2}{a - 1}$ ，那么若分式： $\frac{3 x + 6}{x + 1} - \frac{x - 1}{x} \div \frac{x^{2} - 1}{x^{2} + 2 x}$ 的值为整数.则整数x取值为：.

查看试题解析

三、计算题（共5题，共39分）

17. 计算：

(1)、 $\frac{3}{2 a} + \frac{1}{a^{2}}$

(2)、 $\frac{x^{2} y^{5}}{2 a^{2} b^{3}} \div \frac{x y^{3}}{4 a b}$

(3)、 $(\frac{b}{a^{3}}) \times {(\frac{b}{a})}^{- 4} \div {(- \frac{a}{b})}^{2}$

(4)、 $\frac{4 a + 4}{a^{2} - 4} - \frac{1}{2 + a}$

查看试题解析
18. 计算： $(\frac{1}{a + b} + \frac{1}{a - b} - \frac{1}{a^{2} - b^{2}}) \div \frac{1}{a^{2} - b^{2}}$ .

查看试题解析
19. 已知 $a + b = 1$ ， $a b = - 3$ .求下列代数式的值：

(1)、 $\frac{a}{b} + \frac{b}{a}$ ；

(2)、 $\frac{1}{a^{2} - 3} + \frac{1}{b^{2} - 3}$ .

查看试题解析
20. 先化简，再求值.

(1)、 $\frac{a^{2} - 2 a b + b^{2}}{a^{2} - b^{2}} + \frac{b}{a + b}$ ，其中 $a = - 2 ， b = 1$ ；

(2)、 $\frac{x^{2} - 9}{x - 1} \div \frac{x^{2} + 3 x}{x - 1} + \frac{4}{x}$ ，其中 $x = 2$ .

查看试题解析
21. 先化简，后求值： $(\frac{x^{2} - 1}{x^{2} + 2 x + 1} - 1) \div \frac{x - 1}{x + 1}$ ，其中 $x$ 的值从 $- 1$ ， $0$ ， $1$ ， $2$ 中选一个合适的数．

查看试题解析

四、解答题（共3题，共24分）

22. 以下是圆圆计算 $\frac{x^{2}}{x - 1} + \frac{1}{1 - x}$ 的解答过程.
解： $\frac{x^{2}}{x - 1} + \frac{1}{1 - x} = \frac{x^{2}}{x - 1} + \frac{1}{x - 1} = \frac{x^{2} + 1}{x - 1}$ .
圆圆的解答过程是否有错误？如果有错误，写出正确的解答过程.

查看试题解析
23. 从甲地到乙地有两条路，每条路都有6km，其中第一条路是平路，第二条路有3km的上坡路﹐3km的下坡路.小丽在上坡路上的骑车速度为vkm/h，在平路上的骑车速度为2vkm/h，在下坡路上的骑车速度为3ukm/h.

(1)、当走第二条路时，她从甲地到乙地需要多长时间?

(2)、她走哪条路花费的时间少?少多长时间?

查看试题解析
24. 我们规定：分式中，在分子、分母都是整式的情况下，如果分子的次数低于分母的次数，称这样的分式为真分式．例如，分式 $\frac{4}{x + 2}$ ， $\frac{3 x^{2}}{x^{3} － 4 x}$ 是真分式．如果分子的次数不低于分母的次数，称这样的分式为假分式．例如，分式 $\frac{x + 1}{x － 1}$ ， $\frac{x^{2}}{x + 1}$ 是假分式．一个假分式可以化为一个整式与一个真分式的和．例如， $\frac{x + 1}{x － 1}$ = $\frac{(x - 1) + 2}{x － 1}$ =1＋ $\frac{2}{x － 1}$ ， $\frac{2 x - 3}{x + 1}$ = $\frac{2 x + 2 - 5}{x + 1}$ = $\frac{2 x + 2}{x + 1}$ + $\frac{- 5}{x + 1}$ = 2＋ $\frac{- 5}{x + 1}$ ．

(1)、将假分式 $\frac{4 x － 5}{x + 1}$ 化为一个整式与一个真分式的和；

(2)、将假分式 $\frac{a^{2} － 4 a + 6}{a － 1}$ 化成一个整式与一个真分式的和的形式为： $\frac{a^{2} － 4 a + 6}{a － 1}$ = a＋m＋ $\frac{n}{a － 1}$ ，求m、n的值；并直接写出当整数a为何值时，分式 $\frac{a^{2} － 4 a + 6}{a － 1}$ 为正整数；

(3)、自然数A是 $\frac{10^{18} + 2022}{10^{9} + 2}$ 的整数部分，则A的数字和为．（把组成一个数的各个数位上的数字相加，所得的和，就叫做这个数的数字和．例如：126的数字和就是1+2+6=9）

查看试题解析