2023年浙教版七年级下学期数学期中模拟卷（4）

试卷更新日期：2023-04-01 类型：期中考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图， $A B ∥ C D$ ， $D E ∥ C B$ ， $∠ B = 35 °$ ，则 $∠ D =$ （）

A、 $145 °$ B、 $150 °$ C、 $120 °$ D、 $165 °$

查看试题解析
2. 下列运算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $a^{8} \div a^{5} = a^{3}$ C、 $a^{2} \cdot a^{2} = 2 a^{2}$ D、 ${(- a^{2})}^{3} = a^{6}$

查看试题解析
3. 已知 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是方程 $m x - y = 4$ 的一个解，则 $m$ 的值为（）

A、5 B、6 C、7 D、8

查看试题解析
4. 一个长方形的长为2x﹣y，宽为2x+y，则这个长方形的面积是（）

A、4x²﹣y² B、4x²+y² C、2x²﹣y² D、2x²+y²

查看试题解析
5. 如图，下列条件中，不能判断直线 $l_{1} ∥ l_{2}$ 的是（）

A、∠1=∠2 B、∠3=∠4 C、∠4=∠6 D、∠2＋∠5=180°

查看试题解析
6. 将含30°的直角三角板与直尺如图所示放置，若∠2=40°，则∠1的度数为（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
7. 已知 $a = (- 0.2)^{0}$ ， $b = - 2^{- 1}$ ， $c = {(- \frac{1}{2})}^{- 2}$ ，比较 $a$ ， $b$ ， $c$ 的大小（）

A、 $a < b < c$ B、 $b < c < a$ C、 $a < c < b$ D、 $b < a < c$

查看试题解析
8. 若x+m与x﹣5的乘积中不含x的一次项，则m的值是（）

A、﹣5 B、0 C、1 D、5

查看试题解析
9. 解方程组 ${\begin{array}{l} 2 x + 3 y = 8 ， \\ 3 x - 2 y = - 1 \end{array}$ 的思路可用如图的框图表示，圈中应填写的对方程①②所做的变形为（）

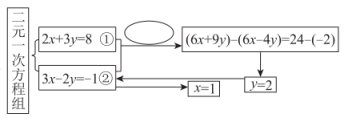A、①×2+②×3 B、①×2-②×3 C、①×3-②×2 D、①×3+②×2

查看试题解析
10. 如图，Rt△BCE中，∠BCE＝90°，点C是线段BG上的一点，设BC=a，CG=CE=b，以BC、CE为边向两边作正方形，面积分别是S₁和S₂ ，两正方形的面积和S₁＋S₂＝40，已知BG＝8，则阴影部分的面积为（）

A、6 B、8 C、12 D、16

查看试题解析

二、填空题（每空3分，共30分）

11. 小明同学在百度搜索引擎中输入“中国梦，我的梦”，引擎搜索耗时0.000175秒，将这个数字用科学记数法表示为.

查看试题解析
12. 若方程 $2 x^{m - 1} + y^{2 n + m} = \frac{1}{2}$ 是二元一次方程，则 $m n =$ .

查看试题解析
13. 计算（-2a²）³÷a³的结果是．

查看试题解析
14. 若 $3^{m} = 2$ ， $9^{n} = 10$ ，则 $3^{m + 2 n} =$ ．

查看试题解析
15. 若 $ 2 x^{5} y^{2 m + 3 n}$ 与 $ - 3 x^{3 m + 2 n} y^{6}$ 是同类项，则 $| m - n | =$ ．

查看试题解析
16. 如图，BA∥DE，∠B＝150°，∠D＝130°，则∠C的度数是.

查看试题解析
17. 如图，将三角形ABC沿BC方向平移3cm得到三角形DEF，若三角形ABC的周长为16cm，则四边形ABFD的周长为 cm．

查看试题解析
18. 小明在计算一道整式乘法的题： $(x - m) (3 x + 5)$ ，因为把“-m”抄成了“+m”，得到的结果是 $3 x^{2} + 11 x + 10$ ，则m的值为．

查看试题解析
19. 若 $a + b + c = 0$ ， $a^{3} + b^{3} + c^{3} = 0$ ，则 $a^{23} + b^{23} + c^{23} =$ ．

查看试题解析
20. 阅读材料后解决问题：
小明遇到下面一个问题：计算(2+1)(2²+1)(2⁴+1)(2⁸+1)。

经过观察，小明发现如果将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：

(2+1)(2²+1)(2⁴+1)(2⁸+1)=(2-1)(2+1)(2²+1)(2⁴+1)(2⁸+1)=(2²-1)(2²+1)(2⁴+1)(2⁸+1)=(2⁴-1)(2⁴+1)(2⁸+1)=(2⁸-1)(2⁸+1)=2¹⁶-1

请你仿照小明解决问题的方法，尝试计算：(6+1)(6²+1)(6⁴+1)(6⁸+1)=。

查看试题解析

三、计算题（共12分）

21. 计算

(1)、 $3^{- 2} \div 3^{4}$ ；

(2)、 $2020^{0} - 2^{2} + {(\frac{1}{3})}^{- 1}$ ；

(3)、 ${\begin{array}{l} 2 x + 3 y = 5 \\ x - y = 1 \end{array}$

(4)、 ${\begin{array}{l} 2 x + 5 y = 3 \\ 5 x - 3 y = 6 \end{array}$

查看试题解析

四、作图题（共10分）

22. 在如图所示的方格纸中，每个小正方形的边长都是1个单位长度，每个小正方形的顶点叫格点，三角形ABC的三个頂点都在格点上.

(1)、①画出三角形ABC向上平移4个单位后的三角形A₁B₁C₁（点A，B，C的对应点为点A₁ ， B₁ ， C₁）；
②画出三角形A₁B₁C₁向左平移5个单位后的三角形A₂B₂C₂（点A₁ ， B₁ ， C₁的对应点为点A₂ ， B₂ ， C₂）；

(2)、分别连接AA₁ ， A₁A₂ ， AA₂ ，并直接写出三角形AA₁A₂的面积为平方单位.

查看试题解析

五、解答题（共4题，共38分）

23. 已知 $m^{2} - 2 m n - 1 = 0$ ，求代数式 ${(m - n)}^{2} + (m + n) (m - n) - m^{2}$ 的值．

查看试题解析
24. 今年疫情期间某物流公司计划用两种车型运输救灾物资，用2辆A型车和1辆B型车装满物资一次可运10吨；用1辆A型车和2辆B型车一次可运11吨．某物流公司现有31吨货物资，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都装满．

(1)、1辆A型车和1辆B型车都装满物资一次可分别运多少吨？

(2)、请你帮该物流公司设计租车方案，并把符合要求的租车方案都列出来；

(3)、若A型车每辆需租金每次100元，B型车每辆租金每次120元，请从（2）中的方案里选出最省钱的租车方案，并求出最少租车费．

查看试题解析
25. 如图，将两个长方形用不同方式拼成图1和图2两个图形．

(1)、若图1中的阴影部分面积为 $a^{2} - b^{2}$ ，则图2中的阴影部分面积为（用含字母a，b的代数式表示）；

(2)、由（1）你可以得到的等式是；

(3)、根据你所得到的等式解决下面的问题：
①若 $x^{2} - y^{2} = 16$ ， $x - y = 2$ ，则 $x + y =$ ；

②计算： $67.7 5^{2} - 32.2 5^{2}$ ．

查看试题解析
26. 如图1，直线 $M N$ 与直线 $A B$ 、 $C D$ 分别交于点E、F， $∠ 1 + ∠ 2 = 180 °$ ．

(1)、请直接写出直线 $A B$ 与 $C D$ 的位置关系；

(2)、如图2，动点P在直线 $A B$ ， $C D$ 之间，且在直线 $M N$ 左侧，连接 $E P$ ， $F P$ ，探究 $∠ A E P$ ， $∠ E P F$ ， $∠ P F C$ 之间的数量关系．

小明经过分析证明的过程如下：过点P作 $P H$ // $A B$ ． ∴ $∠ A E P =$ （两直线平行，内错角相等）．

∵ $A B$ // $C D$ （已知），

∴ $C D$ // $P H$ （平行于同一条直线的两条直线平行）．

∴ $∠ P F C = ∠ H P F$ （两直线平行，内错角相等）．

∵ $∠ E P F = ∠ E P H + ∠ H P F$ ，

∴（等量代换）．

请你补全上述的证明过程．

(3)、小明进一步探究，分别作出 $∠ P E B$ 和 $∠ P F D$ 的角平分线，若两条角平分线交于点 $Q$ ，如图3．

①若 $∠ E P F = 90 °$ ，则 $∠ E Q F$ ．

②探究 $∠ E P F$ 与 $∠ E Q F$ 的数量关系，小明思路如下：设 $∠ E P F = α$ ，进一步可知 $∠ P E B + ∠ P F D =$ （用含 $α$ 的式子表示）．设 $∠ E Q F = β$ ．用等式表示 $α$ 与 $β$ 的数量关系．

查看试题解析