2023年浙教版七年级下学期数学期中模拟卷（3）

试卷更新日期：2023-04-01 类型：期中考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 北京 2022年冬奥会会徽是以汉字“冬”为灵感来源设计的.在下面的四个图中，由下图经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 每到四月，许多地方杨絮、柳絮如雪花漫天飞舞，人们不堪其扰，据测定，杨絮纤维的直径约为 $0.0000106$ m，该数值用科学记数法表示为（）

A、 $0.106 \times 1 0^{- 4}$ B、 $1.06 \times 1 0^{- 5}$ C、 $10.6 \times 1 0^{- 6}$ D、 $106 \times 1 0^{- 7}$

查看试题解析
3. 下列各组数中，是二元一次方程 $3 x - 5 y = 8$ 的解的是（）

A、 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = - 1 \\ y = 1 \end{array}$ C、 ${\begin{array}{l} x = - 1 \\ y = - 1 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$

查看试题解析
4. 下列运算中，正确的是（）

A、 $2 a^{2} - a^{2} = 1$ B、 ${(2 a)}^{2} = 2 a^{2}$ C、 $a^{6} \div a^{3} = a^{3}$ D、 $a^{4} \cdot a^{2} = a^{8}$

查看试题解析
5. 如图，不能推出 $a ∥ b$ 的条件是（）

A、 $∠ 1 = ∠ 3$ B、 $∠ 2 + ∠ 3 = 180 °$ C、 $∠ 2 = ∠ 4$ D、 $∠ 1 = ∠ 4$

查看试题解析
6. 若方程组 ${\begin{array}{l} 3 x + y = 1 + 3 a \\ x + 3 y = 1 - a \end{array}$ 的解满足x＋y＝0，则a的值为（）

A、－1 B、1 C、0 D、无法确定

查看试题解析
7. 如图，含30°角的直角三角尺DEF放置在△ABC上，30°角的顶点D在边AB上，DE⊥AB．若∠B为锐角，BC∥DF，则∠B的大小为（）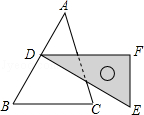

A、30° B、45° C、60° D、75°

查看试题解析
8. 下列不能用平方差公式计算的是（　　）

A、 $(x + y) (x - y)$ B、 $(- x + y) (x - y)$ C、 $(- x + y) (- x - y)$ D、 $(- x + y) (x + y)$

查看试题解析
9. 盲盒近来火爆，这种不确定的“盲抽”模式受到了大家的喜爱，一服装厂用某种布料生产玩偶A与玩偶B组合成一批盲盒，一个盲盒搭配1个玩偶A和2个玩偶B，已知每米布料可做1个玩偶A或3个玩偶B，现计划用136米这种布料生产这批盲盒（不考虑布料的损耗），设用x米布料做玩偶A，用y米布料做玩偶B，使得恰好配套，则下列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 136 \\ x = 3 y \end{array}$ B、 ${\begin{array}{l} x + y = 136 \\ x = 2 \times 3 y \end{array}$ C、 ${\begin{array}{l} x + y = 136 \\ 3 x = y \end{array}$ D、 ${\begin{array}{l} x + y = 136 \\ 2 x = 3 y \end{array}$

查看试题解析
10. 如图，七个相同的小长方形组成一个大长方形 $A B C D$ ，若 $C D = 21$ ，则长方形 $A B C D$ 的周长为（）

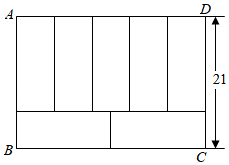A、100 B、102 C、104 D、106

查看试题解析

二、填空题（每空3分，共27分）

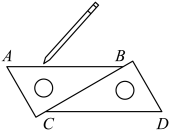
11. 计算： $- 5 x^{2} \cdot 2 x y$ 的结果等于．

查看试题解析
12. 如图，小明在两块按如图所示的方式摆放的含30°角的直角三角板的边缘画直线AB、CD，得到 $A B ∥ C D$ ，这是根据，两直线平行．

查看试题解析
13. 如图， $∠ A B D = ∠ E F D$ ， $∠ F E C$ 与 $∠ E C D$ 互补，当 $∠ F E C = 150 °$ ， $∠ A B C = 46 °$ 时， $∠ B C E$ 的度数为．

查看试题解析
14. 已知： $a^{m}$ =3， $a^{n}$ = $\frac{1}{2}$ ，则 $a^{3 m + 2 n}$ = ．

查看试题解析
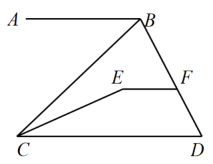15. 如图，现有正方形卡片A类，B类和长方形卡片C类若干张，如果要拼一个长为（a+4b），宽为（a+b）的大长方形，则需要C类卡片张．

查看试题解析
16. 某人用24000元买进甲、乙两种股票，在甲股票升值15%，乙股票下跌10%时卖出，共获利1350元，则此人买甲股票的钱比买乙股票的钱多元.

查看试题解析
17. 一副三角板按图1的形式摆放，把含45°角的三角板固定，含30°角的三角板绕直角顶点逆时针旋转，设旋转的角度为 $α$ （ $0 ° < α < 180 °$ ）.在旋转过程中，当两块三角板有两边平行时， $α$ 的度数为.

查看试题解析
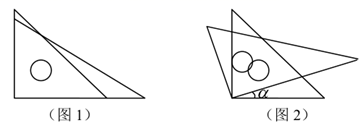18. 甲、乙二人分别从相距20km的A，B两地出发，相向而行．下图是小华绘制的甲、乙二人运动两次的情形，设甲的速度是x km/h，乙的速度是y km/h，根据题意所列的方程组是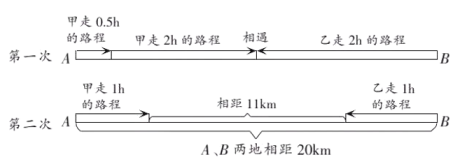， $1.5 x + y =$ ．

查看试题解析

三、解答题（共4题，共43分）

19. 已知： $a - b = 2 ， b - c = 3$ ，求 $a^{2} + b^{2} + c^{2} - a b - a c - b c$

查看试题解析
20. 如图， $∠ 1 = ∠ B C E$ ， $∠ 2 + ∠ 3 = 180 °$ ．

(1)、判断 $A C$ 与 $E F$ 的位置关系，并说明理由；

(2)、若 $C A$ 平分 $∠ B C E$ ， $E F ⊥ A B$ 于 $F$ ， $∠ 1 = 72 °$ ，求 $∠ B A D$ 的度数．

查看试题解析
21. “当好东道主，文明迎亚运”，本区对亚运场馆附近的主干道进行了改造，因道路建设需要开挖土石方，计划每小时挖掘土石方1760m³ ，现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作，租赁公司提供的挖掘机有关信息如表：

租金（单位：元/台•时）
挖掘土石方量（单位：m³/台•时）
甲型
190
160
乙型
260
240

(1)、若租用甲、乙两种型号的挖掘机共8台，恰好完成每小时的挖掘量，则甲、乙两种型号的挖掘机各需多少台？

(2)、如果每小时支付的租金不超过2000元，又恰好完成每小时的挖掘量，那么共有几种不同的租用方案？

查看试题解析
22. 在数学中，有许多关系都是在不经意间被发现的，当然，没有敏锐的观察力是做不到的，数学家们往往是这样来研究问题的：特值探究——猜想归纳——逻辑证明——总结应用，下面我们也来像数学家们那样分四步找出这两个代数式的关系：对于代数式 $(a + b) (a - b)$ 与 $a^{2} - b^{2}$ .

(1)、特值探究：当 $a = - 5 ， b = 3$ 时， $(a + b) (a - b) =$ ； $a^{2} - b^{2} =$ ；

(2)、猜想归纳：观察（1）的结果，写出 $(a + b) (a - b)$ 与 $a^{2} - b^{2}$ 的关系：.

(3)、逻辑证明：如图，边长为 $a$ 的正方形纸片剪出一个边长为 $b$ 的小正方形之后，剩余部分（即阴影部分）又剪拼成一个矩形（不重叠无缝隙），则图①中阴影面积可表示为，图②中阴影部分面积可表示为，由阴影部分的面积相等得到等式；

(4)、总结应用：利用你发现的关系，求：
①若 $a^{2} - b^{2} = 6$ ，且 $a + b = 2$ ，则 $a - b =$ ；

②计算： $10 2^{2} - 9 8^{2}$ .

查看试题解析

四、计算题（共2题，共20分）

23. 计算：

(1)、（-1）²⁰²²+（3.14-π）⁰

(2)、（-y³）⁵÷（y²）³

查看试题解析
24. 解方程组：

(1)、 ${\begin{array}{l} 2 x + y = 5 \\ 3 x - 2 y = 11 \end{array}$ ；

(2)、 ${\begin{array}{l} 4 (x + 2) + 5 y = 1 \\ 2 x + 3 (y + 2) = 3 \end{array}$ .

查看试题解析

	租金（单位：元/台•时）	挖掘土石方量（单位：m³/台•时）
甲型	190	160
乙型	260	240