2023年浙教版七年级下学期数学期中模拟卷（2）

试卷更新日期：2023-04-01 类型：期中考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 图中的同位角是（）

A、∠1和∠2 B、∠1和∠3 C、∠1和∠4 D、∠2和∠3

查看试题解析
2. 新型冠状病毒体积很小，这种病毒外直径大概在0.00000 011米，则0.00000011这个数字可用科学记数法表示为（　　）

A、 $1.1 \times 1 0^{- 6}$ B、 $1.1 \times 1 0^{- 7}$ C、 $1.1 \times 1 0^{- 8}$ D、 $0.11 \times 1 0^{- 8}$

查看试题解析
3. 下列各式中，正确的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 $a^{3} \cdot a^{3} = a^{9}$ C、 ${(a b)}^{2} = a^{2} b^{2}$ D、 ${(a^{2})}^{3} = a^{5}$

查看试题解析
4. 若 $(a - 2) x^{| a - 1 |} - 3 y = 5$ 是关于 $x$ 、 $y$ 的二元一次方程，则 $a$ 的值为（）

A、0 B、2 C、0或2 D、1或2

查看试题解析
5. 关于x，y的二元一次方程组 ${\begin{array}{l} 2 x + y = m - 1 \\ x - y = 1 \end{array}$ 的解是 ${\begin{array}{l} x = 3 \\ y = ■ \end{array}$ ．其中y的值被遮盖了，则m，y的值为（）

A、 $m = 9 ， y = 2$ B、 $m = 7 ， y = 2$ C、 $m = 11 ， y = 4$ D、 $m = 9 ， y = 4$

查看试题解析
6. 下列多项式乘法中，能运用平方差公式进行计算的是（）

A、 $(2 x + y) (- 2 x - y)$ B、 $- (2 x + y) (- 2 x - y)$ C、 $(- 2 x - y) (- 2 x + y)$ D、 $(- 2 x + y) (y - 2 x)$

查看试题解析
7. 如图，点E在 $A C$ 的延长线上，下列条件不能判定 $A B ∥ C D$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 = ∠ 4$ C、 $∠ A = ∠ D C E$ D、 $∠ A + ∠ 2 + ∠ 4 = 180 °$

查看试题解析
8. 若 $(x - 2021) (x - 2022) = 6$ ，则 ${(2021 - x)}^{2} + {(2022 - x)}^{2}$ 的值是（）

A、11 B、12 C、13 D、14

查看试题解析
9. 如图，将一副三角板的直角顶点重合，且使 $A B ∥ C D$ ，则 $∠ D E B$ 的度数是（）

A、 $1 5^{∘}$ B、 $2 0^{∘}$ C、 $6 5^{∘}$ D、 $9 5^{∘}$

查看试题解析
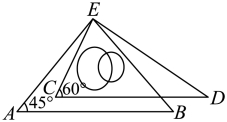10. 我国古代数学巨著《孙子算经》中的“鸡兔同笼”题为：“今有雉（鸡）兔同笼，上有三十五头，下有九十四足．问雉兔各几何”，正确答案是（）

A、鸡24只，兔11只 B、鸡23只，兔12只 C、鸡11只，兔24只 D、鸡12只，兔23只

查看试题解析

二、填空题（每空4分，共24分）

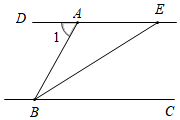
11. 写出一个解为 ${\begin{cases} x = 1 \\ y = 2 \end{cases}$ 的二元一次方程．

查看试题解析
12. 如图，已知DE $∥$ BC，BE平分∠ABC，若∠1=70°，则∠AEB的度数为.

查看试题解析
13. 在长为10m，宽为8m的矩形空地上，沿平行于矩形各边的方向分割出三个长相等，宽相等的小矩形花圃，其示意图如图所示．则花圃的面积为．

查看试题解析
14. 如图，△ABC的周长是20cm，现将△ABC沿AB方向平移2cm至△A'B'C'的位置，连接CC'，则四边形AB'C'C的周长是 cm．

查看试题解析
15. 已知 $1 0^{m} = 3 ， 1 0^{n} = 2$ ，则 $1 0^{2 m + n} =$ ．

查看试题解析
16. 从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出，已知入射光线OA的反射光线为AB， $∠ O A B = ∠ C O A = 72 °$ ．在如图中所示的截面内，若入射光线OD经反光罩反射后沿DE射出，且 $∠ O D E = 27 °$ ，则 $∠ A O D$ 的度数是．

查看试题解析

三、计算题（共2题，共12分）

17. 计算：

(1)、 $| - 3 | + (- 1)^{2021} \times (π - 3.14)^{0} - {(- \frac{1}{2})}^{- 2}$ ．

(2)、 $202 1^{2} - 2022 \times 2020$ （用简便方法计算）．

查看试题解析
18. 解方程组：

(1)、 ${\begin{array}{l} y = 2 x - 4 ① \\ 3 x + y = 1 ② \end{array}$

(2)、 ${\begin{array}{l} x + \frac{2 y + 1}{2} = 4 (x - 1) \\ 3 x - 2 (2 y + 1) = 4 \end{array}$

查看试题解析

四、作图题（共8分）

19. 如图，在10×10的正方形网格中，每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上，且通过两次平移（沿网格线方向作上下或左右平移）后得到△ $A' B' C'$ ，点C的对应点是直线上的格点 $C'$ .

(1)、画出△ $A' B' C'$ .

(2)、若连接 $A A'$ 、 $B B'$ ，则这两条线段之间的关系是.

(3)、试在直线 $l$ 上画出所有符合题意的格点P，使得由点 $A'$ 、 $B'$ 、 $C'$ 、P四点围成的四边形的面积为9.

查看试题解析

五、解答题（共5题，共46分）

20. 先化简，再求值： $[(x + y) (x - y) - (x - y)^{2}] \div 2 y$ ，其中 $x = 2022$ ， $y = 1$ ．

查看试题解析
21. 乘法公式的探究及应用．

(1)、如图，若将阴影部分裁剪下来，重新拼成一个长方形，面积是（写成多项式乘法的形式）

(2)、比较左、右两图的阴影部分面积，可以得到乘法公式（用式子表达）．

(3)、运用你所得到的公式，计算下列各题：
① $10.3 \times 9.7$
② $(2 m + n - p) (2 m - n + p)$

查看试题解析
22. 已知，直线 $A B / / D C$ ，点P为平面内一点，连接 $A P$ 与 $C P$ .

(1)、如图1，点P在直线 $A B$ 、 $C D$ 之间，若 $∠ B A P = 50 °$ ， $∠ D C P = 20 °$ ，求 $∠ A P C$ 的度数.

(2)、如图2，点P在直线 $A B$ 、 $C D$ 之间， $∠ B A P$ 与 $∠ D C P$ 的角平分线相交于点K，写出 $∠ A K C$ 与 $∠ A P C$ 之间的数量关系，并说明理由.

(3)、如图3，点P在直线 $A B$ 、 $C D$ 下方， $∠ B A P$ 与 $∠ D C P$ 的角平分线相交于点K，直接写出 $∠ A K C$ 与 $∠ A P C$ 之间的数量关系.

查看试题解析
23. 某工厂加工圆柱形的茶叶盒，购买了n块相同的金属板材，已知每块金属板材可以有A，B，C三种裁剪方式，如图，A方式：裁剪成9个圆形底面和1个侧面.B方式：裁剪成4个侧面.C方式：裁剪成12个圆形底面.已知2个圆形底面和1个侧面组成一个圆柱形茶叶盒，且要求圆形底面与侧面恰好配套.现已有4块金属板材按C方式裁剪.

(1)、设有 $x$ 块金属板材按A方式裁剪，y块金属板材按B方式裁剪.
①可以裁剪出圆形底面共个（用含x的代数式表示），侧面共个（用含x，y的代数式表示）；

②当 $n = 25$ 时，最多能加工多少个圆柱形茶叶盒？

(2)、现将n块相同的金属板材全部裁剪完，为了使加工成的圆形底面与侧面恰好配套，则n的值可以是.（其中 $50 ≤ n ≤ 70$ ）

查看试题解析
24. 若x满足(9 $-$ x)(x $-$ 4)=4，求(9 $-$ x)² $+$ (x $-$ 4)²的值.
解：设9 $-$ x=a，x $-$ 4=b，则(9 $-$ x)(x $-$ 4)=ab=4，a $+$ b=(9 $-$ x) $+$ (x $-$ 4)=5
∴(9 $-$ x)² $+$ (x $-$ 4)²=a²+b²=(a+b)² $-$ 2ab=5²—2 $\times$ 4=17

请仿照上面的方法求解下面问题：

(1)、若x满足 $(x - 10) (x - 20) = 15$ ，求 ${(x - 10)}^{2} + {(x - 20)}^{2}$ 的值；

(2)、若x满足 ${(x - 2021)}^{2} + {(x - 2022)}^{2} = 33$ ，求 $(x - 2021) (x - 2022)$ 的值

(3)、已知正方形ABCD的边长为x，E，F分别是AD、DC上的点，且AE=1，CF=3，长方形 EMFD的面积是48，分别以MF，DF为边长作正方形MFRN和正方形GFDH，求阴影部分的面积.

查看试题解析