2023年浙教版七年级下学期数学期中模拟卷（1）

试卷更新日期：2023-04-01 类型：期中考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图， $△ A B C$ 沿射线 $B C$ 方向平移到 $△ D E F$ （点E在线段 $B C$ 上），如果 $B C = 7 c m$ ， $E C = 4 c m$ ，那么平移距离为（）

A、 $3 c m$ B、 $5 c m$ C、 $8 c m$ D、 $13 c m$

查看试题解析
2. 如图，l₁∥l₂ ，将一副直角三角板作如下摆放，图中点A、B、C在同一直线上，则∠1的度数为（）

A、100° B、120° C、75° D、150°

查看试题解析
3. 若关于 $x$ 、 $y$ 的方程组 ${\begin{array}{l} x + 2 y = 3 a - 1 \\ 2 x + y = 7 \end{array}$ 的解满足 $x + y = 3$ ，则 $a$ 的值是（）

A、4 B、 $- 1$ C、2 D、1

查看试题解析
4. 若 $(x - 3) (x^{2} + a x + b)$ 的积中不含x的二次项和一次项，则a和b的值（）

A、a＝0；b＝2 B、a＝3；b＝9 C、a＝－1；b＝2 D、a＝2；b＝4

查看试题解析
5. 在一次数学活动课上，老师让同学们用两个大小、形状都相同的三角板画平行线 $A B$ ， $C D$ ，贝贝、晶晶、欢欢三位同学的做法如图所示：

上述三位同学的做法中，依据“内错角相等，两直线平行”的是（）

A、仅贝贝同学 B、贝贝和晶晶 C、晶晶和欢欢 D、贝贝和欢欢

查看试题解析
6. 已知方程组 ${\begin{cases} 5 x + y = 3 \\ a x + 5 y = 4 \end{cases}$ 与 ${\begin{cases} 5 x + b y = 1 \\ x - 2 y = 5 \end{cases}$ 有相同的解，则a，b的值为（）

A、 ${\begin{cases} a = 1 \\ b = 2 \end{cases}$ B、 ${\begin{cases} a = - 4 \\ b = - 6 \end{cases}$ C、 ${\begin{cases} a = - 6 \\ b = 2 \end{cases}$ D、 ${\begin{cases} a = 14 \\ b = 2 \end{cases}$

查看试题解析
7. 已知关于x，y的方程组 ${\begin{array}{l} x + 2 y = 5 - a \\ x - y = 2 a - 1 \end{array}$ ，给出下列结论：
①当 $a = 0$ 时，方程组的解也是 $2 x + y = 3$ 的解．②无论a取何值，x，y的值不可能是互为相反数；③x，y都为自然数的解有4对：其中正确的个数是（）

A、3个 B、2个 C、1个 D、0个

查看试题解析
8. 已知 $x + \frac{1}{x} = 8$ ，则 $x^{2} + \frac{1}{x^{2}}$ 的值是（）

A、 $66$ B、 $64$ C、62 D、60

查看试题解析
9. 式子 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) ⋯ ⋯ (2^{1010} + 1) + 1$ 化简的结果为（）

A、 $2^{1010}$ B、 $2^{1010} + 1$ C、 $2^{2020}$ D、 $2^{2020} + 1$

查看试题解析
10. 某H品牌手机上使用5nm芯片，1nm＝0.0000001cm，则5nm用科学记数法表示为（）

A、 $50 \times 10^{- 8} c m$ B、 $0.5 \times 10^{- 7} c m$ C、 $5 \times 10^{- 7} c m$ D、 $5 \times 10^{- 8} c m$

查看试题解析

二、填空题（每空4分，共24分）

11. 如果 ${(x + y + 2)}^{2} + | x - y - 6 | = 0$ ，那么 $x y =$ ．

查看试题解析
12. 如图，已知AB∥EG，BC∥DE，CD∥EF，则x、y、z三者之间的关系是．

查看试题解析
13. 如图， $A B = 3 c m$ ， $B C = 4 c m$ ， $A C = 2 c m$ ，将 $△ A B C$ 沿BC方向平移 $2.5 c m$ ，得到 $△ D E F$ ，连接AD，则阴影部分的周长为cm．

查看试题解析
14. 若关于x、y的方程组 ${\begin{array}{l} a x + b y = c \\ m x + n y = d \end{array}$ 的解为 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ ，则方程组 ${\begin{array}{l} a (x - 1) - 3 b y = 3 c \\ m (x - 1) - 3 n y = 3 d \end{array}$ 的解是.

查看试题解析
15. 已知二次三项式x²+px+q因式分解的结果是（x﹣3）（x﹣5），则（2p+q）²⁰²⁰ ．

查看试题解析
16. 一副直角三角尺叠放如图1所示，现将 $45 °$ 的三角尺 $A D E$ 固定不动，将含 $30 °$ 的三角尺 $A B C$ 绕顶点A顺时针转动，使两块三角尺至少有一组边互相平行．如图2：当 $∠ C A E = 60 °$ 时， $B C / / D E$ ．则 $∠ C A E (0 ° < ∠ C A E < 180 °)$ 其它所有可能符合条件的度数为．

查看试题解析

三、计算题（共2题，共14分）

17. 解方程组：

(1)、 ${\begin{array}{l} 3 x + 2 y = 1 \\ 3 x - 2 y = 9 \end{array}$

(2)、 ${\begin{array}{l} 3 (x + y) = x - y \\ \frac{x + y}{2} + \frac{x - y}{6} = 1 \end{array}$

查看试题解析
18. 解方程组 ${\begin{cases} 2 x + y + z = - 7 ① \\ x + 2 y + z = - 8 ② \\ x + y + 2 z = - 9 ③ \end{cases}$

查看试题解析

四、解答题（共5题，共52分）

19. 已知 $a^{m} = 2$ ， $a^{n} = 5$ ，求下列各式的值.

(1)、 $a^{m + n}$

(2)、 $a^{3 m + 2 n}$

查看试题解析
20. 如图. $A D ∥ B C ， ∠ 1 = ∠ B ， ∠ 2 = ∠ 3$ .

注：本题第（1）、（2）小题在下面的解答过程的空格内填写理由或数学式；第（3）小题要写出解题过程.

(1)、试说明： $E B ∥ D C$ ；
∵ $A D ∥ B C$ ，（已知）

∴ $∠ B = ∠$       ▲      （             ）

又∵ $∠ 1 = ∠ B$ ，（已知）

∴ $∠ 1 = ∠$       ▲      （等量代换）

∴      ▲       $∥$       ▲      （             ）

(2)、 $A C$ 与 $E D$ 的位置关系如何?为什么?
$A C$ 与 $E D$ 的位置关系是：                ，理由如下：
∵ $A D ∥ B C$ ，（已知）

∴ $∠ 3 = ∠$       ▲      （              ）

又∵ $∠ 2 = ∠ 3$ ，（已知）

∴∠      ▲      =∠      ▲      （等量代换）

∴      ▲      //      ▲      .（               ）

(3)、 $∠ B E D$ 与 $∠ A C D$ 相等吗?请说明理由.

查看试题解析

21. 在疫情防控期间，某中学为保障广大师生生命健康安全，欲从商场购进一批免洗手消毒液和84消毒液.已知如下购买情况：

	免洗手消毒液	84消毒液	总花费
第一次购买	40瓶	90瓶	1320
第二次购买	60瓶	120瓶	1860

(1)、求每瓶免洗手消毒液和每瓶84消毒液的价格分别是多少元？

(2)、若商场有两种促销方案：

方案一：所有购买商品均打九折；

方案二：每购买5瓶免洗手消毒液送2瓶84消毒液；

学校打算购进免洗手消毒液100瓶，84消毒液60瓶，请问学校选用哪种方案更省钱？省多少钱？

查看试题解析

22.

(1)、从图1-3中任意选择一个，通过计算图中阴影部分的面积，可得到关于a、b的等量关系是；

(2)、尝试解决：
①已知： $m + n = 2$ ， $m^{2} + n^{2} = 7$ ，则 $m n$ = ▲ ；

②已知： $2 a + b = 3$ ， $a b = 1$ ，求 $(2 a - b)^{2}$ 的值；

③已知： $(4 - x) (5 - x) = 6$ ，求 $(4 - x)^{2} + (5 - x)^{2}$ 的值；

(3)、填数游戏：如图4，把数字1~9填入构成三角形形状的9个圆圈中，使得各边上的四个数字的和都等于21，将每边四个数字的平方和分别记 $A$ 、 $B$ 、 $C$ ，已知 $A + B + C = 411$ .如果将位于这个三角形顶点处的三个圆圈填入的数字分别表示为x、y、x+y，求xy的值 .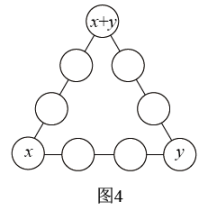

查看试题解析
23.

(1)、问题情境：如图1， $A B ∥ C D$ ， $∠ P M B = 140 °$ ， $∠ P N D = 120 °$ ，求 $∠ M P N$ 的度数；

(2)、问题迁移：在（1）的条件下，如图2， $∠ A M P$ 的角平分线与 $∠ C N P$ 的角平分线交于点F，则 $∠ M F N$ 的度数为多少？请说明理由；

(3)、问题拓展：如图3， $A B ∥ C D$ ，点P在射线 $O M$ 上移动时（点P与点O，M，D三点不重合），记 $∠ P A B = α$ ， $∠ P C D = β$ ，请直接写出 $∠ A P C$ 与 $α$ ， $β$ 之间的数量关系．

查看试题解析