2023年浙教版数学七年级下学期高分速效复习7 因式分解（基础版）

试卷更新日期：2023-04-01 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列式子从左到右变形是因式分解的是（）

A、 $10 x y^{2} = 2 x \cdot 5 y^{2}$ B、 $(x + y) (x - y) = x^{2} - y^{2}$ C、 $x^{2} - 3 x + 1 = x (x - 3) + 1$ D、 $x^{2} + x - 6 = (x + 3) (x - 2)$

查看试题解析
2. 把多项式 $a^{2} - 9 a$ 分解因式，结果正确的是（）

A、 $a (a - 9)$ B、 $(a + 3) (a - 3)$ C、 $a (a + 3) (a - 3)$ D、 $- a (a - 9)$

查看试题解析
3. 下列添括号正确的是（）

A、 $b + c = - (b + c)$ B、 $- 2 x + 4 y = - 2 (x - 4 y)$ C、 $a - b = + (a - b)$ D、 $2 x - y - 1 = 2 x - (y - 1)$

查看试题解析
4. 多项式 $8 a^{3} b^{2} + 12 a^{3} b c - 4 a^{2} b$ 中，各项的公因式是（）

A、 $a^{2} b$ B、 $- 4 a^{2} b^{2}$ C、 $4 a^{2} b$ D、 $- a^{2} b$

查看试题解析
5. 下列各式从左到右变形是因式分解，并分解正确的是（）

A、 $(a - b)^{2} + (a - b) = (a - b) (a - b + 1)$ B、 $(x + 2) (x + 3) = x^{2} + 5 x + 6$ C、 $4 a^{2} - b^{2} = (4 a - b) (4 a + b)$ D、 $m^{2} - n^{2} + 2 m n = {(m - n)}^{2}$

查看试题解析
6. 如图，边长为 $a$ 、 $b$ 的长方形周长为 $10$ ，面积为 $8$ ，则 $a^{2} b + a b^{2}$ 的值为（）

A、 $40$ B、 $60$ C、 $80$ D、 $100$

查看试题解析
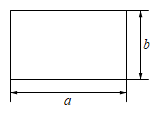7. 下列能用平方差公式进行因式分解的是（）

A、 $x^{2} + 1$ B、 $x^{2} - 1$ C、 $- x^{2} - y^{2}$ D、 $x^{2} + 4 x + 4$

查看试题解析
8. 下列等式中，从左到右的变形属于因式分解且分解彻底的是（）

A、 $a^{3} + 2 a^{2} + a = a {(a + 1)}^{2}$ B、 $a (a - b) = a^{2} - a b$ C、 $x^{4} - 1 = (x^{2} + 1) (x^{2} - 1)$ D、 $a x^{2} - a b x + a = a (x^{2} - b x) + a$

查看试题解析
9. 课堂上老师在黑板上布置了如框所示的题目，小聪马上发现了其中有一道题目错了，你知道是哪道题目吗?（）

用平方差公式分解下列各式：

（1） $a^{2} - b^{2}$

（2） $49 x^{2} - y^{2} z^{2}$

（3） $- x^{2} - y^{2}$

（4） $16 m^{2} n^{2} - 25 p^{2}$

A、第1道题 B、第2道题 C、第3道题 D、第4道题

查看试题解析
10. 将多项式 $16 m^{2} + 1$ 加上一个单项式后，使它能够在我们所学范围内因式分解，则此单项式不能是（）

A、-2 B、 $- 15 m^{2}$ C、8m D、 $- 8 m$

查看试题解析

二、填空题（每空3分，共21分）

11. 叫做因式分解．

查看试题解析
12. 若x²﹣ax﹣1可以分解为（x﹣2）（x+b），则a= ， b=

查看试题解析
13. 在括号内填入适当的项： $a - b + c = a -$ ．

查看试题解析
14. 多项式 $5 x^{2} - 3 x$ 的公因式是.

查看试题解析
15. 因式分解：2x(a-b)-6y(b-a)=.

查看试题解析
16. 如果 $x^{2} + 2 (m - 3) x + 4$ 是完全平方式，则 $m$ 的值是.

查看试题解析

三、计算题（共2题，共24分）

17. 因式分解：

(1)、 $a b^{2} + b^{3}$

(2)、 $16 x^{2} - 8 x y + y^{2}$

(3)、 ${(m^{2} - 3)}^{2} - 4 m^{2}$

(4)、 $x^{2} - 2 x + 2 x y + y^{2} - 2 y + 1$

查看试题解析
18. 分解因式

(1)、 $(a - 4) b + (4 - a) c$

(2)、 $10 a {(x - y)}^{2} - 5 b (y - x)$

(3)、 $x (x + y) (x - y) - x {(x + y)}^{2}$

(4)、 $9 x^{2} - y^{2} + 6 x + 1$

查看试题解析

四、解答题（共6题，共45分）

19. 在① $4 m n$ ② $- 4 m n$ 这两个代数式中选择其中一个，补充在下面问题横线上，并完成问题的解答：
问题：分解因式： $m^{2} +$ ▲ $+ 4 n^{2}$

查看试题解析
20. 如果 $Δ A B C$ 的三边长 $a ， b ， c$ 满足等式 $a^{2} + b^{2} + c^{2} - a b - b c - c a = 0$ ，试判断此 $Δ A B C$ 的形状并写出你的判断依据．

查看试题解析
21. 在日常生活中，如取款、上网需要密码，有一种因式分解法产生密码，例如 $x^{4} - y^{4} = (x - y) (x + y) (x^{2} + y^{2})$ ，当 $x = 9 ， y = 9$ 时， $x - y = 0$ ， $x + y = 18$ ， $x^{2} + y^{2} = 162$ ，则密码018162或180162等.对于多项式 $4 x^{3} - x y^{2}$ ，取 $x = 10 ， y = 10$ ，用上述方法产生密码是什么？

查看试题解析
22. 下面是某同学对多项式 $(x^{2} - 4 x + 2) (x^{2} - 4 x + 6) + 4$ 进行分解因式的过程.
解：设 $x^{2} - 4 x = y$ ，

原式 $= (y + 2) (y + 6) + 4$ (第一步)

$= y^{2} + 8 y + 16$ (第二步)

$= {(y + 4)}^{2}$ (第三步)

$= {(x^{2} - 4 x + 4)}^{2}$ .(第四步)

回答下列问题：

(1)、该同学第二步到第三步运用了分解因式的（）

A、提取公因式 B、逆用平方差公式 C、逆用完全平方公式

(2)、该同学分解因式的结果不正确，应更正为.

(3)、分解因式：n(n+1)(n+2)(n+3)+1.

查看试题解析
23. 阅读材料题：在因式分解中，有一类形如x²+（m+n）x+mn的多项式，其常数项是两个因数的积，而它的一次项系数恰是这两个因数的和，则我们可以把它分解成x²+（m+n）x+mn＝（x+m）（x+n）．
例如：x²+5x+6＝x²+（2+3）x+2×3＝（x+2）（x+3）．

运用上述方法分解因式：

(1)、x²+6x+8；

(2)、x²﹣x﹣6；

(3)、x²﹣5xy+6y²；

(4)、请你结合上述的方法，对多项式x³﹣2x²﹣3x进行分解因式．

查看试题解析
24. 如图1，有若干张边长为α的小正方形①，长为b、宽为α的长方形②以及边长为b的大正方形3的纸片.

(1)、已知小正方形1与大正方形3的面积之和为169，长方形②的周长为34，求长方形2的面积；

(2)、如果现有小正方形①2张，大正方形31张，长方形②3张，请你将它们拼成一个大长方形(在图2虚线框内画出图形)，并运用面积之间的关系，将多项式 $2 a^{2} + 3 a b + b^{2}$ 分解因式.

查看试题解析