2023年浙教版数学七年级下学期高分速效复习6 整式的乘除（进阶版）

试卷更新日期：2023-04-01 类型：复习试卷

进入出卷网下载

一、单选题（每题2分，共20分）

1. 已知 $3^{x} = 4 ， 3^{y} = 6 ， 3^{z} = 12$ ，则x、y、z三者之间关系正确的是（）

A、xy=2z B、x+y=2z C、x+2y=2z D、x+2y=z

查看试题解析
2. 下列计算中，错误的是（）

A、 ${(\frac{3 y}{- x^{2}})}^{3} = \frac{- 9 y^{3}}{x^{6}}$ B、 ${(\frac{4 b^{3}}{- 3 c^{2}})}^{2} = \frac{16 b^{6}}{9 c^{4}}$ C、 ${(\frac{5 x^{3} y^{2}}{- 2 z})}^{2} = \frac{25 x^{6} y^{4}}{4 z^{2}}$ D、 ${(\frac{b^{2}}{- a^{3}})}^{2} = \frac{b^{4}}{a^{6}}$

查看试题解析
3. 已知单项式6a^m+1bⁿ⁺¹与﹣4a^2m^﹣1b²ⁿ^﹣1的积与7a³b⁶是同类项，则mⁿ的值为（　　）

A、1 B、2 C、3 D、4

查看试题解析
4. 若多项式 $2 x^{2} + a x - 6$ 能分解成两个一次因式的积，且其中一个次因式 $2 x - 3$ ，则 $a$ 的值为（）

A、1 B、5 C、-1 D、-5

查看试题解析
5. 有两个正方形A，B.现将B放在A的内部得图甲，将A，B构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12，若三个正方形A和两个正方形B得图丙，则阴影部分的面积为（　　）

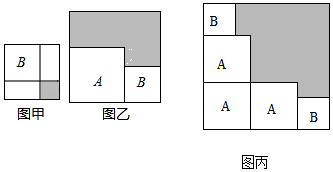A、28 B、29 C、30 D、31

查看试题解析
6. 已知 $a = 2019 x + 2019$ ， $b = 2019 x + 2020$ ， $c = 2019 x + 2021$ ，则 $a^{2} + b^{2} + c^{2} - a b - a c - b c$ 的值为 $($ ）

A、0 B、1 C、2 D、3

查看试题解析
7. 已知2ⁿ＋2¹²＋1（n＜0）是一个有理数的平方，则n的值为（）

A、﹣16 B、﹣14 C、﹣12 D、﹣10

查看试题解析
8. 原子是化学变化中的最小微粒，按照国际单位制的规定，质量单位是“kg”．例如：1个氧原子的质量是 $2.657 \times 1 0^{- 26} k g$ ．如果小数0.000…02657用科学记数法表示为 $2.657 \times 1 0^{- 26}$ ，那么这个小数中的“0”有（）

A、25个 B、26个 C、27个 D、28个

查看试题解析
9. 已知 $a \neq 0$ ，给出四个代数式，其中有一个代数式与其余代数式的化简结果不相等，则这个代数式是（）

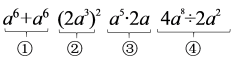A、① B、② C、③ D、④

查看试题解析
10. 我们经常利用完全平方公式以及变形公式进行代数式变形.已知关于a的代数式 $A = a^{2} + a$ ，请结合你所学知识，判断下列说法：①当 $a = - 2$ 时， $A = 2$ ；②无论a取任何实数，不等式 $A + \frac{1}{4} \geq 0$ 恒成立；③若 $A - 1 = 0$ ，则 $a^{2} + \frac{1}{a^{2}} = 3$ .正确的有（）

A、3个 B、2个 C、1个 D、0个

查看试题解析

二、填空题（每空3分，共18分）

11. 计算： ${(- \frac{2}{3})}^{2023} \cdot {(- \frac{3}{2})}^{2021} =$ .

查看试题解析
12. 已知 $6^{x} = 192$ ， $32^{y} = 192$ ，则 ${[(x - 1) (1 - y)]}^{2019} =$ .

查看试题解析
13. 某同学在计算多项式A乘 $2 x^{2}$ 时，因抄错运算符号，算成了加 $2 x^{2}$ ，得到的结果是 $x^{2} - 4 x + 1$ ，那么正确的计算结果是.

查看试题解析
14. $(1 + 2) (1 + 2^{2}) (1 + 2^{4}) (1 + 2^{8}) + 1$ 的结果是．

查看试题解析
15. 已知（2021-a）（a-2022）＝5，则（a-2021）²+（a-2022）²＝．

查看试题解析
16. 如图，现有A，C两类正方形卡片和B类长方形卡片各若干张，用它们可以拼成一些新的长方形．如果要拼成一个长为（3a+b），宽为（a+2b）的长方形，那么需要B类长方形卡片张．

查看试题解析

三、计算题（共3题，共27分）

17. 计算题

(1)、 $(3.14 - π)^{0} - | - 3 | + (- \frac{1}{2})^{- 2} - (- 1)^{2018}$ ；

(2)、2021²-4040×2021+2020²；

(3)、99×101；

(4)、（1 $- \frac{1}{2^{2}}$ ）（1 $- \frac{1}{3^{2}}$ ）（1 $- \frac{1}{4^{2}}$ ）（1 $- \frac{1}{5^{2}}$ ）…（1 $- \frac{1}{10 0^{2}}$ ）.

查看试题解析
18. 化简求值：

(1)、 $(3 x^{4} - 2 x^{3}) \div (- x) - (x - x^{2}) \cdot 3 x ，$ 其中 $x = - \frac{1}{3}$ ；

(2)、 ${(a - 3 b)}^{2} + {(3 a + b)}^{2} - {(a + 5 b)}^{2} + {(a - 5 b)}^{2} ，$ 其中 $a = - 6 ， b = - 4$ .

查看试题解析
19. 先化简，再求值.

(1)、 $(2 x + y) (2 x - y) - 4 x (x - y)$ ，其中 $x = \frac{1}{2} ， y = - 1$ ；

(2)、已知 $x^{2} - 3 x + 2 = 0$ ，求代数式 $(x - 1) (3 x + 1) - {(x + 2)}^{2} + 5$ 的值；

(3)、已知 $x^{3 m} = 2 ， y^{2 m} = 3$ ，求 ${(x^{2 m})}^{3} + {(y^{m})}^{6} - {(x^{2} y)}^{3 m} \cdot y^{m}$ 的值.

查看试题解析

四、解答题（共2题，共14分）

20. 若 $a^{m} = a^{n} (a > 0$ 且 $a \neq 1 ， m ， n$ 是正整数)，则 $m = n$ .利用上面的结论解决下面的问题.

(1)、如果 $2 \div 8^{x} \cdot 16^{x} = 2^{5}$ ，求 $x$ 的值；

(2)、如果 $2^{x + 2} + 2^{x + 1} = 24$ ，求 $x$ 的值.

查看试题解析
21. 某种产品的原料提价，因而厂家决定对产品进行提价，现有三种方案：
①第一次提价p%，第二次提价q%；

②第一次提价q%，第二次提价p%；

③第一、二次提价均为 $\frac{p + q}{2} %$ .

其中p，q是不相等的正数，三种方案哪种提价最多？

查看试题解析

五、解答题（共5题，共41分）

22. 我们将 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ 进行变形，如： $a^{2} + b^{2} = {(a + b)}^{2} - 2 a b$ ， $a b = \frac{{(a + b)}^{2} - (a^{2} + b^{2})}{2}$ 等.根据以上变形解决下列问题：

(1)、已知 $a^{2} + b^{2} = 12$ ， ${(a + b)}^{2} = 20$ ，则 $a b =$ ；

(2)、若x满足 ${(2022 - x)}^{2} + {(x - 2019)}^{2} = 2020$ ，求 $(2022 - x) (x - 2019)$ 的值；

(3)、如图，在长方形 $A B C D$ 中， $A B = 10$ ， $B C = 6$ ，点E、F分别是 $B C$ 、 $C D$ 上的点，且 $B E = D F = x$ ，分别以 $F C$ 、 $C E$ 为边在长方形 $A B C D$ 外侧作正方形 $C F G H$ 和 $C E M N$ ，若长方形 $C E P F$ 的面积为40，求图中阴影部分的面积和.

查看试题解析
23. 阅读材料后解决问题：
小明遇到下面一个问题：
计算（2+1）（2²+1）（2⁴+1）（2⁸+1）．
经过观察，小明发现如果将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：（2+1）（2²+1）（2⁴+1）（2⁸+1）
=（2+1）（2﹣1）（2²+1）（2⁴+1）（2⁸+1）
=（2²﹣1）（2²+1）（2⁴+1）（2⁸+1）
=（2⁴﹣1）（2⁴+1）（2⁸+1）
=（2⁸﹣1）（2⁸+1）
=2¹⁶﹣1
请你根据小明解决问题的方法，试着解决以下的问题：

(1)、（2+1）（2²+1）（2⁴+1）（2⁸+1）（2¹⁶+1）= ．

(2)、（3+1）（3²+1）（3⁴+1）（3⁸+1）（3¹⁶+1）= ．

(3)、化简：（m+n）（m²+n²）（m⁴+n⁴）（m⁸+n⁸）（m¹⁶+n¹⁶）．

查看试题解析
24. 数学活动课上，老师准备了若干个如图1的三种纸片，A种纸片是边长为a的正方形，B种纸片是边长为b的正方形，C种纸片是长为b，宽为a的长方形.并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形.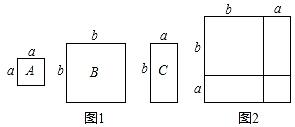

(1)、请用两种不同的方法求图2大正方形的面积：
方法1：；方法2：；

(2)、观察图2，请你写出代数式：（a+b）² ， a²+b² ， ab之间的等量关系；

(3)、根据（2）题中的等量关系，解决如下问题：
①已知：a+b＝5，（a﹣b）²＝13，求ab的值；
②已知（2021﹣a）²+（a﹣2020）²＝5，求（2021﹣a）（a﹣2020）的值.

查看试题解析
25. 在学了乘法公式“(a±b)²= a²±2ab+b²”的应用后，王老师提出问题：求代数式x²＋4x＋5的最小值.要求同学们运用所学知识进行解答.
同学们经过探索、交流和讨论，最后总结出如下解答方法：

解：x²＋4x＋5=x²＋4x+2²-2²+5=(x+2)²+1，

∵(x+2)²≥0，".(x+2)²+1≥1.

当(x+2)²=0时，(x+2)²+1的值最小，最小值是1

∴x²+4x＋5的最小值是1.

请你根据上述方法，解答下列各题：

(1)、直接写出(x-1)²+3的最小值为

(2)、求代数式x²＋10x＋32的最小值.

(3)、若7x-x²+y-11=0，求x＋y的最小值.

查看试题解析
26. 两个边长分别为a、b（a>b）的正方形如图（1）放置，现在取BD的中点P，连接PA、PE，如图（2），把图形分割成三部分，分别标记①、②、③，对应的图形面积分别记为S_①、S_②、S_③.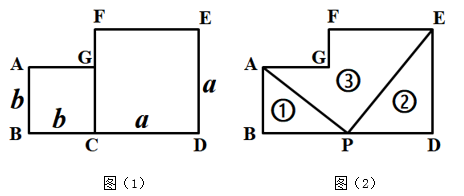

(1)、用字母a、b分别表示S_①、S_②.

(2)、若a-b=2，ab=15，求S_①+S_②.

(3)、若S_①+S_②=3，ab=1，求S_③.

查看试题解析