2023年浙教版数学七年级下学期高分速效复习4 二元一次方程组（进阶版）

试卷更新日期：2023-04-01 类型：复习试卷

进入出卷网下载

一、单选题（每题2分，共20分）

1. 下列方程：①x＋y＝1；② $2 x - \frac{y}{2} = 1$ ；③x²＋y²＝1；④5（x＋y）＝7（x－y）；⑤x²＝1；⑥ $x + \frac{1}{2} = 4$ ，其中是二元一次方程的是（）

A、① B、①②④ C、①③ D、①②④⑥

查看试题解析
2. 在“双减”政策下，王老师把班级里43名学生分成若干小组，每组只能是4人或5人，则分组方案有（）

A、4种 B、3种 C、2种 D、1种

查看试题解析
3. 已知关于 $x$ ， $y$ 的方程组 ${\begin{matrix} x + 3 y = 4 - a \\ x - y = 3 a \end{matrix}$ ，其中 $- 3 \leq a \leq 1$ ，给出下列结论：① ${\begin{matrix} x = 5 \\ y = - 1 \end{matrix}$ 是方程的解；②当 $a = - 2$ 时， $x$ ， $y$ 的值互为相反数；③当 $a = 1$ 时，方程组的解也是方程 $x + y = 4 - a$ 的解；④若 $x \leq 1$ ，则 $1 \leq y \leq 4$ ．其中正确的是（）．

A、①② B、②③ C、②③④ D、①③④

查看试题解析
4. 已知方程组 ${\begin{array}{l} (m + 2) x = 1 \\ 3 x - (m - 3) y^{| m | - 2} + 4 = 0 \end{array}$ 是关于x，y的二元一次方程组，则（）

A、 $m \neq \pm 2$ B、 $m = 3$ C、 $m = - 3$ D、 $m \neq 3$

查看试题解析
5. 若方程组 ${\begin{matrix} 5 a - 3 b = 7 \\ 7 a - 5 b = 3 \end{matrix}$ ，的解为 ${\begin{matrix} a = 6.5 \\ b = 8.5 \end{matrix}$ ，则方程组 ${\begin{matrix} 5 (x - 13) - 3 (y + 1) = 7 \\ 7 (x - 13) - 5 (y + 1) = 3 \end{matrix}$ 的解（）

A、 ${\begin{cases} x = 19.5 \\ y = 9.5 \end{cases}$ B、 ${\begin{cases} x = 19.5 \\ y = 7.5 \end{cases}$ C、 ${\begin{cases} x = - 6.5 \\ y = 9.5 \end{cases}$ D、 ${\begin{cases} x = - 6.5 \\ y = 7.5 \end{cases}$

查看试题解析
6. 我们规定： $[m]$ 表示不超过 $m$ 的最大整数，例如： $[3.1] = 3$ ， $[0] = 0$ ， $[- 3.1] = - 4$ ，则关于 $x$ 和 $y$ 的二元一次方程组 ${\begin{array}{l} [x] + y = 3.2 \\ x - [y] = [3.2] \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 3 \\ y = 0.2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 1.2 \end{array}$ C、 ${\begin{array}{l} x = 3.3 \\ y = 0.2 \end{array}$ D、 ${\begin{array}{l} x = 3.4 \\ y = 0.2 \end{array}$

查看试题解析
7. 已知关于x，y的方程组 ${\begin{array}{l} x + 3 y = 4 - a \\ x - y = 3 a \end{array}$ ，下列结论中正确的有几个（）
①当这个方程组的解x，y的值互为相反数时，a＝－2；②当a＝1时，方程组的解也是方程x＋y＝4＋2a的解；③无论a取什么实数，x＋2y的值始终不变；④若用x表示y，则 $y = - \frac{x}{2} + \frac{3}{2}$ ；

A、1 B、2 C、3 D、4

查看试题解析
8. 已知关于x，y的二元一次方程组 $\{\begin{cases} x + 2 y = a - 3 \\ 3 x - y = 2 a \end{cases}$ ，有下列说法：①当a＝2时，方程的两根互为相反数；②不存在自然数a，使得x，y均为正整数；③x，y满足关系式x－5y＝6；④当且仅当a＝－5时，解得x为y的2倍．其中正确的是（）

A、①②③④ B、①③④ C、②③ D、①②④

查看试题解析
9. 已知有若干片相同的拼图，其形状如图1所示．当4片拼图紧密拼成一列时，总长度为23cm，如图2所示；当10片拼图紧密拼成一列时，总长度为56cm，如图3所示，则图1中的拼图长度为（）

A、5.5cm B、5.6cm C、5.75cm D、6.5cm

查看试题解析
10. 为确保信息安全，信息需要加密传输，发送方由明文→密文（加密），接收方由密文→明文（解密），已知加密规则为：明文a，b，c对应密文a+1，-a+2b+4，b+3c+9，如果接收方收到密文7，12，22，则解密得到的明文为（）

A、6，2，7 B、2，6，7 C、6，7，2 D、7，2，6

查看试题解析

二、填空题（每空3分，共18分）

11. 若关于x、y的方程 $2 x + a y = 7$ 仅有一组正整数解，则满足条件的正整数a的值为．

查看试题解析
12. 已知关于x，y的方程组 ${\begin{array}{l} x - y = 2 a \\ x + 2 y = 3 - a \end{array}$ ，其中 $- 3 \leq a \leq 1$ ，给出下列结论：
①当 $a = - 1$ 时，x，y的值互为相反数；
② ${\begin{array}{l} x = 3 \\ y = - 1 \end{array}$ 是方程组的解；
③无论a取何值，x，y恒有关系式 $x + y = 2$ ；
④若 $x \leq - 1$ ，则 $3 \leq y \leq 4$ ．
其中正确结论的序号是．（把所有正确结论的序号都填上）

查看试题解析
13. 已知关于x，y的方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解为 ${\begin{array}{l} x = 3 \\ y = 4 \end{array}$ ，则关于x，y的方程组 ${\begin{array}{l} 3 a_{1} x + 4 b_{1} y = 5 c_{1} \\ 3 a_{2} x + 4 b_{2} y = 5 c_{2} \end{array}$ 的解为.

查看试题解析
14. 已知 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ 是方程组 ${\begin{array}{l} a x + b y = 3 \\ b x + a y = 7 \end{array}$ 的解，则代数式 $(a + b) (a - b)$ 的值为.

查看试题解析
15. 某超市现有n个人在收银台排队等候结账．设结账人数按固定的速度增加，收银员结账的速度也是固定的．若同时开放2个收银台，需要20分钟可使排队等候人数为0；若同时开放3个收银台，需要12分钟可使排队等候人数为0．为减少顾客等待结账的时间，需要6分钟内使排队等候人数为0，则需要至少同时开放个收银台．

查看试题解析
16. 重庆一中趣味数学社团在社团活动日举办了知识竞答挑战赛.比赛共设置有A、B、C三关，每关设有若干问题，且每关的每个问题分值相同.参赛选手需回答完所有试题，答对得分，答错不扣分.甲、乙、丙三人作答完毕后，结果如下：甲在A、B、C三个关中回答正确的问题数目之比为 $2 ： 1 ： 1$ ，在A关的得分占甲总得分的75%；乙在A、B、C三个关中回答正确的问题数目之比为 $2 ： 5 ： 2$ ，在B关的得分占乙总得分的 $\frac{1}{3}$ ；丙在A关回答正确的问题数目是甲、乙在A关回答正确的问题数目之和的一半，丙在B关回答正确的问题数目比乙在B关回答正确的问题数目少 $\frac{2}{5}$ ，丙与甲在C关回答正确的数目相同，若甲、乙两人的总得分之比为 $48 ： 25$ ，则乙、丙两人的总得分之比为.

查看试题解析

三、计算题（共9分）

17. 解方程组

(1)、 ${\begin{matrix} 5 x + 2 y = - 3 \\ 8 x - 4 y = 9 \end{matrix}$

(2)、 ${\begin{matrix} \frac{x}{2} - \frac{y}{3} = 1 \\ 2 x + 3 y = 17 \end{matrix}$

(3)、 ${\begin{matrix} x + y - z = 0 \\ 2 x - 3 y + 2 z = 5 \\ x + 2 y - z = 3 \end{matrix}$

查看试题解析

四、解答题（共9题，共73分）

18. 甲、乙两班同时从学校 $A$ 出发去距离学校 $75 k m$ 的军营 $B$ 军训，甲班学生步行速度为 $4 k m / h$ ，乙班学生步行速度为 $5 k m / h$ ，学校有一辆汽车，该车空车速度为 $40 k m / h$ ，载人时的速度为 $20 k m / h$ ，且这辆汽车一次恰好只能载一个班的学生，现在要求两个班的学生同时到达军营，问他们至少需要多少时间才能到达？

查看试题解析
19. 定义：若点 $P (m ， n)$ 满足 $a m + b n = c$ ，则称点 $P$ 为关于 $x$ ， $y$ 的二元一次方程 $a x + b y = c$ 的精优点．

(1)、若点 $A (3 ， p)$ 为方程 $2 x - y = 1$ 的精优点，则 $p =$ ；（直接写出答案）

(2)、 $u$ ， $v$ 为正整数，且点 $B (u + v ， 13 - u)$ 为方程 $2 x - y = u - v$ 的精优点．求 $u$ ， $v$ 的值；

(3)、 $m$ ， $s$ ， $t$ ， $k$ 为实数，点 $C (m ， s)$ 与点 $D (2 m + k ， t)$ 都是方程 $2 x + 3 y = 1$ 的精优点，且 $2 s - t = \frac{1}{3} (k^{2} + 2 k - 2)$ ，求 $k$ 的值．

查看试题解析
20. 规定关于x的一元一次方程ax=b的解为 $b - a$ ，则称该方程是“郡园方程”，例如：3x=4.5的解为 $4.5 - 3 = 1.5$ ，则该方程3x=4.5就是“郡园方程”.

(1)、若关于x的一元一次方程2x=m是“郡园方程”，求m的值；

(2)、若关于x的一元一次方程 $2 x = a b + a$ 是“郡园方程”，它的解为a，求a，b的值；

(3)、若关于x的一元一次方程 $2 x = m n + m$ 和 $- 2 x = m n + n$ 都是“郡园方程”，求代数式 ${(m n + m)}^{2} - 9 {(m n + n)}^{2} - 3 (m - n)$ 的值.

查看试题解析
21. 【方法体验】已知方程组 ${\begin{matrix} 2018 x - 2017 y = 20 ， ① \\ 2019 x + 2018 y = 500. ② \end{matrix}$ 求4037x＋y的值．小明同学发现解此方程组代入求值很麻烦!后来他将两个方程直接相加便迅速解决了问题．请你体验一下这种快捷思路，写出具体解题过程：
【方法迁移】根据上面的体验，填空：

已知方程组 ${\begin{array}{l} x + 2 y + 3 z = 10 \\ 4 x + 3 y + 2 z = 15 \end{array}$ 则3x＋y－z＝．

【探究升级】已知方程组 ${\begin{array}{l} x + 2 y + 3 z = 10 \\ 4 x + 3 y + 2 z = 15 \end{array}$ 求－2x＋y＋4z的值．小明凑出

“－2x＋y＋4z＝2•（x＋2y＋3z）＋（－1）•（4x＋3y＋2z）＝20－15＝5”，虽然问题获得解决，但他觉得凑数字很辛苦!他问数学老师丁老师有没有不用凑数字的方法，丁老师提示道：假设－2x＋y＋4z＝m•（x＋2y＋3z）＋n•（4x＋3y＋2z），对照方程两边各项的系数可列出方程组 ${\begin{matrix} m + 4 n = - 2 \\ 2 m + 3 n = 1 \\ 3 m + 2 n = 4 \end{matrix}$ ，它的解就是你凑的数!

根据丁老师的提示，填空：

2x＋5y＋8z＝（x＋2y＋3z）＋（4x＋3y＋2z）

【巩固运用】已知2a－b＋kc＝4，且a＋3b＋2c＝－2，当k为时，8a＋3b－2c为定值，此定值是．（直接写出结果）

查看试题解析
22. 在解决“已知有理数x、y、z满足方程组 ${\begin{array}{l} 2 x + 3 y - z = 5 ① \\ x - 2 y + 3 z = 1 ② \end{array}$ ，求 $4 x + 13 y - 9 z$ 的值”时，小华是这样分析与解答的．
解：由① $\times a$ 得： $2 a x + 3 a y - a z = 5 a$ ③，由② $\times b$ 得： $b x - 2 b y + 3 b z = b$ ④．
③＋④得： $(2 a + b) x + (3 a - 2 b) y + (- a + 3 b) z = 5 a + b$ ⑤．
当 $(2 a + b) x + (3 a - 2 b) y + (- a + 3 b) z = 4 x + 13 y - 9 z$ 时，
即 ${\begin{array}{l} 2 a + b = 4 \\ 3 a - 2 b = 13 \\ - a + 3 b = - 9 \end{array}$ ，解得 ${\begin{array}{l} a = 3 \\ b = - 2 \end{array}$ ．
∴① $\times 3 +$ ② $\times (- 2)$ ，得 $4 x + 13 y - 9 z = 5 \times 3 + 1 \times (- 2) = 13$ ．
请你根据小华的分析过程，解决如下问题：

(1)、若有理数a、b满足 $(3 x + 4 y + 2 z) \times a + (x + 6 y + 5 z) \times b = 12 x + 2 y - 5 z$ ，求a、b的值；

(2)、母亲节将至，小新准备给妈妈购买一束组合鲜花，若购买2枝红花、3枝黄花、1枝粉花共需18元；购买3枝红花、5枝黄花、2枝粉花共需28元．则购买1枝红花、3枝黄花、2枝粉花共需多少元？

查看试题解析
23. 数轴上有两个动点M，N，如果点M始终在点N的左侧，我们称作点M是点N的“追赶点”．如图，数轴上有2个点A，B，它们表示的数分别为-3，1，已知点M是点N的“追赶点”，且M，N表示的数分别为m，n．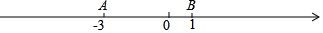

(1)、由题意得：点A是点B的“追赶点”，AB=1-(-3)=4(AB表示线段AB的长，以下相同)；类似的，MN= ．

(2)、在A，M，N三点中，若其中一个点是另外两个点所构成线段的中点，请用含m的代数式来表示n．

(3)、若AM=BN，MN= $\frac{4}{3}$ AM，求m和n值．

查看试题解析
24. 如图1，已知直线AB∥CD，∠CＭＮ＝60°，射线ＭE从ＭD出发，绕点Ｍ以每秒ａ度的速度按逆时针方向旋转，到达ＭC后立即以相同的速度返回，到达ＭD后继续改变方向，继续按上述方式旋转；射线ＮF从ＮA出发，绕点Ｎ以每秒ｂ度的速度按逆时针方向旋转，到达ＮB后停止运动，此时ＭE也同时停止运动．其中ａ，ｂ满足方程组 ${\begin{array}{l} 4 a + b = 17 \\ 3 a - 2 b = 10 \end{array}$

(1)、求ａ，ｂ的值；

(2)、若ＮF先运动30秒，然后ＭE一起运动，设ＭE运动的时间为ｔ，当运动过程中ＭE∥ＮF时，求ｔ的值；

(3)、如图2，若ＭE与ＮF同时开始转动，在ＭE第一次到达ＭC之前，ＭE与ＮF交于点Ｐ，过点Ｐ作ＰＱ⊥ＭE于点Ｐ，交直线AB于点Ｑ，则在运动过程中，若设∠ＮＭE的度数为ｍ，请求出∠ＮＰＱ的度数（结果用含ｍ的代数式表示）．

查看试题解析

25. 水是生命之源，“节约用水，人人有责”.为了加强公民的节水意识，合理利用水资源，某市居民生活用水按阶梯式水价计费，下表是该市居民“一户一表”生活用水及阶梯计费价格表的部分信息（注：水费按月份结算，m³表示立方米）

每户每月用水量（m³）	自来水销售价格（元/m³）	污水处理价格（元/m³）
不超出6m³部分	$a$	1.10
超出6m³不超出10m³的部分	$b$	1.10
超出10m³的部分	7.00	1.10

（注：①每户产生的污水量等于该户自来水用水量；②水费=自来水费用+污水处理费用）.

已知2021年三月份，小红家用水7m³ ，交水费27.2元，小聪家用水9m³ ，交水费38.4元.

(1)、请你根据以上信息，求表中

a

，

b

的值；

(2)、由于七月份正值夏天，小红家预计用水12.5吨，求小红家七月份预计应缴水费多少元？

(3)、若小聪家四、五月份共用水20m³ ，其中四月份的用水量低于五月份的用水量，共缴水费89元，则小聪家四、五月份的用水量各是多少？

查看试题解析

26. 某市为了美化亮化某景点，在两条笔直的景观道MN、QP上，分别放置了A、B两盏激光灯，如图所示，A灯发出的光束自AM逆时针旋转至AN便立即回转；B灯发出的光束自BP逆时针旋转至BQ便立即回转，两灯不间断照射，A灯每秒转动a度，B灯每秒转动b度，且满足 $3^{- b} = \frac{1}{3} ， 2^{3 b - a} = 1$ ，若这两条景观道的道路是平行的，即MN∥QP.

(1)、求a、b的值；

(2)、若B灯先转动10秒，A灯才开始转动：
当A灯转动5秒时，两灯的光束AM′和BP′到达如图①所示的位置，试问AM′和BP′是否平行？请说明理由；

(3)、当B灯光束第一次达到BQ之前，两灯的光束是否能互相垂直，如果能互相垂直，那么此时A灯旋转的时间为秒.（不要求写出解答过程）

查看试题解析