2023年浙教版数学七年级下学期高分速效复习3 二元一次方程组（基础版）

试卷更新日期：2023-04-01 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列各方程是二元一次方程的是（）

A、 $\frac{x - 2}{3} + 2 y = 4$ B、 $3 x y + 9 = 8$ C、 $3 x + \frac{1}{y} = 1$ D、 $x^{2} = 5 y + 1$

查看试题解析
2. 如果 $\{\begin{cases} x = 1 \\ y = - 2 \end{cases}$ 是关于x、y二元一次方程ax＋y＝1的解，那么a＝（）

A、－3 B、－1 C、1 D、3

查看试题解析
3. 下列方程组中，解是 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ 的是（）

A、 ${\begin{array}{l} x + y = 0 \\ x + 2 y = - 1 \end{array}$ B、 ${\begin{array}{l} x - 2 y = 2 \\ x + 2 y = - 1 \end{array}$ C、 ${\begin{array}{l} x - y = 0 \\ x - 2 y = 3 \end{array}$ D、 ${\begin{array}{l} x + y = 0 \\ x - y = - 2 \end{array}$

查看试题解析
4. 二元一次方程组 ${\begin{array}{l} x = 2 y \\ x - y = 4 \end{array}$ 的解为（）．

A、 ${\begin{array}{l} x = 4 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = 8 \\ y = 4 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = 4 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$

查看试题解析
5. 用加减消元法解二元一次方程组 ${\begin{array}{l} x - y = 7 ① \\ 2 x - 3 y = 2 ② \end{array}$ 时，下列能消元的是（）

A、①×2+② B、①×3+② C、①×2-② D、①×（-3）-②

查看试题解析
6. 已知实数x，y，z满足 ${\begin{array}{l} x + y + z = 7 \\ 4 x + y - 2 z = 2 \end{array}$ ，则代数式3(x﹣z)+1的值是（）

A、﹣2 B、﹣4 C、﹣5 D、﹣6

查看试题解析
7. 某车间有90名工人，每人每天平均能生产螺栓15个或螺帽24个，要使一个螺栓配套两个螺帽，应该如何分配工人才能使生产的螺栓和螺帽刚好配套？若设生产螺栓x人，生产螺帽y人，则列方程组得（）

A、 ${\begin{array}{l} x + y = 90 \\ 15 x = 24 y \end{array}$ B、 ${\begin{array}{l} x + y = 90 \\ 15 x = 48 y \end{array}$ C、 ${\begin{array}{l} x + y = 90 \\ 30 x = 24 y \end{array}$ D、 ${\begin{array}{l} x + y = 90 \\ 2 (15 - x) = 24 y \end{array}$

查看试题解析
8. 如图，在数轴上，点 $A$ 、 $B$ 分别表示数 $a$ 、 $b$ ，且 $a + b = 0$ .若 $A B = 4$ ，则点 $A$ 表示的数为（）

A、 $- 4$ B、 $- 2$ C、2 D、4

查看试题解析
9. 6月18日，最开始是京东的周年庆，2013年后，618就成了各大电商平台的网购节了．在618当日，小梦在某电商平台上选择了甲乙丙三种商品，当购物车内选3件甲，2件乙，1件丙时显示价格为420元；当选2件甲，3件乙，4件丙时显示价格为580元，那么购买甲、乙、丙各两件时应该付款（）

A、200元 B、400元 C、500元 D、600元

查看试题解析
10. 如图，大长方形 $A B C D$ 中无重叠地放置9个形状、大小都相同的小长方形，已知大长方形的长与宽的差为2，小长方形的周长为14，则图中空白部分的面积为（）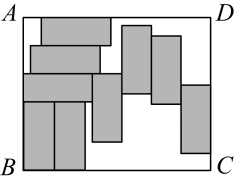

A、143 B、99 C、44 D、53

查看试题解析

二、填空题（每空4分，共24分）

11. 请写出一个解为 ${\begin{matrix} x = 1 \\ y = - 2 \end{matrix}$ 的二元一次方程：.

查看试题解析
12. 已知方程组 ${\begin{cases} (m + 1) x = 2 \\ 3 x - y^{m^{2} - 2} = 1 \end{cases}$ 是二元一次方程组，则m= ．

查看试题解析
13. 已知关于x，y的二元一次方程3x－4y＋mx＋2m＋8＝0，若无论m取任何实数，该二元一次方程都有一个固定的解，则这个固定的解为．

查看试题解析
14. 小华和小盘到校门外文具店买文件，小华购铅笔2支，练习本2本，圆珠笔1支，共付9元钱；小慧购同样铅笔1支，练习本4本，圆珠笔2支，共付12元钱，若小明去买与她们一样的购铅笔1支、练习本2本、圆珠笔1支，他需付元钱.

查看试题解析
15. 某工程队承包了某段全长1800米的过江隧道施工任务，甲、乙两个班组分别从东、西两端同时掘进，已知甲组比乙组平均每天多掘进2米，经过5天施工，两组共掘进了60米，为加快工程进度，通过改进施工技术，在剩余的工程中，甲组平均每天能比原来多掘进2米，乙组平均每天能比原来多掘进1米，按此施工进度，能够比原来少用天完成任务．

查看试题解析
16. 甲、乙二人分别从相距 $20 k m$ 的A，B两地出发，相向而行．右上图是小华绘制的甲、乙二人两次运动的情形，设甲的速度是 $x k m / h$ ，乙的速度是 $y k m / h$ ，根据题意可列的方程组是．

查看试题解析

三、计算题（共2题，共14分）

17. 用指定的方法解下列方程组：

(1)、 $\{\begin{cases} y = 2 x - 3 \\ 3 x + 2 y = 8 \end{cases}$ (代入法)

(2)、 $\{\begin{cases} 3 x + 4 y = 16 \\ 5 x - 6 y = 33 \end{cases}$ (加减法)

查看试题解析
18. 解方程组 ${\begin{array}{l} a + b + c = 6 \\ 3 a - b + c = 4 \\ 2 a + 3 b - c = 12 \end{array}$ ．

查看试题解析

四、解答题（共6题，共52分）

19. 已知 ${\begin{cases} x = - 1 ， \\ y = 2 \end{cases}$ 是关于x、y的二元一次方程 $2 x + a y = 6$ 的一组解，求a的平方根．

查看试题解析
20. 解方程组 ${\begin{array}{l} a x + 2 y = 7 \\ c x - d y = 4 \end{array}$ 时，一学生把a看错后得到 ${\begin{array}{l} x = 5 \\ y = 1 \end{array}$ ，而正确的解是 ${\begin{array}{l} x = 3 \\ y = - 1 \end{array}$ ，求 $\sqrt{a c d}$ 的值．

查看试题解析
21. 已知方程组 ${\begin{array}{l} 3 x - 2 y = 1 \\ a x + b y = 3 \end{array}$ 和 ${\begin{array}{l} a x - b y = 1 \\ 4 x + y = 5 \end{array}$ 有相同的解，求 $a^{2} - 2 a b + b^{2}$ 的值.

查看试题解析
22. 阅读下列材料，然后解答后面的问题.
已知方程组 ${\begin{array}{l} 3 x + 7 y + z = 20 \\ 4 x + 10 y + z = 27 \end{array}$ ，求x+y+z的值.

解：将原方程组整理得 ${\begin{array}{l} 2 (x + 3 y) + (x + y + z) = 20 ① \\ 3 (x + 3 y) + (x + y + z) = 27 ② \end{array}$ ，

②–①，得x+3y=7③，

把③代入①得，x+y+z=6.

仿照上述解法，已知方程组 ${\begin{array}{l} 6 x + 4 y = 22 \\ - x - 6 y + 4 z = - 1 \end{array}$ ，试求x+2y–z的值.

查看试题解析
23. 已知，某医用材料厂商有甲、乙两条口罩生产线，在原有产能下，每天甲生产线比乙生产线少生产56万只，两条生产线3天共生产口罩336万只．

(1)、在原有产能下，求甲、乙两条生产线每天各生产口罩多少万只？

(2)、该厂家收到订单，需要生产840万只口罩，两条生产线同时工作了2天后，该厂家加快了生产速度，又用5天时间完成了全部订单，求提升产能后，该厂家的日产量增加了多少万只？

查看试题解析
24. 今年疫情期间某物流公司计划用两种车型运输救灾物资，已知：用2辆A型车和1辆B型车装满物资一次可运10吨；用1辆A型车和2辆B型车一次可运11吨.某物流公司现有31吨货物资，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都装满.

(1)、1辆A型车和1辆B型车都装满物资一次可分别运多少吨?

(2)、请你帮该物流公司设计租车方案；

(3)、若A型车每辆需租金每次100元，B型车租金每次120元，请选出最省钱的租车方案，并求出最少租车费.

查看试题解析