2023年浙教版数学七年级下学期高分速效复习2 平行线(进阶版)
试卷更新日期:2023-04-01 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 下列各项正确的是( )A、有公共顶点且相等的两个角是对顶角 B、过一点有且只有一条直线与已知直线垂直 C、直线外一点到已知直线的垂线段叫做这点到直线的距离 D、同一平面内,两条直线的位置关系只有相交和平行两种2. 已知n(n≥3,且n为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当n=3时,共有2个交点;当n=4时,共有5个交点;当n=5时,共有9个交点;…依此规律,当共有交点个数为27时,则n的值为( )
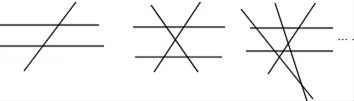 A、6 B、7 C、8 D、93. 下列说法中:①40°35′=2455′;②如果∠A+∠B=180°,那么∠A与∠B互为余角;③经过两点有一条直线,并且只有一条直线;④在同一平面内,不重合的两条直线不是平行就是相交.正确的个数为( ).A、1个 B、2个 C、3个 D、4个4. 如图, 和 不是同旁内角的是( )A、
A、6 B、7 C、8 D、93. 下列说法中:①40°35′=2455′;②如果∠A+∠B=180°,那么∠A与∠B互为余角;③经过两点有一条直线,并且只有一条直线;④在同一平面内,不重合的两条直线不是平行就是相交.正确的个数为( ).A、1个 B、2个 C、3个 D、4个4. 如图, 和 不是同旁内角的是( )A、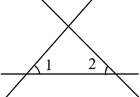 B、
B、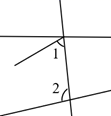 C、
C、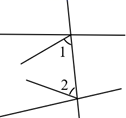 D、
D、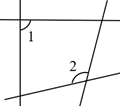 5. 下列说法:①如果∠1+ ∠2+∠3=180°,那么∠1,∠2,∠3三个角互为补角;②如果∠A+ ∠B=90°,那么∠A与∠B互为余角;③“对顶角相等”成立,反之“相等的角是对顶角”也成立;④两条直线被第三条直线所截,同位角相等;⑤两点之间,线段最短. 正确的个数是( )A、2个 B、3个 C、4个 D、5个6. 一辆汽车向前行驶,两次拐弯后,仍在原来的方向上前行,以下可能的情况是( )A、先右拐50°,后左拐130° B、先左拐50°,后右拐50° C、先左拐50°,后左拐130° D、先右拐50°,后右拐50°7. 如图所示,给出下列条件:①∠1=∠B;②∠EFD+∠B=180°;③∠B=∠D;④∠E=∠B;⑤∠BFD=∠B.其中,一定能判断AB∥CD的条件的个数为( )
5. 下列说法:①如果∠1+ ∠2+∠3=180°,那么∠1,∠2,∠3三个角互为补角;②如果∠A+ ∠B=90°,那么∠A与∠B互为余角;③“对顶角相等”成立,反之“相等的角是对顶角”也成立;④两条直线被第三条直线所截,同位角相等;⑤两点之间,线段最短. 正确的个数是( )A、2个 B、3个 C、4个 D、5个6. 一辆汽车向前行驶,两次拐弯后,仍在原来的方向上前行,以下可能的情况是( )A、先右拐50°,后左拐130° B、先左拐50°,后右拐50° C、先左拐50°,后左拐130° D、先右拐50°,后右拐50°7. 如图所示,给出下列条件:①∠1=∠B;②∠EFD+∠B=180°;③∠B=∠D;④∠E=∠B;⑤∠BFD=∠B.其中,一定能判断AB∥CD的条件的个数为( ) A、2个 B、3个 C、4个 D、5个8. 如右图,AB∥CD , PG平分∠EPF , ∠A+∠AHP=180°,下列结论:
A、2个 B、3个 C、4个 D、5个8. 如右图,AB∥CD , PG平分∠EPF , ∠A+∠AHP=180°,下列结论:①CD∥PH;②∠BEP+∠DFP=2∠EPG;③∠FPH=∠GPH;④∠A+∠AGP+∠DFP﹣∠FPG=180°;⑤若∠BEP>∠DFP , 则 =2,
其中正确结论的个数是( )
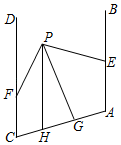 A、2个 B、3个 C、4个 D、5个9. ①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )
A、2个 B、3个 C、4个 D、5个9. ①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )


 A、、1个 B、2个 C、3个 D、4个10. 如图,将三角形ABC向左平移3个单位长度,得到三角形DEF.若四边形ABFD的周长为20个单位长度,则三角形ABC的周长是( )
A、、1个 B、2个 C、3个 D、4个10. 如图,将三角形ABC向左平移3个单位长度,得到三角形DEF.若四边形ABFD的周长为20个单位长度,则三角形ABC的周长是( )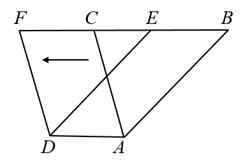 A、17个单位长度 B、14个单位长度 C、11个单位长度 D、8个单位长度
A、17个单位长度 B、14个单位长度 C、11个单位长度 D、8个单位长度二、填空题(每空3分,共18分)
-
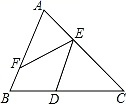
11. 如图,有下列3个结论:①能与∠DEF构成内错角的角的个数是2;②能与∠EFB构成同位角的角的个数是1;③能与∠C构成同旁内角的角的个数是4,以上结论正确的是.
 12. 如图,直线AB,CD被直线CE所截, , 请写出能判定AB∥CD的一个条件: .
12. 如图,直线AB,CD被直线CE所截, , 请写出能判定AB∥CD的一个条件: . 13. 如图,直线a,b与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠3=180°,其中能判断ab的是(填序号).
13. 如图,直线a,b与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠3=180°,其中能判断ab的是(填序号).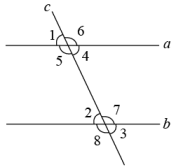 14. 如图, ∥ ,点 , 分别是 , 上的一点,射线 绕点 顺时针旋转,速度为每秒 度,射线 绕点 顺时针旋转,速度为每秒 度,旋转至与 重合便立即回转,当射线 旋转至与 重合时, 与 都停止转动.若射线 先转动 秒,射线 才开始转动,则射线 转动秒后, 与 平行.
14. 如图, ∥ ,点 , 分别是 , 上的一点,射线 绕点 顺时针旋转,速度为每秒 度,射线 绕点 顺时针旋转,速度为每秒 度,旋转至与 重合便立即回转,当射线 旋转至与 重合时, 与 都停止转动.若射线 先转动 秒,射线 才开始转动,则射线 转动秒后, 与 平行. 15. 已知∠ABG为锐角,AH∥BG,点C从点B(点C不与点B重合)出发,沿射线BG的方向移动,CD∥AB交直线AH于点D,CE⊥CD交AB于点E,CF⊥AD,垂足为点F(点F不与点A重合).若∠ECF=n°,则∠BAF=.(用n来表示)16. 如图,Rt△AOB的周长为100,在其内部有n个小直角三角形,则这n个小直角三角形的周长之和为
15. 已知∠ABG为锐角,AH∥BG,点C从点B(点C不与点B重合)出发,沿射线BG的方向移动,CD∥AB交直线AH于点D,CE⊥CD交AB于点E,CF⊥AD,垂足为点F(点F不与点A重合).若∠ECF=n°,则∠BAF=.(用n来表示)16. 如图,Rt△AOB的周长为100,在其内部有n个小直角三角形,则这n个小直角三角形的周长之和为
三、作图题(共2题,共15分)
-
17. 用直尺和圆规作图,不写作法,保留作图痕迹.
一辆货车由点A出发沿山路送货,在点B和点C两次转弯后,保持与出发时相同的方向,且点C到终点D的距离与点B到点C的距离相等,请根据所给条件,确定点D的位置.
 18. 如图,在每个小正方形边长为1的方格纸中,△ 的顶点都在方格纸格点上.将△ 向左平移2格,再向上平移4格.
18. 如图,在每个小正方形边长为1的方格纸中,△ 的顶点都在方格纸格点上.将△ 向左平移2格,再向上平移4格.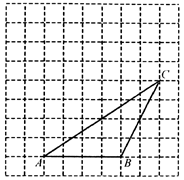 (1)、请在图中画出平移后的△ ;(2)、图中AC和A′C′的关系;(3)、再在图中画出△ 的高 ;(4)、 =;(5)、在图中能使 的格点 的个数有个(点 异于C).
(1)、请在图中画出平移后的△ ;(2)、图中AC和A′C′的关系;(3)、再在图中画出△ 的高 ;(4)、 =;(5)、在图中能使 的格点 的个数有个(点 异于C).四、解答题(共6题,共57分)
-
19. 如图1,已知AB∥CD,∠B=20°,∠D=110°.
 (1)、若∠E=50°,请直接写出∠F的度数;(2)、探索∠E与∠F之间满足的数量关系,并说明理由;(3)、如图2,EP平分∠BEF,FG平分∠EFD,FG的反向延长线交EP于点P,求∠P的度数.20. 在一次数学综合实践活动课上,同学们进行了如下探究活动:将一块等腰直角三角板的顶点G放置在直线上,旋转三角板.
(1)、若∠E=50°,请直接写出∠F的度数;(2)、探索∠E与∠F之间满足的数量关系,并说明理由;(3)、如图2,EP平分∠BEF,FG平分∠EFD,FG的反向延长线交EP于点P,求∠P的度数.20. 在一次数学综合实践活动课上,同学们进行了如下探究活动:将一块等腰直角三角板的顶点G放置在直线上,旋转三角板.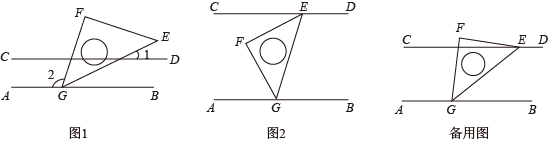 (1)、如图1,在边上任取一点P(不同于点G,E),过点P作 , 若 , 求的度数;(2)、如图2,过点E作 , 请探索并说明与之间的数量关系;(3)、将三角板绕顶点G转动,过点E作 , 并保持点E在直线的上方.在旋转过程中,探索与之间的数量关系,并说明理由.21. 点E在射线DA上,点F、G为射线BC上两个动点,满足 , , DG平分∠BDE.
(1)、如图1,在边上任取一点P(不同于点G,E),过点P作 , 若 , 求的度数;(2)、如图2,过点E作 , 请探索并说明与之间的数量关系;(3)、将三角板绕顶点G转动,过点E作 , 并保持点E在直线的上方.在旋转过程中,探索与之间的数量关系,并说明理由.21. 点E在射线DA上,点F、G为射线BC上两个动点,满足 , , DG平分∠BDE. (1)、如图1,当点G在F右侧时,求证:;(2)、如图2,当点G在F左侧时,求证:;(3)、如图3,在(2)的条件下,P为BD延长线上一点,DM平分∠BDG,交BC于点M,DN平分∠PDM,交EF于点N,连接NG,若 , , 则∠DBF的度数为 .22. 阅读理解:如图 , 已知点是外一点,连接 , 求的度数.
(1)、如图1,当点G在F右侧时,求证:;(2)、如图2,当点G在F左侧时,求证:;(3)、如图3,在(2)的条件下,P为BD延长线上一点,DM平分∠BDG,交BC于点M,DN平分∠PDM,交EF于点N,连接NG,若 , , 则∠DBF的度数为 .22. 阅读理解:如图 , 已知点是外一点,连接 , 求的度数.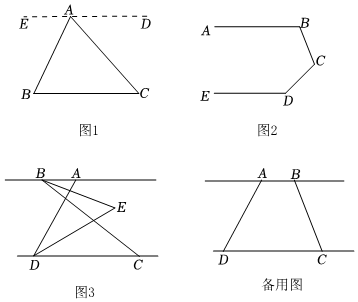 (1)、阅读并补充下面推理过程.
(1)、阅读并补充下面推理过程.解:过点作 , , .
.
.
解题反思:从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将 , , “凑”在一起,得出角之间的关系,使问题得以解决.
(2)、方法运用:如图2,已知 , 求的度数.(3)、深化拓展:如图3,已知 , 点在点的右侧, , 平分 , 点是直线上的一个动点(不与点重合), , 平分 , , 所在的直线交于点 , 点在与两条平行线之间.若 , 请你直接写出的度数.(用含的代数式表示).23. 阅读下面材料:小亮同学遇到这样一个问题:
已知:如图甲,ABCD,E为AB,CD之间一点,连接BE,DE,得到∠BED.

求证:∠BED=∠B+∠D.
(1)、小亮写出了该问题的证明,请你帮他把证明过程补充完整.证明:过点E作EFAB,
则有∠BEF= ▲ .
∵ABCD,
∴ ▲ ▲ ,
∴∠FED= ▲ .
∴∠BED=∠BEF+∠FED=∠B+∠D.
(2)、请你参考小亮思考问题的方法,解决问题:如图乙,已知:直线ab,点A,B在直线a上,点C,D在直线b上,连接AD,BC,BE平分∠ABC,DE平分∠ADC,且BE,DE所在的直线交于点E.
①如图1,当点B在点A的左侧时,若∠ABC=60°,∠ADC=70°,求∠BED的度数;
②如图2,当点B在点A的右侧时,设∠ABC=α,∠ADC=β,请你求出∠BED的度数(用含有α,β的式子表示).
24. 如图,已知射线 ,连接 ,点 是射线 上的一个动点(与点 不重合), , 分别平分 和 ,分别交射线 于点 , . (1)、当 时,求 的度数.(2)、不断改变 的度数, 与 却始终存在某种数量关系,设 ,用含 的式子表示 的度数为 ;(3)、某同学利用量角器量出 和 的度数后,探究二者之间的数量关系.他惊奇地发现,当点 在射线 上运动时,无论点 在 上的什么位置, 与 之间的数量关系都保持不变,请写出它们的关系,并说明理由.
(1)、当 时,求 的度数.(2)、不断改变 的度数, 与 却始终存在某种数量关系,设 ,用含 的式子表示 的度数为 ;(3)、某同学利用量角器量出 和 的度数后,探究二者之间的数量关系.他惊奇地发现,当点 在射线 上运动时,无论点 在 上的什么位置, 与 之间的数量关系都保持不变,请写出它们的关系,并说明理由.