2023年浙教版数学七年级下学期高分速效复习1 平行线（基础版）

试卷更新日期：2023-04-01 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 在如下所示的条件中，可以判断两条直线互相垂直的是（）
①两直线相交所成的四个角都是直角；②两直线相交，对顶角互补；③两直线相交所成的四个角都相等．

A、①② B、①③ C、②③ D、①②③

查看试题解析
2. 三条直线a、b、C，若a∥c，b∥c，则a与b的位置关系是（）

A、a⊥b B、a∥b C、a⊥b或a∥b D、无法确定

查看试题解析
3. 下列现象中，不属于平移的是（）

A、滑雪运动员在平坦的雪地上沿直线滑行 B、时针的走动 C、商场自动扶梯上顾客的升降运动 D、火车在笔直的铁轨上行驶

查看试题解析
4. 如下图，直线AD、BE被直线BF和AC所截，下列说法正确的是（）

A、∠3与∠4是同旁内角 B、∠2与∠5是同位角 C、∠6与∠1是内错角 D、∠2与∠6是同旁内角

查看试题解析
5. 下列说法错误的是（）

A、对顶角相等 B、同位角相等 C、同角的余角相等 D、同角的补角相等

查看试题解析
6. 如图，∠1和∠2是同位角的是（）.

A、 B、 C、 D、

查看试题解析
7. 如下图，下列条件能判断两直线AB，CD平行的是（）

A、∠1＝∠2 B、∠3＝∠4 C、∠1＝∠5 D、∠3＝∠5

查看试题解析
8. 如图，给出了过直线外一点作已知直线的平行线的方法，其依据是（）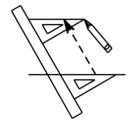

A、两直线平行，同旁内角相等 B、内错角相等，两直线平行 C、同旁内角互补，两直线平行 D、同位角相等，两直线平行

查看试题解析
9. 如图，AB∥CD，CB平分∠ABD．若∠C＝40°，则∠D的度数为（）

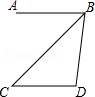A、90° B、100° C、110° D、120°

查看试题解析
10. 下列图形中，根据 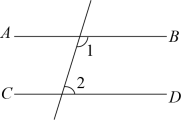$A B ∥ C D$ ，能得到 $∠ 1 = ∠ 2$ 的是（）

A、 B、 C、 D、

查看试题解析

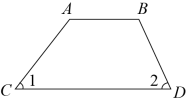
二、填空题（每空3分，共24分）

11. 下列说法中：①在同一平面内，不相交的两条直线叫做平行线；②经过三点一定能画出三条直线；③如果两个角相等，那么这两个角是对顶角；④点C是直线 $A B$ 上的点，如果 $A C = \frac{1}{2} A B$ ，则点C为 $A B$ 的中点.其中正确的有.（填序号）

查看试题解析
12. 如图，AB与BC被AD所截得的内错角是；DE与AC被直线AD所截得的内错角是；图中∠4的内错角是．

查看试题解析
13. 如图，在图中标注的∠1、∠3、∠4、∠5中，当∠2 =∠时， AE∥BF.

查看试题解析
14. 如图，△ABC沿着由点B到点E的方向平移，得到△DEF，若BC＝4，EC＝1，那么平移的距离是．

查看试题解析
15. 如图，把一块直角三角板的直角顶点放在直尺的一边上，如果 $∠ 1 = 30 °$ ，那么 $∠ 2$ 的度数为.

查看试题解析
16. 生活中常见的探照灯、汽车大灯等灯具都是凹面镜.如图，从光源P点照射到凹面镜上的光线 $P A$ 、 $P B$ 等反射以后沿着与直线 $P F$ 平行的方向射出.若 $∠ C A P = 35 °$ ， $∠ D B P = 55 °$ ，则 $∠ A P B =$ °.

查看试题解析

三、作图题（共2题，共10分）

17. 如图1，数学课上，老师在黑板上画出两条直线a，b，两条直线所成的角跑到黑板外面去了．老师让小明在黑板上测量出直线a，b所成的角的度数，他该怎么办？请在图2中画出测量示意图，简要说明画图方法和理由．

查看试题解析
18. 如图，经过平移，四边形 $A B C D$ 的顶点A移到点 $A^{'}$ ，作出平移后的四边形 $A^{'} B^{'} C^{'} D^{'}$ ．

查看试题解析

四、解答题（共7题，共56分）

19. 已知：如图， $∠ A O B$ 和 $O B$ 上的一点P.

(1)、求作直线 $M N$ ，使直线 $M N$ 过点P且 $M N ∥ O A$ ；

(2)、写出一对相等的同位角和一对互补的同旁内角.

查看试题解析
20. 如图所示，已知在 $△ A B C$ 中， $B C = 4 c m$ ，把 $△ A B C$ 沿 $B C$ 方向平移 $2 c m$ 得到 $△ D E F$ 问∶

(1)、图中与 $∠ A$ 相等的角有多少个？

(2)、图中的平行线共有多少对？请分别写出来.

(3)、 $B E ： B C ： B F$ 的值是多少？

查看试题解析
21. 请把下列的证明过程补充完整：
已知：如图，∠1+∠2＝180°，∠A＝∠D，求证：AB∥CD，

证明：∵∠1与∠CGD是对顶角，

∴∠1＝∠CGD（        ）．

又∵∠1+∠2＝180°（已知）．

∴∠CGD+∠2＝180°，

∴AE∥FD（        ），

∴∠A＝∠BFD（        ）．

∵∠A＝∠D（已知），

∴∠BFD＝∠D（        ），

∴AB∥CD（        ）．

查看试题解析
22. 已知：如图，∠B＋∠3＝90°，∠B＋∠E＝90°，∠1＝∠E，求证：AD平分∠BAC，
请完善证明过程，并在括号内填上相应依据：

证明：∵∠B＋∠3＝90°，∠B＋∠E＝90°，（        ）

∴▲ ＝▲ ，（        ）

∴ $A D ∥ E G$ ，（         ）

∴∠2＝∠1，（         ）

∵∠E＝∠1（已知），

∴▲ ＝▲ ，（         ）

∴AD平分∠BAC．（        ）

查看试题解析
23. 已知，如图，BCE、AFE是直线，AB∥CD，∠1=∠2，∠3=∠4。求证：AD∥BE。

证明：∵AB∥CD（已知）

∴∠4=∠ ▲ （                     ）

∵∠3=∠4（已知）

∴∠3=∠ ▲ （                       ）

∵∠1=∠2（已知）

∴∠1+∠CAF=∠2+∠CAF（                     ）

即∠ ▲ =∠ ▲

∴∠3=∠ ▲ （                    ）

∴AD∥BE（                    ）

查看试题解析
24. 如图，点B，C在线段AD的异侧，点E，F分别是线段AB，CD上的点，已知∠1＝∠2，∠3＝∠C．

(1)、求证：AB∥CD；

(2)、若∠2+∠4＝180°，求证：∠BFC+∠C＝180°；

(3)、在（2）的条件下，若∠BFC-30°＝2∠1，求∠B的度数．

查看试题解析
25. 已知：点C是∠AOB的OA边上一点（点C不与点O重合），点D是∠AOB内部一点，射线CD不与OB相交．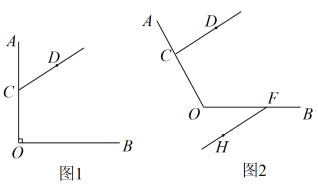

(1)、如图1，∠AOB＝90°，∠OCD＝120°，过点O作射线OE，使得OE//CD．（其中点E在∠AOB内部）．
①依据题意，补全图1；
②直接写出∠BOE的度数．

(2)、如图2，点F是射线OB上一点，且点F不与点O重合，当 $∠ A O B = α (0 ° < α \leq 180 °)$ 时，过点F作射线FH，使得FH//CD（其中点H在∠AOB的外部），用含 $α$ 的代数式表示∠OCD与∠BFH的数量关系，并证明．

查看试题解析