2023年浙教版八年级下学期数学期中模拟卷（4）

试卷更新日期：2023-04-01 类型：期中考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列根式中，不是最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{10}$ C、 $\sqrt{6}$ D、 $\sqrt{2}$

查看试题解析
2. 下列方程中，属于一元二次方程的是（）

A、x²＋3y＝1 B、x²＋3x＝1 C、ax²＋bx＋c＝2 D、 $\frac{1}{x^{2}} + \frac{1}{x} = 1$

查看试题解析
3. 随着我国综合国力的增强，人们生活水平也不断提升，越来越多的人开始关注健康、锻炼身体．其中走路是最简单的锻炼方法之一，舒适的运动鞋就成为走路锻炼的必要装备．运动鞋的鞋底柔软而富有弹性，能起到一定的缓冲作用，防止脚踝受伤．某运动鞋品牌店试销一种新款男鞋，试销期间销售情况如下表：
鞋的尺码/ $c m$
24
24.5
25
25.5
26
26.5
销售量/双
3
8
16
10
6
2
父亲节来临之际，该品牌店店主为了促销再次进货，此次进货应参考的是试销期间所售出鞋的尺码的（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
4. 如果一个多边形的内角和等于一个三角形的外角和的两倍，那么这个多边形是（）

A、三角形 B、四边形 C、五边形 D、六边形

查看试题解析
5. 如图， $▱ A B C D$ 的周长为 $36 c m$ ， $△ A B C$ 的周长为 $28 c m$ ，则对角线 $A C$ 的长为（）

A、 $8 c m$ B、 $9 c m$ C、 $10 c m$ D、 $12 c m$

查看试题解析
6. 某农业基地现有杂交水稻种植面积36公顷，计划两年后将杂交水稻种植面积增加到48公顷，设该农业基地杂交水稻种植面积的年平均增长率为x，则可列方程为（）

A、 $48 (1 + x)^{2} = 36$ B、 $48 (1 - x)^{2} = 36$ C、 $36 (1 + x)^{2} = 48$ D、 $36 (1 - x)^{2} = 48$

查看试题解析
7. 用配方法解一元二次方程 $x^{2} + 8 x - 3 = 0$ ，配方后得到的方程是（）

A、 ${(x + 4)}^{2} = 19$ B、 ${(x - 4)}^{2} = 19$ C、 ${(x - 4)}^{2} = 13$ D、 ${(x + 4)}^{2} = 13$

查看试题解析
8. 实数a，b在数轴上对应点的位置如图所示，化简 $| a | + \sqrt{{(a - b)}^{2}}$ 的结果是：（）

A、 $- 2 a + b$ B、 $2 a - b$ C、 $- b$ D、b

查看试题解析
9. 有关于x的两个方程：ax²+bx+c=0与ax²-bx+c=0，其中abc＞0，下列判断正确的是（）

A、两个方程可能一个有实数根，另一个没有实数根 B、若两个方程都有实数根，则必有一根互为相反数 C、若两个方程都有实数根，则必有一根相等 D、若两个方程都有实数根，则必有一根互为倒数

查看试题解析
10. 如图，平行四边形ABCD中，对角线AC、BD相交于O，BD=2AD，E，F，G分别是OC，OD，AB的中点，下列结论：①四边形BEFG是平行四边形；②BE⊥AC；③EG=FG；④EA平分∠GEF。其中正确的是（）

A、①② B、①②③ C、①②④ D、①③④

查看试题解析

二、填空题（每空3分，共36分）

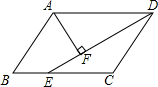
11. 函数 $y = \frac{\sqrt{2 - x}}{x - 1}$ 的自变量 $x$ 的取值范围是．

查看试题解析
12. 如图，在平行四边形ABCD中，DE平分∠ADC交BC于E，AF⊥DE于F，已知∠DAF＝58°，则∠B＝．

查看试题解析
13. “共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献．全球共有40多个国家引种杂交水稻，中国境外种植面积达800万公顷．某村引进了甲、乙两种超级杂交水稻品种，在条件（肥力、日照、通风……）不同的6块试验田中同时播种并核定亩产，统计结果为： ${\bar{x}}_{甲} = 1042 k g$ /亩， $s_{甲}^{2} = 6.5$ ﹐ ${\bar{x}}_{乙} = 1042 k g$ /亩， $s_{乙}^{2} = 1.2$ ，则品种更适合在该村推广．（填“甲”或“乙”）

查看试题解析
14. 数据 $x_{1} ， x_{2} ， x_{3} ， x_{4}$ 的平均数是4，方差是3，则数据 $x_{1} + 1 ， x_{2} + 1 ， x_{3} + 1 ， x_{4} + 1$ 的平均数和方差分别是，．

查看试题解析
15. 如果关于x的一元二次方程 $a x^{2} + b x - 1 = 0$ 的一个解是 $x = 1$ ，则2023-a-b= ．

查看试题解析
16. 如图， $▱ A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O， $O E ⊥ B D$ 交 $A D$ 于点E，连接 $B E$ ，若 $△ A B E$ 的周长为15，则 $▱ A B C D$ 的周长为．

查看试题解析
17. 若一元二次方程ax²=b，当ab>0时的两个根分别是m+1与2m-4，则m=；当ab0时，一元二次方程ax²=b没有实数解.

查看试题解析
18. 如图，在宽为20m，长为32m的矩形地面上修筑同样宽的道路，余下的部分种上草坪，要使草坪的面积为540m² ，求道路的宽若设道路宽为xm，则根据题意可列方程为

查看试题解析
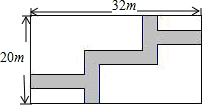19. 如图，▱ABCD中，AC，BD交于O，AE平分∠BAD，EC＝CD＝1，∠ECD＝2∠CDA.下列结论：①AC平分∠EAD；②OE＝ $\frac{1}{4}$ AD；③BD＝ $\sqrt{7}$ ；④S▱ABCD＝ $\sqrt{3}$ .正确的有个.

查看试题解析
20. 已知关于x的方程x²－(k+2)x+2k=0，若等腰三角形ABC的一边长a=1，另外两边长b，c恰好是这个方程的两个根，则△ABC的周长为．

查看试题解析

三、解答题（共6题，共54分）

21. 计算下列各题

(1)、 $2 \sqrt{12} - 9 \sqrt{\frac{1}{3}} + \sqrt{27}$

(2)、 $(\sqrt{3} + 2) (3 - \sqrt{3}) + {(\sqrt{3} + 1)}^{2}$

查看试题解析
22. 解方程：

(1)、 $x^{2} + 2 x = 0$ ；

(2)、 $x^{2} - 6 x + 2 = 0$ ．

查看试题解析
23. 2022年5月25、26日国家实施义务教育质量监测．监测部门从某校八年级全体学生中任意抽取40名学生，平均分成甲、乙两个小组参加艺术测试．根据测试成绩绘制出如下的统计表和统计图（成绩均为整数，满分为10分）．
甲组成绩统计表
成绩
7
8
9
10
人数
3
9
3
5
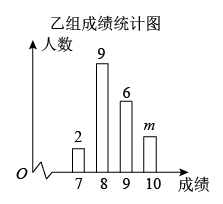
请根据上面的信息，解答下列问题：

(1)、 $m =$ ，甲组成绩的众数是；乙组成绩的中位数是．

(2)、请你计算出甲组的平均成绩．

(3)、已知甲组成绩的方差 $S_{甲}^{2} = 1.05$ ，乙组的平均成绩是8.5，请计算出乙组成绩的方差，并判断哪个小组的成绩更均衡？

查看试题解析
24. 某大型电子商场销售某种空调，每台进货价为2500元，标价为3200元．

(1)、若电子商场连续两次降价，每次降价的百分率相同，最后以2592元售出，求每次降价的百分率；

(2)、市场调研表明：当每台售价为3000元时，平均每天能售出10台，当每台售价每降100元时，平均每天就能多售出4台，若商场要想使这种空调的销售利润平均每天达到5400元，且顾客得到优惠，则每台空调的定价应为多少元？

查看试题解析
25. 如图，平行四边形 $A B C D$ 的周长为36，BD=12，点 $O$ 是对角线AC、BD的交点，点 $E$ 是边 $C D$ 的中点，点 $E F ∥ A C$ 交 $B C$ 的延长线于 $F$ ．

(1)、求证：四边形OCFE是平行四边形；

(2)、求△DOE的周长．

查看试题解析
26. 综合与实践
已知线段AD向下平移m个单位后，再向右平移n个单位至线段BC，点A，D的对应点分别为点B、C，连接AB、CD、AC、BD，AC与BD交于O点．

(1)、如图1，求证：OB=OD．

(2)、如图2，过D点作DM⊥BC于M，N为CD的中点，连接MN，若∠ADB=45°， $O D = 3 \sqrt{2}$ ， MN=4，求 $\frac{B M}{M C}$ 的值．

(3)、在（2）的条件下，H在BC上移动，当 $△ C D H$ 为等腰三角形时，请直接写出HC的长．

查看试题解析

鞋的尺码/ $c m$	24	24.5	25	25.5	26	26.5
销售量/双	3	8	16	10	6	2

成绩	7	8	9	10
人数	3	9	3	5