2023年浙教版八年级下学期数学期中模拟卷（3）

试卷更新日期：2023-04-01 类型：期中考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列方程是关于x的一元二次方程的是（）

A、 $x^{2} + \frac{1}{x} = 1$ B、 $a x^{2} + b x + c = 0$ C、 $(x + 1) (x + 2) = 1$ D、 $(x - 3)^{2} + 4 = x^{2}$

查看试题解析
2. 函数 $y = \sqrt{x + 2}$ 中自变量 $x$ 的取值范围是（）

A、 $x > 2$ B、 $x \geq - 2$ C、 $x < 2$ D、 $x ≤ - 2$

查看试题解析
3. 下列二次根式中，最简二次根式是（）．

A、 $\sqrt{\frac{1}{6}}$ B、 $\sqrt{6}$ C、 $\sqrt{12}$ D、 $\sqrt{36}$

查看试题解析
4. 为了增强学生的安全意识，某校组织学生开展了安全知识竞赛活动，经过一轮初赛后，共有21人进入决赛，本次活动将按照决赛分数评出一等奖2名，二等奖3名，三等奖5名．小丽进入了决寨，要判断自己能否获奖，她应当关注决赛分数的（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
5. 已知m是一元二次方程 $x^{2} - x - 3 = 0$ 的一个根，则 2022-m²+m的值为（）

A、2019 B、2020 C、2023 D、2025

查看试题解析
6. 如图，平行四边形ABCD的对角线AC与BD相交于点O，AB⊥AC．若AC＝6，BD＝10，则AB的长是（）

A、3 B、4 C、5 D、6

查看试题解析
7. 用配方法解一元二次方程 $y^{2} - y - \frac{1}{2} = 0$ 时，下列变形正确的是（）

A、 ${(y + \frac{1}{2})}^{2} = 1$ B、 ${(y - \frac{1}{2})}^{2} = \frac{3}{4}$ C、 ${(y + \frac{1}{2})}^{2} = \frac{3}{4}$ D、 ${(y - \frac{1}{2})}^{2} = 1$

查看试题解析
8. 电影《长津湖》讲述了一段波澜壮阔的历史，自上映以来，全国票房连创佳绩．据不完全统计，某市第一天票房收入约 $2$ 亿元，第三天票房收入约达到 $4$ 亿元，设票房收入每天平均增长率为 $x$ ，下面所列方程正确的是（）

A、 $2 (1 + x)^{2} = 4$ B、 $2 (1 + 2 x) = 4$ C、 $2 (1 - x)^{2} = 4$ D、 $2 + 2 (1 + x) + 2 (1 + x)^{2} = 4$

查看试题解析
9. 如图，①是我国古代建筑中的一种窗格，其中冰裂纹图案象征着竖冰出现裂纹并开始消融，形状无一定规律，代表一种自然和谐美.图②是从图①的冰裂纹窗格图案中提取的由五条线段组成的图形，则∠1+∠2+∠3+∠4+∠5=（）

A、72° B、108° C、360° D、540°

查看试题解析
10. 如图，在给定的△ABC中，动点D从点B出发沿BC方向向终点C运动，DE $∥$ AC交AB于点E，DF $∥$ AB交AC于点F，O是EF的中点，在整个运动过程中，△OBC的面积的大小变化情况是（）

A、不变 B、一直增大 C、先增大后减小 D、先减小后增大

查看试题解析

二、填空题（每空4分，共32分）

11. 化简＝．

查看试题解析
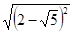12. 若关于x的一元二次方程 $(a - 5) x^{2} - 6 x + 3 = 0$ （a是常数）有实根，那么a的取值范围是．

查看试题解析
13. 在平行四边形ABCD中，有两个内角的度数比为1：5，则平行四边形ABCD中较小内角的度数为．

查看试题解析
14. 将一组数据中的每一个数减去30后，得到新的一组数据的平均数是6，则原来这组数据的平均数是；

查看试题解析
15. 要使 $n$ 和 $\sqrt{45 n}$ 都是正整数，则 $n$ 最小为．

查看试题解析
16. 如图，点E是▱ABCD的对角线BD上一点，连接CE，若点E在线段AD的垂直平分线上，点D在线段EC的垂直平分线上，且∠DCE=66°，则∠ADB= ．

查看试题解析
17. 已知关于一元二次方程ax²＋bx＋c＝0(a≠0)，有下列说法：
①若a－b＋c＝0则b²－4ac≥0；②若方程ax²＋bx＋c＝0两根为1和2，则2a－c＝0；③若方程ax²＋c＝0有两个不相等的实根，则方程ax²＋bx＋c＝0必有实根；④若b＝2a＋c，则方程有两个不相等的实数根．

其中正确的是． (填写序号)

查看试题解析
18. 用硬纸板剪一个平行四边形ABCD，作出它的对角线的交点O，我们可以做如下操作：
用大头针把一根平放在平行四边形上的直细木条固定在点O处，并使细木条可以绕点O转动，拨动细木条，它可以停留在任意位置. 如果设细木条与一组对边AB，CD的交点分别为点E，F，则下列结论：①OE=OF；②AE=CF；③BE=DF；④△AOE≌△COF，其中一定成立的是（填写序号即可）.

查看试题解析

三、解答题（共6题，共58分）

19. 计算：

(1)、 $\sqrt{48} - \sqrt{12} + \sqrt{27}$ ；

(2)、 $(2 \sqrt{6} + \sqrt{\frac{2}{3}}) \times \sqrt{3}$ ．

查看试题解析
20. 解下列一元二次方程：

(1)、3x²＝9x

(2)、x²－4x－1＝0

查看试题解析
21. 为进一步宣传防震减灾科普知识，增强学生应急避险和自救互救能力，某校组织七、八年级各200名学生进行“防震减灾知识测试”（满分100分）．现分别在七，八年级中各随机抽取10名学生的测试成绩x（单位：分）进行统计、整理如下：
七年级：86，90，79，84，74，93，76，81，90，87．
八年级：85，76，90，81，84，92，81，84，83，84．
七八年级测试成绩频数统计表

$70 \leq x < 80$
$80 \leq x < 90$
$90 \leq x \leq 100$
七年级
3
4
3
八年级
1
7
a
七八年级测试成绩分析统计表

平均数
中位数
众数
方差
七年级
84
b
90
36.4
八年级
84
84
c
18.4
根据以上信息，解答下列问题：

(1)、a= ， b= ， c=；

(2)、规定分数不低于85分记为“优秀”，估计这两个年级测试成绩达到“优秀”的学生人数；

(3)、你认为哪个年级的学生掌握防震减灾科普知识的总体水平较好？请说明理由．

查看试题解析
22. 如图，用硬纸板剪一个平行四边形ABCD，找到对角线交点O，用大头针在点O处将一根平放在平行四边形上的细直木条固定，并使细木条可以绕点O转动，拨动细木条，可随意停留在任意位置．

(1)、木条把平行四边形ABCD分成了两部分，在拨动细木条的过程中，两部分的面积是否始终相等？答：（填“是”或“否”）；

(2)、木条与▱ABCD的边AD，BC相交于点E，F．
①请判断OE与OF是否始终相等，并说明理由；
②以A，E，C，F为顶点的四边形是平行四边形吗？为什么？

查看试题解析
23. 为了有效预防和控制疫情，及时监测疫情发展态势，实施定期核酸检测。某社区准备搭建一个动态核酸检测点，现有33米可移动的隔离带，搭围成如图的临时检测点，这是一个一面靠墙（墙面为AE）的矩形，内部分成两个区，M区为登记区，N区为检测区，入口通道在BC边上，两区通道在CD边上，出口通道在EF边上，通道宽均为1米。

(1)、若设AB=x，则BF可表示为；

(2)、问所围成矩形ABFE的面积能否达到96平方米？如果能，求出AB的长；如果不能，说明理由；

(3)、检测点使用一天后，发现检测点面积需要扩大，问现有的33米隔离带，能否围出147平方米的面积?如果能，请说明理由；如果不能，在搭围方法不变的情况下，则至少需要增加多少米隔离带，恰好能围成147平方米？

查看试题解析
24. 如图，已知一次函数y=﹣ $\frac{1}{2}$ x+b的图象过点A（0，3），点p是该直线上的一个动点，过点P分别作PM垂直x轴于点M，PN垂直y轴于点N，在四边形PMON上分别截取：PC= $\frac{1}{3}$ MP，MB= $\frac{1}{3}$ OM，OE= $\frac{1}{3}$ ON，ND= $\frac{1}{3}$ NP．

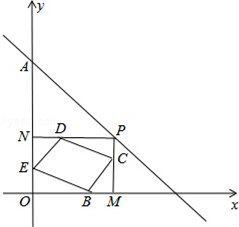(1)、b=；

(2)、求证：四边形BCDE是平行四边形；

(3)、在直线y=﹣ $\frac{1}{2}$ x+b上是否存在这样的点P，使四边形BCDE为正方形？若存在，请求出所有符合的点P的坐标；若不存在，请说明理由．

查看试题解析

	$70 \leq x < 80$	$80 \leq x < 90$	$90 \leq x \leq 100$
七年级	3	4	3
八年级	1	7	a

	平均数	中位数	众数	方差
七年级	84	b	90	36.4
八年级	84	84	c	18.4