2023年浙教版八年级下学期数学期中模拟卷（1）

试卷更新日期：2023-04-01 类型：期中考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列二次根式中属于最简二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{\frac{3}{2}}$ C、 $\sqrt{25}$ D、 $\sqrt{26}$

查看试题解析
2. 运算后结果正确的是（）

A、 $2 \sqrt{3} \div \frac{1}{2} = \sqrt{3}$ B、 $\sqrt[3]{4} = 2$ C、 $\sqrt{8} - 2 \sqrt{2} = 0$ D、 $\sqrt{2} \times \sqrt{6} = 3 \sqrt{2}$

查看试题解析
3. 关于x的方程ax²-3x+3＝0是一元二次方程，则a的取值范围是（）

A、a＞0 B、a≠0 C、a＝1 D、a≥0

查看试题解析
4. 一元二次方程x²-4x-6=0，经过配方可变形为（）

A、（x-2）²=10 B、（x-2）²=6 C、（x-2）²=2 D、（x+2）²=6

查看试题解析
5. 已知平行四边形 $A B C D$ 中， $∠ B = 4 ∠ A$ ，则 $∠ C$ 等于（　　）

A、 $144 °$ B、 $72 °$ C、 $54 °$ D、 $36 °$

查看试题解析
6. 如果将一组数据中的每个数都减去2022，那么所得的一组新数据（）

A、平均数不变 B、中位数不变 C、众数不变 D、方差不变

查看试题解析
7. 小红同学对数据32，41，37，37，4■进行统计分析，发现“4■”的个位数字被墨水涂污看不到了，则下列统计量与被涂污数字无关的是（）

A、方差 B、平均数 C、众数 D、中位数

查看试题解析
8. 小红：我计算出一个多边形的内角和为 $2020 °$ ；老师：不对呀，你可能少加了一个角 $！$ 则小红少加的这个角的度数是（）

A、110° B、120° C、130° D、140°

查看试题解析
9. 如图，在 ▱ ABCD中，对角线AC，BD相交于点O，过点O的直线EF交AB于点E，交CD于点F，且 $B E = \frac{1}{3} A B$ ，若 $S_{▱ A B C D} = 16$ ，则阴影部分面积是（）

A、 $\frac{4}{3}$ B、 $\frac{8}{3}$ C、2 D、3

查看试题解析
10. 已知关于x的一元二次方程 $(p + 1) x^{2} + 2 q x + (p + 1) = 0$ （其中p，q为常数）有两个相等的实数根，则下列结论中，错误的是（）．

A、1可能是方程 $x^{2} + q x + p = 0$ 的根 B、 $- 1$ 可能是方程 $x^{2} + q x + p = 0$ 的根 C、0可能是方程 $x^{2} + q x + p = 0$ 的根 D、1和 $- 1$ 都是方程 $x^{2} + q x + p = 0$ 的根

查看试题解析

二、填空题（每空4分，共24分）

11. 已知 $y =$ $\sqrt{x - 2} + \sqrt{2 - x} - \frac{1}{2}$ ，则 $x^{2021} \cdot y^{2020} =$ .

查看试题解析
12. 已知 $x = - 1$ 是一元二次方程 $x^{2} + m x + 2 = 0$ 的一个解，则m的值为.

查看试题解析
13. 某药店一月份销售口罩500包，一至三月份共销售口罩1820包，设该店二、三月份销售口罩的月平均增长率为x，则可列方程.

查看试题解析
14. 当a＝1＋ $\sqrt{2}$ ，b＝ $\sqrt{3}$ 时，a²＋b²－2a＋1＝．

查看试题解析
15. 小明某学期的数学平时成绩80分，期中考试90分，期末考试88分，若计算学期总评成绩的方法如下：平时：期中：期末=2：3：5，则小明学期总评成绩是分.

查看试题解析
16. 如图，在 $▱ A B C D$ 中，E点是BD的中点，MN经过E点分别与AD、BC相交于点M、N．下列四个结论：

① $A M = C N$ ；② $B M = B C$ ；③A、C、E三点共线；④若 $M D = 2 A M$ ，则 $S_{△ M N C} = S_{△ B N E}$ ．其中正确的结论有．（写出所有正确结论的序号）

查看试题解析

三、解答题（共7题，共66分）

17. 计算：

(1)、 $(\sqrt{48} + \sqrt{20}) - (\sqrt{12} - \sqrt{5})$ ；

(2)、 $\sqrt{48} + \sqrt{3} - 2 \sqrt{\frac{1}{4}} \times \sqrt{30} + {(2 \sqrt{2} + \sqrt{3})}^{2}$ ；

查看试题解析
18. 解方程：

(1)、 $3 x + 6 = (x + 2)^{2}$ ；

(2)、 $x^{2} - 2 \sqrt{2} x - 2 = 0$

查看试题解析
19. 如图，在 $▱ A B C D$ 中， $∠ A B C$ 和 $∠ B C D$ 的角平分线 $B E$ 与 $C E$ 相交于点 $E$ ，且点 $E$ 恰好落在 $A D$ 上；

(1)、求证： $B E^{2} + C E^{2} = B C^{2}$

(2)、若 $A B = 2$ ，求 $▱ A B C D$ 的周长．

查看试题解析
20. 某校八年级举办“防溺水安全知识答题竞赛”，甲、乙两个班根据初赛成绩各选出5名选手组成甲班代表队（简称：甲队）和乙班代表队（简称：乙队）参加学校决赛，甲队5名选手的决赛成绩（单位：分）分别是：85，80，75，85，100；乙队5名选手的决赛成绩（单位：分）分别是：100，80，100，75，70．
现将有关成绩整理成如下表格：

平均数/分
中位数/分
众数/分
方差
甲队
$a$
85
$b$
$s_{甲}^{2}$
乙队
85
$c$
100
160

(1)、直接写出 $a$ ， $b$ ， $c$ 的值．

(2)、结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？

(3)、学校决定从甲队和乙队中选择成绩较为稳定的一个代表队参加省级竞赛，你认为选哪个代表队合适？

查看试题解析
21. 已知关于x的一元二次方程 $x^{2} - 4 m x + 3 m^{2} = 0$ ．

(1)、求证：该方程总有两个实数根；

(2)、方程的两个实数根 $x_{1} ， x_{2}$ 满足 $(x_{1} + 1) (x_{2} + 1) = 5$ ，求实数m的值．

查看试题解析
22. 如图，四边形ABCD为平行四边形，E为AD上的一点，连接EB并延长，使 $B F = B E$ ，连接EC并延长，使 $C G = C E$ ，连接FG，H为FG的中点，连接DH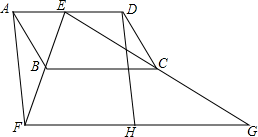

(1)、求证：四边形AFHD为平行四边形；

(2)、若 $C B = C E$ ， $∠ E B C = 75 °$ ， $∠ D C E = 10 °$ ，求 $∠ D A B$ 的度数.

查看试题解析
23. 某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，减少库存，商场决定采取适当的降价措施．经调查发现，每件衬衫每降价1元，商场平均每天可多售出2件．

(1)、求每件衬衫应降价多少元，能使商场每天盈利1200元；

(2)、小明的观点是：“商场每天的盈利可以达到1300元”，你同意小明的说法吗？若同意，请求出每件衬衫应降价多少元？若不同意，请说明理由．

查看试题解析

	平均数/分	中位数/分	众数/分	方差
甲队	$a$	85	$b$	$s_{甲}^{2}$
乙队	85	$c$	100	160