2023年浙教版数学八年级下学期高分速效复习8 平行四边形(进阶版)
试卷更新日期:2023-04-01 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 以下关于多边形内角和与外角和的表述,错误的是( )A、四边形的内角和与外角和相等 B、如果一个四边形的一组对角互补,那么另一组对角也互补 C、六边形的内角和是外角和是2倍 D、如果一个多边形的每个内角是120°,那么它是十边形.2. 如图所示的方格纸上有一平行四边形ABCD,其顶点均在网格线的交点上,且E点在AD上.今大华在方格纸网格线的交点上任取一点F,发现△FBC的面积比△EBC的面积大.判断下列哪一个图形可表示大华所取F点的位置?( )
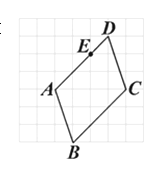 A、
A、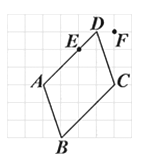 B、
B、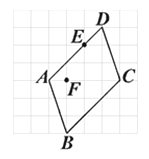 C、
C、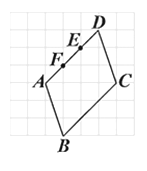 D、
D、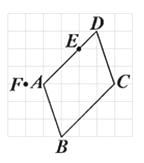 3. 在面积为的平行四边形ABCD中,分别过点A作直线BC的垂线AE,垂足为E,作直线CD的垂线AF,垂足为F.若AB= , BC= , 则CE+CF的值为( )A、 B、 C、或 D、或4. 如图,点O是 的对称中心, ,E、F是 边上的点,且 ;G、H是 边上的点,且 ,若 分别表示 和 的面积,则 与 之间的等量关系是( )
3. 在面积为的平行四边形ABCD中,分别过点A作直线BC的垂线AE,垂足为E,作直线CD的垂线AF,垂足为F.若AB= , BC= , 则CE+CF的值为( )A、 B、 C、或 D、或4. 如图,点O是 的对称中心, ,E、F是 边上的点,且 ;G、H是 边上的点,且 ,若 分别表示 和 的面积,则 与 之间的等量关系是( )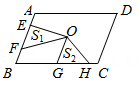 A、 B、 C、 D、5. 如图,在平面直角坐标系中,画关于点O成中心对称的图形时,由于紧张对称中心选错,画出的图形是 , 请你找出此时的对称中心是( )
A、 B、 C、 D、5. 如图,在平面直角坐标系中,画关于点O成中心对称的图形时,由于紧张对称中心选错,画出的图形是 , 请你找出此时的对称中心是( ) A、 B、 C、 D、6. 如图,已知▱OABC的顶点A,C分别在直线 和 上,O是坐标原点,则对角线OB长的最小值为( )
A、 B、 C、 D、6. 如图,已知▱OABC的顶点A,C分别在直线 和 上,O是坐标原点,则对角线OB长的最小值为( )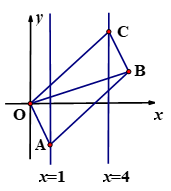 A、3 B、4 C、5 D、67. 如图,在四边形 中, , , ,E是 的中点.点P以每秒1个单位长度的速度从点A出发,沿 向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿 向点B运动.点P停止运动时,点Q也随之停止运动.若以点 为顶点的四边形是平行四边形,则点P运动的时间为( )
A、3 B、4 C、5 D、67. 如图,在四边形 中, , , ,E是 的中点.点P以每秒1个单位长度的速度从点A出发,沿 向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿 向点B运动.点P停止运动时,点Q也随之停止运动.若以点 为顶点的四边形是平行四边形,则点P运动的时间为( )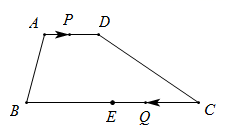 A、1 B、 C、2或 D、1或8. 根据图中所给的边长及角度,下列四边形中,一定可以判定为平行四边形的是( ).A、
A、1 B、 C、2或 D、1或8. 根据图中所给的边长及角度,下列四边形中,一定可以判定为平行四边形的是( ).A、 B、
B、 C、
C、 D、
D、 9. 如图,已知D、E分别是的边、的中点,是的中线,连接、、 , 若的面积为40,则阴影部分的面积为( )
9. 如图,已知D、E分别是的边、的中点,是的中线,连接、、 , 若的面积为40,则阴影部分的面积为( ) A、10 B、5 C、8 D、410. 已知 中, ,求证: ,下面写出运用反证法证明这个命题的四个步骤:
A、10 B、5 C、8 D、410. 已知 中, ,求证: ,下面写出运用反证法证明这个命题的四个步骤:①∴ ,这与三角形内角和为 矛盾②因此假设不成立.∴ ③假设在 中, ④由 ,得 ,即 .
这四个步骤正确的顺序应是( )
A、④③①② B、③④②① C、①②③④ D、③④①②二、填空题(每题3分,共18分)
-
11. 已知多边形的内角和与其某一个外角的度数总和为1350°,则这个多边形的边数为 , 其外角的度数为°,这个多边形一共有条对角线。12. 如图,在平行四边形ABCD中,AB=2AD,点E是DC的中点,作BF⊥AD,垂足F在线段AD上,连结EF,BE,则下列结论正确的是 .(将正确的结论的序号填在横线上)①EF=BE;②∠CBE= ∠ABC;③△ABF的面积等于△BEF的面积的2倍;④∠CEF=3∠DFE.
 13. 如图,直线垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点 , 于点B,于点D.若 , , 则阴影部分的面积之和为.
13. 如图,直线垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点 , 于点B,于点D.若 , , 则阴影部分的面积之和为. 14. 如图,在平面直角坐标系中,函数的图象分别交x轴,y轴于A,B两点,过点A的直线交y轴正半轴于点M,且 . 在平面直角坐标系内存在点C,使得以A,B,M,C为顶点的四边形是平行四边形,则点C的坐标为 .
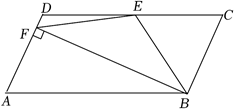
14. 如图,在平面直角坐标系中,函数的图象分别交x轴,y轴于A,B两点,过点A的直线交y轴正半轴于点M,且 . 在平面直角坐标系内存在点C,使得以A,B,M,C为顶点的四边形是平行四边形,则点C的坐标为 . 15. 如图,在▱ ABCD中,点E、F分别为AD、DC的中点,BF⊥CD,已知BF=8,EF=5,则▱ ABCD的周长为 .
15. 如图,在▱ ABCD中,点E、F分别为AD、DC的中点,BF⊥CD,已知BF=8,EF=5,则▱ ABCD的周长为 . 16. 在平面直角坐标系中,已知A、B、C、D四点的坐标依次为(0,0)、(6,0)、(8,6)、(2,6),若一次函数y=mx-6m的图象将四边形ABCD的面积分成1:3两部分,则m的值为 .
16. 在平面直角坐标系中,已知A、B、C、D四点的坐标依次为(0,0)、(6,0)、(8,6)、(2,6),若一次函数y=mx-6m的图象将四边形ABCD的面积分成1:3两部分,则m的值为 .三、作图题(共9分)
-
17. 如图,在6×6的方格纸中,每个小正方形的顶点称为格点,每个小正方形的边长均为1,A,B两点均在格点上.请按要求在图①,图②,图③中画图.

( 1 )在图①中,画等腰△ABC,使AB为腰,点C在格点上.
( 2 )在图②中,画面积为8的四边形ABCD,使其为中心对称图形,但不是轴对称图形,C,D两点均在格点上.
( 3 )在图③中,画△ABC,使∠ACB=90°,面积为5,点C在格点上.
四、解答题(共7题,共63分)
-
18. 用反证法证明:一个三角形中不能有两个角是直角.
已知: , , 是的三个内角.
求证: , , 中不能有两个角是直角.
19. 【知识链接】连结三角形两边中点的线段,叫做三角形的中位线.【动手操作】小明同学在探究证明中位线性质定理时,是沿着中位线将三角形剪开然后将它们无缝隙、无重叠的拼在一起构成平行四边形,从而得出:三角形中位线平行于第三边且等于第三边的一半.
【性质证明】小明为证明定理,他想利用三角形全等、平行四边形的性质来证明.请你帮他完成解题过程(要求:画出图形,根据图形写出已知、求证和证明过程).
20. 【发现与证明】如图,在四边形ABCD中,E、F、G、H是各边中点,对角线AC、BD相交于点O,I、J是AC、BD的中点,连接EF、EH、HG、GF、EI、GI、EJ、FJ、IJ、GJ、IH.
结论1:四边形EFGH是平行四边形;
结论2:四边形EJGI是平行四边形;
结论3:;
……
(1)、请选择其中一个结论,加以证明(只需证明一个结论). (2)、【探究与应用】(★温馨提示:以下问题可以直接使用上述结论)
(2)、【探究与应用】(★温馨提示:以下问题可以直接使用上述结论)
①如图1,在四边形ABCD中,F、H分别为边AB,DC的中点,连结HF.已知 , , 线段HF的取值范围是 ▲ .
②如图2,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,连接EG,FH交于点O,cm,cm, , 求.
21. 如图,在四边形中,为坐标原点,点 , 分别位于轴,轴正半轴上, , 为边的中点,为边上一点(不与点 , 重合),且 , , 分别与相交于点 , . (1)、求证:四边形是平行四边形;(2)、已知(4,8),当为等腰三角形时,求的长;(3)、当为中点时,连接并延长交于点 , 若四边形与△的面积差为4,请在横线上直接写出点的坐标.22. 在直角坐标系xOy中,四边形ABCD是矩形,点A在x轴上,点C在y轴的正半轴上,点B,D分别在第一,二象限,且AB=3,BC=4。
(1)、求证:四边形是平行四边形;(2)、已知(4,8),当为等腰三角形时,求的长;(3)、当为中点时,连接并延长交于点 , 若四边形与△的面积差为4,请在横线上直接写出点的坐标.22. 在直角坐标系xOy中,四边形ABCD是矩形,点A在x轴上,点C在y轴的正半轴上,点B,D分别在第一,二象限,且AB=3,BC=4。 (1)、如图1,延长CD交x轴负半轴于点E,若AC=AE。
(1)、如图1,延长CD交x轴负半轴于点E,若AC=AE。①求证:四边形ABDE为平行四边形。
②求点A的坐标。
(2)、如图2,F为AB上一点,G为AD的中点,若点G恰好落在y轴上,且CG平分∠DCF,求AF的长。(3)、如图3,x轴负半轴上的点P与点Q关于直线AD对称,且AP=AD,若OBCQ的面积为矩形ABCD面积的 ,则BQ的长可为(写出所有可能的答案)。23. 如图,在平面直角坐标系中,直线y=-x+8分别交两坐标轴于点A、B,直线CD与直线AB交于点C,与x轴交于点D.点C的横坐标为4,点D在线段OA上,且AD=7.
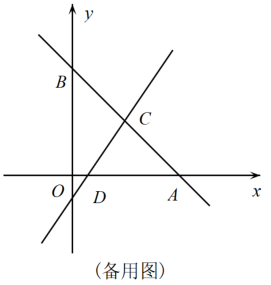
 (1)、C、D两点的坐标分别为;(2)、求直线CD的函数解析式;(3)、在坐标平面内是否存在这样的点F,使以A、C、D、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.24. 我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做等对角四边形.
(1)、C、D两点的坐标分别为;(2)、求直线CD的函数解析式;(3)、在坐标平面内是否存在这样的点F,使以A、C、D、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.24. 我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做等对角四边形.

 (1)、已知:如图1,四边形 是等对角四边形, , , ,则: °, °;(2)、图2、图3均为 的正方形网格,线段 , 的端点均在网点上.按要求在图2、图3中以 和 为边各画一个等对角四边形 .(要求:四边形 的顶点 在格点上,所画的两个四边形不全等)(3)、如图4,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,点 的坐标为 ,过点 作直线 垂直 轴,在直线 上是否存在一点 ,使四边形 为等对角四边形,如果存在,求出点 的坐标,如果不存在,请说明理由.
(1)、已知:如图1,四边形 是等对角四边形, , , ,则: °, °;(2)、图2、图3均为 的正方形网格,线段 , 的端点均在网点上.按要求在图2、图3中以 和 为边各画一个等对角四边形 .(要求:四边形 的顶点 在格点上,所画的两个四边形不全等)(3)、如图4,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,点 的坐标为 ,过点 作直线 垂直 轴,在直线 上是否存在一点 ,使四边形 为等对角四边形,如果存在,求出点 的坐标,如果不存在,请说明理由.
-