2023年浙教版数学八年级下学期高分速效复习7 平行四边形(基础版)
试卷更新日期:2023-04-01 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知一个多边形的内角和为 , 则这个多边形是( )A、八边形 B、七边形 C、六边形 D、五边形3. 五边形的外角和为( )A、360° B、540° C、720° D、900°4. 过一个多边形一个顶点的所有对角线,把这个多边形分成5个三角形,这个多边形是( )A、5 B、6 C、7 D、85. 如果过一个多边形的一个顶点的对角线有5条,则该多边形是( )A、九边形 B、八边形 C、七边形 D、六边形6. 如图,直线 , 则直线之间的距离是( )
2. 已知一个多边形的内角和为 , 则这个多边形是( )A、八边形 B、七边形 C、六边形 D、五边形3. 五边形的外角和为( )A、360° B、540° C、720° D、900°4. 过一个多边形一个顶点的所有对角线,把这个多边形分成5个三角形,这个多边形是( )A、5 B、6 C、7 D、85. 如果过一个多边形的一个顶点的对角线有5条,则该多边形是( )A、九边形 B、八边形 C、七边形 D、六边形6. 如图,直线 , 则直线之间的距离是( ) A、线段 B、线段的长度 C、线段 D、线段的长度7. 在中,若 , 则的度数是( )A、140° B、120° C、100° D、40°8. 下列不能判断一个四边形是平行四边形的是( )A、一组对边平行且相等的四边形 B、两组对边分别相等的四边形 C、对角线互相平分的四边形 D、一组对边相等,且另一组对边平行的四边形9. 刘师傅给客户加工一个平行四边形的零件,他要检查这个零件是否为平行四边形,用下列方法不能检查的是( )A、 , B、 , C、 , D、 ,10. 如图,在平行四边形中,对角线 , 相交于点O,E是AB的中点,连接 , 若cm,则的长为( )
A、线段 B、线段的长度 C、线段 D、线段的长度7. 在中,若 , 则的度数是( )A、140° B、120° C、100° D、40°8. 下列不能判断一个四边形是平行四边形的是( )A、一组对边平行且相等的四边形 B、两组对边分别相等的四边形 C、对角线互相平分的四边形 D、一组对边相等,且另一组对边平行的四边形9. 刘师傅给客户加工一个平行四边形的零件,他要检查这个零件是否为平行四边形,用下列方法不能检查的是( )A、 , B、 , C、 , D、 ,10. 如图,在平行四边形中,对角线 , 相交于点O,E是AB的中点,连接 , 若cm,则的长为( ) A、3cm B、6cm C、9cm D、12cm
A、3cm B、6cm C、9cm D、12cm二、填空题(每空4分,共24分)
-
11. 用反证法证明:在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等,证明时,可以先假设: .12. 如图,▱ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E,若△CDE的周长为10,则平行四边形ABCD的周长是
 13. 如图, , , , 分别是四边形边 , , , 的中点,若 , 则四边形的周长为 .
13. 如图, , , , 分别是四边形边 , , , 的中点,若 , 则四边形的周长为 . 14. 在平行四边形中,以A为圆心,长为半径画弧,交于F,再分别以B、F为圆心,大于的长为半径画弧,两弧相交于点G,若 , , 则的长为 .
14. 在平行四边形中,以A为圆心,长为半径画弧,交于F,再分别以B、F为圆心,大于的长为半径画弧,两弧相交于点G,若 , , 则的长为 . 15. 如图,把含45°,30°角的两块直角三角板放置在同一平面内,若AB//CD,AB=CD= , 则以A,B,C,D为顶点的四边形的面积是.
15. 如图,把含45°,30°角的两块直角三角板放置在同一平面内,若AB//CD,AB=CD= , 则以A,B,C,D为顶点的四边形的面积是. 16. 如图,已知四边形ABCD的对角线AC与BD相交于点O, , 添加一个条件 , 使四边形ABCD为平行四边形(填一个即可).
16. 如图,已知四边形ABCD的对角线AC与BD相交于点O, , 添加一个条件 , 使四边形ABCD为平行四边形(填一个即可).
三、作图题
-
17. 如图,已知△ABC的三个顶点的坐标分别为A(-3,0),B(-5,3),C(-1,1).

( 1 )画出△ABC关于原点O成中心对称的图形;
( 2 )P(a,b)是△ABC的AC边上一点,将△ABC平移后点P的对称点 , 请画出平移后的;
( 3 )若和关于某一点成中心对称,则对称中心的坐标为 .
四、解答题(共7题,共58分)
-
18. 用反证法证明:一个三角形中不能有两个直角。19. 若一个多边形的内角和的比它的外角和多 , 那么这个多边形的边数是多少?20. 如图,CD是△ABC的中线,E为CD上一点,连接AE并延长至点F,使 ,连接BF,CF,若CF∥AB.求证:四边形DBFC是平行四边形.
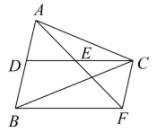 21. 如图,中,点 , 分别是边 , 的中点,过点作交的延长线于点 , 连结 .
21. 如图,中,点 , 分别是边 , 的中点,过点作交的延长线于点 , 连结 . (1)、求证:四边形是平行四边形.(2)、当时,若 , , 求的长.22. 如图,在平行四边形中,点E,F分别是边 , 的中点.
(1)、求证:四边形是平行四边形.(2)、当时,若 , , 求的长.22. 如图,在平行四边形中,点E,F分别是边 , 的中点. (1)、求证:;(2)、若四边形的周长为10, , , 求平行四边形的周长.
(1)、求证:;(2)、若四边形的周长为10, , , 求平行四边形的周长.
-

