2023年浙教版数学八年级下学期高分速效复习6 数据分析初步（进阶版）

试卷更新日期：2023-04-01 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 将一组数据的每一个数都减去30，所得新的一组数据的平均数是1，则原来那组数据的平均数为（）

A、31 B、30 C、1 D、29

查看试题解析
2. 一家公司打算招聘一名翻译对甲、乙、丙三名应试者进行了听、说、读、写的英语水平测试，他们各项成绩（百分制）如下表所示：
应试者
听
说
读
写
甲
73
80
82
83
乙
85
78
85
73
丙
80
82
80
80
如果这家公司想招一名笔译能力较强的翻译，听、说、读、写成绩按照2：1：3：4的比确定，从他们的平均成绩（百分制）看，应该录取（）

A、甲 B、乙 C、丙 D、不确定

查看试题解析
3. 疫情无情人有情，爱心捐款传真情．新冠肺炎疫情发生后，某班学生积极参加献爱心活动，该班 $40$ 名学生的捐款统计情况如下表，关于捐款金额，下列说法错误的是（）
金额/元
10
20
30
50
100
人数
2
18
10
8
2

A、平均数为 $32$ 元 B、众数为 $20$ 元 C、中位数为 $20$ 元 D、极差为 $90$ 元

查看试题解析
4. 已知一组数据1，2，3，4，5，a，b的平均数是4，若该组数据的中位数小于4，则a的值可能是（）

A、7 B、8 C、9 D、10

查看试题解析
5. 一组从小到大排列的数据：x，3，4，4，5（x为正整数），唯一的众数是4，则该组数据的平均数是（）

A、3.6 B、3.2或3.8 C、3.4或3.6 D、3.2或3.6

查看试题解析
6. 若样本x₁+1，x₂+1，…，x_n+1的平均数为10，方差为2，则对于样本x₁+2，x₂+2，…，x_n+2，下列结论正确的是（）

A、平均数为10，方差为2 B、平均数为11，方差为3 C、平均数为11，方差为2 D、平均数为12，方差为4

查看试题解析
7. 教练将某射击运动员50次的射击成绩录入电脑，计算得到这50个数据的平均数是7.5，方差是1.64．后来教练核查时发现其中有2个数据录入有误，一个错录为6环，实际成绩应是8环；另一个错录为9环，实际成绩应是7环．教练将错录的2个数据进行了更正，更正后实际成绩的平均数是 $\bar{x}$ ，方差是 $s^{2}$ ，则（）

A、 $\bar{x} < 7.5$ ， $s^{2} = 1.64$ B、 $\bar{x} = 7.5$ ， $s^{2} > 1.64$ C、 $\bar{x} > 7.5$ ， $s^{2} < 1.64$ D、 $\bar{x} = 7.5$ ， $s^{2} < 1.64$

查看试题解析
8. 一组数据为7，9，9，11，若添加一个数据9，则发生变化的统计量是（）

A、方差 B、众数 C、中位数 D、平均数

查看试题解析
9. 若一组数据x₁ ， x₂ ， …x_n的平均数为17，方差为2，则另一组数据x₁+1，x₂+1，…，x_n+1的平均数、方差分别为（）

A、17，2 B、18，2 C、17，3 D、18，3

查看试题解析
10. 某校六一活动中，10位评委给某个节目的评分各不相同，去掉1个最高分和1个最低分，剩下的8个评分与原始的10个评分相比（）

A、平均数一定不发生变化 B、中位数一定不发生变化 C、方差一定不发生变化 D、众数一定不发生变化

查看试题解析

二、填空题（每空4分，共24分）

11. 已知：一组自然数1，2，3…k，去掉其中一个数后剩下的数的平均数为16，则去掉的数是．

查看试题解析
12. 已知一组正整数2，m，3，n，3，2的众数是2，且m，n是一元二次方程x²﹣7x+k＝0的两个根，则这组数据的中位数是．

查看试题解析
13. 寒假期间，滑雪冬令营的同学们都参加了“单板滑雪”这个项目的40次的训练测试，每次测试成绩分别为5分，4分，3分，2分，1分五档，甲、乙两位同学在这个项目的测试成绩统计结果如图所示：
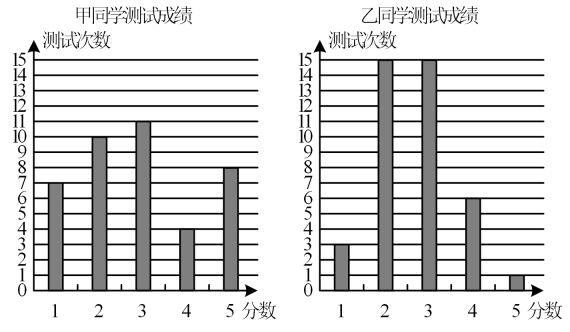
结合图中数据，请你从平均数、众数、中位数、方差中选择一方面评论一下两位同学的滑雪成绩．

查看试题解析
14. 2022年5月30日是第六个全国科技工作者日，主题为“创新争先，自立自强”．为了庆祝第六个全国科技工作者日，某学校准备举办科技知识竞赛活动， $A$ 班需要从甲，乙两位同学中选拔一位同学参加学校举办的此次活动，甲、乙两位同学的5次选拔成绩如统计图所示，两位同学的平均成绩相等，从他们的稳定性考虑，应该选择的同学是．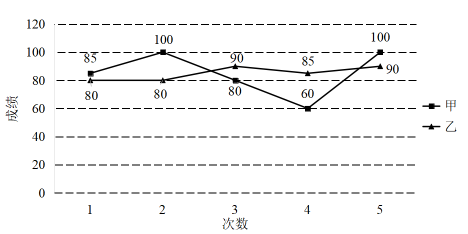

查看试题解析
15. 小聪同学在计算一组数据1、3、4、5、x的方差时，写出的计算过程是： $S^{2} = \frac{1}{5} [(1 - 4)^{2} + (3 - 4)^{2} + (4 - 4)^{2} + (5 - 4)^{2} + (x - 4)^{2}] = 4$ ，如果他的计算是正确的，你认为这组数据中的x为．

查看试题解析
16. 某班有50人，一次数学测试后，老师对测试成绩进行了统计．由于小明没有参加此次集体测试，因此计算其他49人的平均分为92分，方差 $S_{1}^{2} = 5$ ．后来小明进行了补测，成绩是92分，则该班50人的数学测试成绩的方差 $S_{2}^{2} =$ ．

查看试题解析

三、解答题（共6题，共66分）

17. 2021年12月，中共玉溪市红塔区委办公室、玉溪市红塔区人民政府办公室印发《玉溪市红塔区进一步减轻义务教育阶段学生作业负担和校外培训负担的实施方案》，文件明确要求，建立作业统筹管理机制，科学合理布置作业，严控作业总量和时长，切实减轻学生过重课业负担，初中学生每天书面作业平均完成时间不超过90分钟，周末、寒暑假、法定节假日也控制书面作业时间，某校为了解在“双减”政策下九年级学生每天书面作业完成时间（单位：分钟）的落实情况，在九年级学生中随机抽取部分学生进行了一次问卷调查，并将调查结果统计如下表：
每天书面完成时间t/分钟
$30 < t \leq 50$
$50 < t \leq 70$
$70 < t \leq 90$
$90 < t \leq 110$
$110 < t \leq 130$
人数
2
10
15
17
6

(1)、直接写出本次调查的样本容量，中位数所在的范围及平均数（计算平均数时，可用各组的组中值代表各组的实际数据）；

(2)、直接写出抽取的学生每天书面作业完成时间超过90分钟的人数，估计该校九年级学生每天书面作业平均完成时间是否符“双减”政策的要求，并说明理由．

查看试题解析
18. 用水问题一直是台州人民关注的热点问题，为此，小明随机抽取自己家中一年5个月的月用水量（单位：吨），并对每个月的月平均气温（单位：℃）进行了统计，得到下列统计图

(1)、小明家这5个月的月平均用水量为吨；

(2)、下列推断：①当地当年月平均气温的众数是26℃；
②当地当年月平均气温的中位数为17.5℃；
③小明家这5个月的月用水量随着月平均气温的变化而变化，温度越高，月用水最越大．所有合理推断的序号是；

(3)、如果用小明家5月、7月、9月这三个月的月平均用水量估计当年的用水总量，你认为是否合理？并说明理由．

查看试题解析
19. 甲乙两人在相同的条件下各射击10次，每次射击的成绩情况如图所示．（方差的计算公式：s²＝ $\frac{1}{n}$ [（x₁﹣ $\bar{x}$ ）²+（x₂﹣ $\bar{x}$ ）²+……+（x_n﹣ $\bar{x}$ ）²]．）

(1)、请你填写甲的相关数据：

平均数

众数

方差

甲

(2)、如果甲第11次射击的成绩是8环，则甲得分中的三个统计量，即平均数、众数、方差发生哪些变化？

(3)、根据甲、乙10次射击的成绩，如果教练选择甲参加射击比赛，教练的理由是什么？如果教练选择乙参加射击比赛，教练的理由又是什么？

查看试题解析

20. 某中学为加强学生的劳动教育，需要制定学生每周劳动时间（单位：小时）的合格标准，为此随机调查了100名学生目前每周劳动时间，获得数据并整理成表格．

学生目前每周劳动时间统计表

每周劳动时间 x（小时）	$0.5 \leq x < 1.5$	$1.5 \leq x < 2.5$	$2.5 \leq x < 3.5$	$3.5 \leq x < 4.5$	$4.5 \leq x < 5.5$
组中值	1	2	3	4	5
人数（人）	21	30	19	18	12

(1)、画扇形图描述数据时，1.5≤x＜2.5这组数据对应的扇形圆心角是多少度？

(2)、估计该校学生目前每周劳动时间的平均数；

(3)、请你为该校制定一个学生每周劳动时间的合格标准（时间取整数小时），并用统计量说明其合理性．

查看试题解析

21. 甲、乙两校各组织300名学生参加联赛，为了解两校联赛成绩情况，在两校随机抽取部分学生的联赛成绩，两校抽取的人数相等，结果如下（数据包括左端点不包括右端点）．

甲校抽取的学生联赛成绩频数分布表

分组	频数
30≤x<40	1
40≤x<50	2
50≤x<60	5
60≤x<70	9
70≤x<80	11
80≤x<90	15
90≤x<10	7

(1)、若小明是乙校的学生，他的成绩是75分，请结合数据分析小明的成绩；

(2)、若甲校中一位同学的成绩不纳入计算后，甲校的平均成绩提高了，这位同学的成绩不可能在哪些分数段？

(3)、请用适当的统计量从两个不同角度分析哪所学校的联赛成绩整体较好？

查看试题解析

22. 重庆市2022年体育中考将在3月底4月初进行，近日，某中学初三年级组织了一次体育中考模拟测试．现从该校初三年级男女生中各抽取10名同学的成绩进行统计分析（成绩得分用x表示，共分成四组：A：30≤x＜35，B：35≤x＜40，C：40≤x＜45，D：45≤x≤50），绘制了如下的图表，请根据图中的信．息解答下列问题，
10名男生的成绩是：32，34，38，43，44，45，47，48，50，50
10名女生的成绩在C组中的数据是：43，44，44
男生、女生抽取学生测试成绩统计表
年级
平均数
中位数
众数
D组占比
男生
43.1
44.5
b
c
女生
43.1
a
44
40%

(1)、直接写出上表中a，b，c的值；

(2)、根据以上数据，你认为该校初三年级男生和女生谁的体育成绩更好？请说明理由；（写出一条理由即可）

(3)、若该校初三年级共有400人参加了此次测试，估计参加此次测试成绩优秀（45≤x≤50）的学生共有多少人？

查看试题解析

每天书面完成时间t/分钟	$30 < t \leq 50$	$50 < t \leq 70$	$70 < t \leq 90$	$90 < t \leq 110$	$110 < t \leq 130$
人数	2	10	15	17	6

年级	平均数	中位数	众数	D组占比
男生	43.1	44.5	b	c
女生	43.1	a	44	40%

应试者	听	说	读	写
甲	73	80	82	83
乙	85	78	85	73
丙	80	82	80	80

金额/元	10	20	30	50	100
人数	2	18	10	8	2

	平均数	众数	方差
甲