福建省漳州市2023届高三毕业班数学第三次质量检测试卷

试卷更新日期：2023-03-31 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x^{2} - 2 x - 8 < 0}$ ， $B = {x | | x - 3 | < 2}$ ，则 $A \cup B =$ （）

A、 $(- 2 ， 5)$ B、 $(- 2 ， 4)$ C、 $(1 ， 4)$ D、 $(- 2 ， 1)$

查看试题解析
2. 已知复数 $\bar{z}$ 为复数 $z$ 的共轭复数，且满足 $z = {\bar{z}}^{2}$ ， $z$ 在复平面内对应的点在第二象限，则 $| z | =$ （）

A、 $\sqrt{3}$ B、 $\sqrt{2}$ C、1 D、 $\frac{1}{2}$

查看试题解析
3. 已知数列 ${a_{n}}$ 为递减的等比数列， $n \in N^{*}$ ，且 $a_{2} a_{7} = 32$ ， $a_{3} + a_{6} = 18$ ，则 ${a_{n}}$ 的公比为（）

A、 $\frac{1}{2}$ B、 ${(\frac{1}{2})}^{\frac{3}{5}}$ C、 $2^{\frac{3}{5}}$ D、 $2$

查看试题解析
4. 英国物理学家和数学家牛顿曾提出物体在常温环境下温度变化的冷却模型.如果物体的初始温度是 $θ_{1}$ ，环境温度是 $θ_{0}$ ，则经过 $t m i n$ 物体的温度 $θ$ 将满足 $θ = θ_{0} + (θ_{1} - θ_{0}) e^{- k t}$ ，其中 $k$ 是一个随着物体与空气的接触情况而定的正常数.现有 $90 {}_{∘}C$ 的物体，若放在 $10 {}_{∘}C$ 的空气中冷却，经过 $10 m i n$ 物体的温度为 $50 {}_{∘}C$ ，则若使物体的温度为 $20 {}_{∘}C$ ，需要冷却（）

A、 $17.5 m i n$ B、 $25.5 m i n$ C、 $30 m i n$ D、 $32.5 m i n$

查看试题解析
5. 已知 $s i n (α + \frac{π}{6}) = \frac{\sqrt{2}}{4}$ ，则 $s i n (2 α + \frac{5 π}{6}) =$ （）

A、 $- \frac{3}{4}$ B、 $\frac{3}{4}$ C、 $- \frac{3 \sqrt{2}}{4}$ D、 $\frac{3 \sqrt{2}}{4}$

查看试题解析
6. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左焦点为 $F_{1}$ ，直线 $y = k x (k > 0)$ 与双曲线 $C$ 交于 $P ， Q$ 两点，且 $∠ P F_{1} Q = \frac{2 π}{3}$ ， $\vec{P F_{1}} \cdot \vec{F_{1} Q} = 4$ ，则当 $\frac{1}{2} a^{2} + \frac{b^{2}}{a^{2}}$ 取得最小值时，双曲线 $C$ 的离心率为（）

A、3 B、 $\sqrt{3}$ C、2 D、 $\sqrt{2}$

查看试题解析
7. 已知正三棱锥 $P - A B C$ 的侧面与底面所成的二面角为 $\frac{π}{3}$ ，侧棱 $P A = \frac{\sqrt{21}}{2}$ ，则该正三棱锥的外接球的表面积为（）

A、 $\frac{7 π}{4}$ B、 $\frac{7 π}{12}$ C、 $\frac{49 π}{4}$ D、 $\frac{49 π}{12}$

查看试题解析
8. 已知函数 $f (x) = 2 x + l n x + 1 - a$ 和函数 $g (x) = x - \frac{a}{e^{2 x}}$ ，具有相同的零点 $x_{0}$ ，则 $e^{2 x_{0}} l n x_{0}^{2}$ 的值为（）

A、2 B、 $- e$ C、-4 D、 $e^{2}$

查看试题解析

二、多选题

9. 已知附件某地区甲、乙两所高中学校的六次联合模拟考试的数学平均分数（满分 $150$ 分）的统计如图所示，则（）

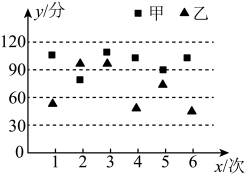A、甲校的平均分均高于乙校的平均分 B、甲校六次平均分的方差小于乙校六次平均分的方差 C、甲校六次平均分第 $25$ 百分位数小于乙校六次平均分的第 $75$ 百分位数 D、甲校的平均分极差小于乙校的平均分极差

查看试题解析
10. 在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $P$ 为线段 $B_{1} C$ 上的动点，则（）

A、 $A P / /$ 平面 $A_{1} C_{1} D$ B、 $B_{1} D ⊥$ 平面 $A C D_{1}$ C、三棱锥 $C_{1} - P D A_{1}$ 的体积为定值 D、直线 $A P$ 与 $A_{1} D$ 所成角的取值范围是 $[\frac{π}{6} ， \frac{π}{2}]$

查看试题解析
11. 已知函数 $f (x) = s i n \frac{ω x}{2} c o s \frac{ω x}{2} + c o s^{2} \frac{ω x}{2} - \frac{1}{2} (ω > 0)$ 在 $[0 ， π]$ 上有且仅有 $4$ 条对称轴；则（）

A、 $ω \in [\frac{13}{4} ， \frac{17}{4})$ B、 $π$ 可能是 $f (x)$ 的最小正周期 C、函数 $f (x)$ 在 $(- \frac{π}{16} ， \frac{π}{16})$ 上单调递增 D、函数 $f (x)$ 在 $(0 ， π)$ 上可能有 $3$ 个或 $4$ 个零点

查看试题解析
12. 已知数列 ${a_{n}}$ ， $a_{2} = \frac{1}{2}$ ，且满足 $a_{n + 1} a_{n}^{2} = a_{n} - a_{n + 1}$ ， $n \in N^{*}$ ，则（）

A、 $a_{4} - a_{1} = \frac{19}{29}$ B、 $a_{n}$ 的最大值为 $1$ C、 $a_{n + 1} \geq \frac{1}{n + 1}$ D、 $\sqrt{a_{1}} + \sqrt{a_{2}} + \sqrt{a_{3}} + \cdot \cdot \cdot + \sqrt{a_{35}} > 10$

查看试题解析

三、填空题

13. 已知函数 $f (x)$ 是定义在 $[- 2 ， 2]$ 上的奇函数，且 $f (x) = {\begin{array}{l} x^{2} - x ， 0 < x \leq 1 \\ x - 1 ， 1 < x \leq 2 \end{array}$ ，则 $f (- \frac{3}{2}) + f (\frac{1}{2}) + f (0) =$ .

查看试题解析
14. ${(x^{2} - 2 y + 2)}^{5}$ 的展开式中 $x^{4} y^{2}$ 项的系数为.

查看试题解析
15. 已知 $△ A B C$ ，点D满足 $\vec{B C} = \frac{3}{4} \vec{B D}$ ，点E为线段CD上异于C，D的动点，若 $\vec{A E} = λ \vec{A B} + μ \vec{A C}$ ，则 $λ^{2} + μ^{2}$ 的取值范围是.

查看试题解析
16. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的长轴长为 $4$ ，离心率为 $\frac{\sqrt{3}}{2}$ ， $P ， Q$ 为 $C$ 上的两个动点，且直线 $O P$ 与 $O Q$ 斜率之积为 $- \frac{1}{4}$ （ $O$ 为坐标原点），则椭圆 $C$ 的短轴长为， ${| O P |}^{2} + {| O Q |}^{2} =$ .

查看试题解析

四、解答题

17. 已知 $S_{n}$ 为等差数列 ${a_{n}}$ 的前 $n$ 项和， $n \in N^{*}$ ， $3 a_{2} - a_{5} = 6$ ， $S_{6} = 54$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $\frac{(n + 3) b_{n}}{2} = \frac{1}{a_{n}}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
18. 如图，平面四边形 $A B C D$ 内接于圆O，内角 $B > D$ ，对角线AC的长为7，圆 $O$ 的半径为 $\frac{7 \sqrt{3}}{3}$ .

(1)、若 $B C = 5$ ， $A D = C D$ ，求四边形 $A B C D$ 的面积；

(2)、求 $△ A B C$ 周长的最大值.

查看试题解析
19. 如图，在直四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，底面 $A B C D$ 是边长为 $2$ 的菱形， $D D_{1} = 3$ ， $∠ A B C = \frac{2 π}{3}$ ， $G$ 为棱 $D D_{1}$ 上一点， $D G = 2$ ，过 $A ， G ， C_{1}$ 三点的平面 $α$ 交 $B B_{1}$ 于点 $E$ .

(1)、求点 $D$ 到平面 $B C_{1} G$ 的距离；

(2)、求平面 $A E C$ 与平面 $B E C$ 所成锐二面角的余弦值.

查看试题解析
20. $2022$ 年 $11$ 月 $17$ 日，由工业和信息化部、安徽省人民政府共同主办的第十七届“中国芯”集成电路产业大会在合肥成功举办．此次大会以“强芯固基以质为本”为主题，旨在培育壮大我国集成电路产业，夯实产业基础、营造良好产业生态. $2022$ 年，全国芯片研发单位相比 $2006$ 年增加 $194$ 家，提交芯片数量增加 $299$ 个，均增长超过 $6$ 倍.某芯片研发单位用在“ $A$ 芯片”上研发费用占本单位总研发费用的百分比 $y$ （ $%$ ）如表所示.
年份
$2016$
$2017$
$2018$
$2019$
$2020$
$2021$
$2022$
年份代码
$1$
$2$
$3$
$4$
$5$
$6$
$7$
$y$
$20 %$
$30 %$
$32 %$
$39 %$
$42 %$
$46 %$
$50 %$
附：相关数据： $\sum_{i = 1}^{7} y_{i} = 259$ ， $\sqrt{7} \approx 2.65$ ， $\sqrt{\sum_{i = 1}^{7} {(y_{i} - \bar{y})}^{2}} \approx 25.34$ ， $\sum_{i = 1}^{7} (t_{i} - \bar{t}) (y_{i} - \bar{y}) = 132$ .
相关计算公式：①相关系数 $r = \frac{\sum_{i = 1}^{n} (t_{i} - \bar{t}) (y_{i} - \bar{y})}{\sqrt{\sum_{i = 1}^{n} {(t_{i} - \bar{t})}^{2} \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}$ ；
在回归直线方程 $\hat{y} = \hat{b} x + \hat{a}$ 中， $\hat{b} = \frac{\sum_{i = 1}^{n} (t_{i} - \bar{t}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(t_{i} - \bar{t})}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{t}$ .

(1)、根据表中的数据，作出相应的折线图；并结合相关数据，计算相关系数 $r$ ，并推断 $y$ 与 $t$ 线性相关程度；（已知： $0.8 \leq | r | \leq 1$ ，则认为 $y$ 与 $t$ 线性相关很强； $0.3 \leq | r | < 0.8$ ，则认为 $y$ 与 $t$ 线性相关一般； $| r | < 0.3$ ，则认为 $y$ 与 $t$ 线性相关较弱）

(2)、求出 $y$ 与 $t$ 的回归直线方程（保留一位小数）；

(3)、请判断，若 $2024$ 年用在“ $A$ 芯片”上研发费用不低于 $295$ 万元，则该单位 $2024$ 年芯片研发的总费用预算为 $500$ 万元是否符合研发要求?

查看试题解析
21. 已知函数 $f (x) = a x - e^{x} + \frac{l n x}{a} (a > 0)$ .

(1)、证明：当 $a = 1$ 时，函数 $f (x)$ 在区间 $(0 ， + ∞)$ 上不是单调函数；

(2)、证明：当 $a \in (0 ， e)$ 时， $f (x) < 0$ 对任意的 $x \in (0 ， 1)$ 恒成立.

查看试题解析
22. 已知椭圆 $C$ 的中心为坐标原点 $O$ ，对称轴为 $x$ 轴、 $y$ 轴，且点 $(\sqrt{3} ， 2 \sqrt{2})$ 和点 $(\sqrt{6} ， 2)$ 在椭圆 $C$ 上，椭圆的左顶点与抛物线 $Γ ： y^{2} = 2 p x (p > 0)$ 的焦点 $F$ 的距离为 $4$ .

(1)、求椭圆 $C$ 和抛物线 $Γ$ 的方程；

(2)、直线 $l ： y = k x + m (k \neq 0)$ 与抛物线 $Γ$ 变于 $P ， Q$ 两点，与椭圆 $C$ 交于 $M ， N$ 两点.
（ⅰ）若 $m = k$ ，抛物线 $Γ$ 在点 $P ， Q$ 处的切线交于点 $S$ ，求证： $| P F | \cdot {| S Q |}^{2} = | Q F | \cdot {| S P |}^{2}$ ；
（ⅱ）若 $m = - 2 k$ ，是否存在定点 $T (x_{0} ， 0)$ ，使得直线 $M T ， N T$ 的倾斜角互补?若存在，求出 $x_{0}$ 的值；若不存在，请说明理由.

查看试题解析

年份	$2016$	$2017$	$2018$	$2019$	$2020$	$2021$	$2022$
年份代码	$1$	$2$	$3$	$4$	$5$	$6$	$7$
$y$	$20 %$	$30 %$	$32 %$	$39 %$	$42 %$	$46 %$	$50 %$