福建省厦门市2023届高三下学期数学第二次质量检测试卷
试卷更新日期:2023-03-31 类型:高考模拟
一、单选题
-
1. 复数z1 , z2在复平面内对应的点分别为(1,2),(0,-1),则z1z2=( )A、1+i B、2-i C、-2i D、-2-i2. 的展开式中x2y3项的系数等于80,则实数a=( )A、2 B、±2 C、 D、±3. 不等式()恒成立的一个充分不必要条件是( )A、a≥1 B、a>1 C、 D、a>24. 西施壶是紫砂壶器众多款式中最经典的壶型之一,是一款非常实用的泡茶工具(如图1).西施壶的壶身可近似看成一个球体截去上下两个相同的球缺的几何体.球缺的体积(R为球缺所在球的半径,h为球缺的高).若一个西施壶的壶身高为8cm,壶口直径为6cm(如图2),则该壶壶身的容积约为(不考虑壶壁厚度,π取3.14)( )
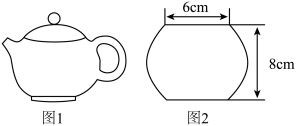 A、494mL B、506mL C、509mL D、516mL5. 厦门山海健康步道云海线全长约23公里,起于东渡邮轮广场,终于观音山沙滩,沿线申联贸鸟湖、狐尾山、仙岳山、园山、薛岭山、虎头山、金山、湖边水库、五缘湾、虎仔山、观音山等“八山三水”.市民甲计划从“八山三水”这11个景点中随机选取相邻的3个游览,则选取的景点中有“水”的概率为( )A、 B、 C、 D、6. 如图,( )
A、494mL B、506mL C、509mL D、516mL5. 厦门山海健康步道云海线全长约23公里,起于东渡邮轮广场,终于观音山沙滩,沿线申联贸鸟湖、狐尾山、仙岳山、园山、薛岭山、虎头山、金山、湖边水库、五缘湾、虎仔山、观音山等“八山三水”.市民甲计划从“八山三水”这11个景点中随机选取相邻的3个游览,则选取的景点中有“水”的概率为( )A、 B、 C、 D、6. 如图,( )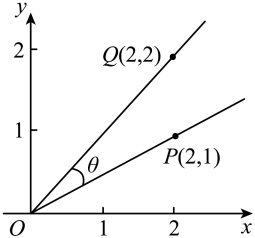 A、 B、 C、 D、7. 圆为锐角的外接圆, , 点在圆上,则的取值范围为( )A、 B、 C、 D、8. 已知 , , , 则( )A、c>b>a B、a>b>c C、c>a>b D、b>a>c
A、 B、 C、 D、7. 圆为锐角的外接圆, , 点在圆上,则的取值范围为( )A、 B、 C、 D、8. 已知 , , , 则( )A、c>b>a B、a>b>c C、c>a>b D、b>a>c二、多选题
-
9. 李明每天7:00从家里出发去学校,有时坐公交车,有时骑自行车.他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30分钟,样本方差为36;自行车平均用时34分钟,样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布,则( )A、P(X>32)>P(Y>32) B、P(X≤36)=P(Y≤36) C、李明计划7:34前到校,应选择坐公交车 D、李明计划7:40前到校,应选择骑自行车10. 函数f(x)=b(x-a)2(x-b)的图象可以是( )A、
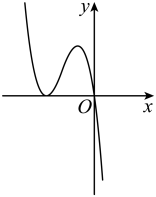 B、
B、 C、
C、 D、
D、 11. 如图的六面体中,CA=CB=CD=1,AB=BD=AD=AE=BE=DE= , 则( )
11. 如图的六面体中,CA=CB=CD=1,AB=BD=AD=AE=BE=DE= , 则( )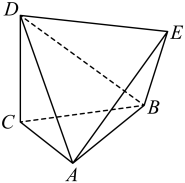 A、CD⊥平面ABC B、AC与BE所成角的大小为 C、 D、该六面体外接球的表面积为3π12. 定义在R上的函数满足 , 函数的图象关于对称,则( )A、的图象关于对称 B、4是的一个周期 C、 D、
A、CD⊥平面ABC B、AC与BE所成角的大小为 C、 D、该六面体外接球的表面积为3π12. 定义在R上的函数满足 , 函数的图象关于对称,则( )A、的图象关于对称 B、4是的一个周期 C、 D、三、填空题
-
13. 将函数的图象向左平移个单位长度.得到函数g(x)的图象,若g(x)是奇函数,则φ= .14. 写出与直线 和圆都相切的一个圆的方程 .15. 数列满足 , 若 , , 则= .16. 不与x轴重合的直线l过点N( , 0)(xN≠0),双曲线C:(a>0,b>0)上存在两点A、B关于l对称,AB中点M的横坐标为 . 若 , 则C的离心率为 .
四、解答题
-
17. 的内角的对边分别为 , 已知 .(1)、求B;(2)、A的角平分线与C的角平分线相交于点D, , , 求和 .18. 如图,在直四棱柱ABCD-A1B1C1D1中,AB⊥AD,A1D⊥BD1 .
 (1)、证明:四边形ADD1A1为正方形;(2)、若直线BD1与平面ABCD所成角的正弦值为 , CD=2AB,求平面ABD1与平面BCD1的夹角的大小.19. 记等差数列的公差为 , 前项和为;等比数列的公比为 , 前项和为 , 已知 , , .(1)、求和;(2)、若 , , 求的前项和.20. 移动物联网广泛应用于生产制造、公共服务、个人消费等领域.截至2022年底,我国移动物联网连接数达18.45亿户,成为全球主要经济体中首个实现“物超人”的国家.右图是2018-2022年移动物联网连接数W与年份代码t的散点图,其中年份2018-2022对应的t分别为1~5.
(1)、证明:四边形ADD1A1为正方形;(2)、若直线BD1与平面ABCD所成角的正弦值为 , CD=2AB,求平面ABD1与平面BCD1的夹角的大小.19. 记等差数列的公差为 , 前项和为;等比数列的公比为 , 前项和为 , 已知 , , .(1)、求和;(2)、若 , , 求的前项和.20. 移动物联网广泛应用于生产制造、公共服务、个人消费等领域.截至2022年底,我国移动物联网连接数达18.45亿户,成为全球主要经济体中首个实现“物超人”的国家.右图是2018-2022年移动物联网连接数W与年份代码t的散点图,其中年份2018-2022对应的t分别为1~5.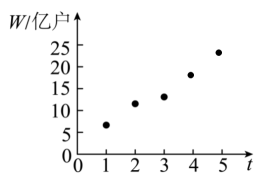
附:样本相关系数 , , , ,
(1)、根据散点图推断两个变量是否线性相关.计算样本相关系数(精确到0.01),并推断它们的相关程度;(2)、(i)假设变量x与变量Y的n对观测数据为(x1 , y1),(x2 , y2),…,(xn,yn),两个变量满足一元线性回归模型 (随机误差).请推导:当随机误差平方和Q=取得最小值时,参数b的最小二乘估计.(ii)令变量 , 则变量x与变量Y满足一元线性回归模型利用(i)中结论求y关于x的经验回归方程,并预测2024年移动物联网连接数.