福建省泉州市2023届高三数学质量监测试卷（三）

试卷更新日期：2023-03-31 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | - 5 < x < 2}$ ， $B = {x | | x | < 3}$ ，则 $A \cup B =$ （）

A、 $(- \infty ， 2)$ B、 $(- \infty ， 3)$ C、 $(- 3 ， 2)$ D、 $(- 5 ， 3)$

查看试题解析
2. 已知复数 $z$ 满足 $(1 - i) z = 4 i$ ，则 $z \cdot \bar{z} =$ （）

A、-8 B、0 C、8 D、 $8 i$

查看试题解析
3. 已知 $s i n α - \sqrt{2} c o s α = 0$ ，则 $c o s 2 α =$ （）

A、 $- \frac{1}{3}$ B、0 C、 $\frac{1}{3}$ D、 $\frac{\sqrt{2}}{3}$

查看试题解析
4. 某运动员每次射击击中目标的概率均相等，若三次射击中，至少有一次击中目标的概率为 $\frac{63}{64}$ ，则射击一次，击中目标的概率为（）

A、 $\frac{7}{8}$ B、 $\frac{3}{4}$ C、 $\frac{1}{4}$ D、 $\frac{1}{8}$

查看试题解析
5. 已知抛物线 $C$ 的焦点为 $F$ ，准线为 $l$ ，点 $A$ 在 $C$ 上，点 $B$ 在 $l$ 上．若 $| \vec{A F} | = | \vec{B F} | = 4$ ， $\vec{A F} \cdot (\vec{B F} + \vec{B A}) = 0$ ，则 $F$ 到 $l$ 的距离等于（）

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
6. 定义在 $R$ 上的偶函数 $f (x)$ 满足 $f (2 - x) + f (x) = 0$ ，且当 $x \in [0 ， 1)$ 时， $f (x) = \sqrt{x} - 1$ ，则曲线 $y = f (x)$ 在点 $(- \frac{9}{4} ， f (- \frac{9}{4}))$ 处的切线方程为（）

A、 $4 x - 4 y + 11 = 0$ B、 $4 x + 4 y + 11 = 0$ C、 $4 x - 4 y + 7 = 0$ D、 $4 x + 4 y + 7 = 0$

查看试题解析
7. 图1中，正方体 $A B C D - E F G H$ 的每条棱与正八面体 $M P Q R S N$ （八个面均为正三角形）的条棱垂直且互相平分．将该正方体的顶点与正八面体的顶点连结，得到图2的十二面体，该十二面体能独立密铺三维空间．若 $A B = 1$ ，则点M到直线 $R G$ 的距离等于（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{6}}{2}$ D、 $\frac{\sqrt{7}}{2}$

查看试题解析
8. 已知平面向量 $\vec{a}$ 、 $\vec{b}$ 、 $\vec{c}$ 满足 $| \vec{a} | = 1$ ， $\vec{b} \cdot \vec{c} = 0$ ， $\vec{a} \cdot \vec{b} = 1$ ， $\vec{a} \cdot \vec{c} = - 1$ ，则 $| \vec{b} + \vec{c} |$ 的最小值为（）

A、1 B、 $\sqrt{2}$ C、2 D、4

查看试题解析

二、多选题

9. 已知 $A B$ 为圆 $C ： x^{2} + y^{2} = 4$ 的直径，直线 $l ： y = k x + 1$ 与y轴交于点 $M$ ，则（）

A、l与C恒有公共点 B、 $△ A B M$ 是钝角三角形 C、 $△ A B M$ 的面积的最大值为1 D、l被C截得的弦的长度的最小值为 $2 \sqrt{3}$

查看试题解析
10. 已知函数 $f (x) = s i n x c o s x ， g (x) = s i n x + c o s x$ ，则（）

A、 $f (x)$ 与 $g (x)$ 均在 $(0 ， \frac{π}{4})$ 单调递增 B、 $f (x)$ 的图象可由 $g (x)$ 的图象平移得到 C、 $f (x)$ 图象的对称轴均为 $g (x)$ 图象的对称轴 D、函数 $y = f (x) + g (x)$ 的最大值为 $\frac{1}{2} + \sqrt{2}$

查看试题解析
11. 在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = A D = 2$ ， $A A_{1} = 1$ ，点 $P$ 、 $Q$ 在底面 $A_{1}^{} B_{1}^{} C_{1}^{} D_{1}^{}$ 内，直线 $A P$ 与该长方体的每一条棱所成的角都相等，且 $A P ⊥ C Q$ ，则（）

A、 $A P = \sqrt{2}$ B、点 $Q$ 的轨迹长度为 $\sqrt{2}$ C、三棱锥 $D - A_{1} Q B$ 的体积为定值 D、 $A P$ 与该长方体的每个面所成的角都相等

查看试题解析
12. 某商场设有电子盲盒机，每个盲盒外观完全相同，规定每个玩家只能用一个账号登陆，且每次只能随机选择一个开启．已知玩家第一次抽盲盒，抽中奖品的概率为 $\frac{2}{7}$ ，从第二次抽盲盒开始，若前一次没抽中奖品，则这次抽中的概率为 $\frac{1}{2}$ ，若前一次抽中奖品，则这次抽中的概率为 $\frac{1}{3}$ ．记玩家第 $n$ 次抽盲盒，抽中奖品的概率为 $P_{n}$ ，则（）

A、 $P_{2} = \frac{19}{42}$ B、数列 ${P_{n} - \frac{3}{7}}$ 为等比数列 C、 $P_{n} \leq \frac{19}{42}$ D、当 $n \geq 2$ 时， $n$ 越大， $P_{n}$ 越小

查看试题解析

三、填空题

13. 设随机变量 $X \sim N (72 ， σ^{2})$ ，若 $P (70 < X < 73) = 0.3$ ，则 $P (71 < X < 74) =$ ．

查看试题解析
14. 已知 $(x + m)^{6} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + a_{5} x^{5} + a_{6} x^{6}$ ，且 $a_{3} + a_{6} = 1$ 则 $m =$ ．

查看试题解析
15. 已知函数 $f (x) = | e^{x} - 1 | - a x$ 有两个零点，则实数a的取值范围为．

查看试题解析
16. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1} ， F_{2} ， C$ 的渐近线与圆 $x^{2} + y^{2} = a^{2}$ 在第一象限的交点为M，线段 $M F_{2}$ 与C交于点N，O为坐标原点．若 $M F_{1} / / O N$ ，则C的离心率为．

查看试题解析

四、解答题

17. 在 $△ A B C$ 中，角A，B，C所对的边分别为a，b，c， $(a + c) s i n A = s i n A + s i n C$ ， $c^{2} + c = b^{2} - 1$ ．

(1)、求B；

(2)、已知D为 $A C$ 的中点， $B D = \frac{\sqrt{3}}{2}$ ，求 $△ A B C$ 的面积．

查看试题解析
18. 已知 ${a_{n}}$ 为等差数列，且 $a_{n + 1} = 2 a_{n} - 2 n + 3$ ．

(1)、求 ${a_{n}}$ 的首项和公差；

(2)、数列 ${b_{n}}$ 满足 $b_{n} = {\begin{array}{l} \frac{1}{a_{k} \cdot a_{k + 1}} ， n = 3 k - 2 \\ {(- 1)}^{n} \cdot a_{n} ， 3 k - 1 \leq n \leq 3 k \end{array}$ ，其中 $k$ 、 $n \in N^{*}$ ，求 $\sum_{i = 1}^{60} b_{i}$ ．

查看试题解析
19. 如图，三棱台 $A B C - A_{1} B_{1} C_{1}$ 中， $A B = B C = 2 B_{1} C_{1} = 2 ， D$ 是 $A C$ 的中点，E是棱 $B C$ 上的动点．

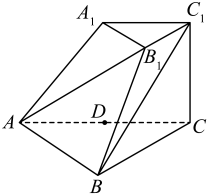(1)、试确定点E的位置，使 $A B_{1} / /$ 平面 $D E C_{1}$ ；

(2)、已知 $A B ⊥ B C_{1} ， C C_{1} ⊥$ 平面 $A B C$ ．设直线 $B C_{1}$ 与平面 $D E C_{1}$ 所成的角为 $θ$ ，试在（1）的条件下，求 $c o s θ$ 的最小值．

查看试题解析
20. 港珠澳大桥海底隧道是当今世界上埋深最大、综合技术难度最高的沉管隧道，建设过程中突破了许多世界级难题，其建成标志着我国在隧道建设领域已达到世界领先水平．在开挖隧道施工过程中，若隧道拱顶下沉速率过快，无法保证工程施工的安全性，则需及时调整支护参数、某施工队对正在施工的隧道工程进行下沉量监控量测工作，通过对监控量测结果进行回归分析，建立前t天隧道拱顶的累加总下沉量z（单位：毫米）与时间t（单位：天）的回归方程，通过回归方程预测是否需要调整支护参数．已知该隧道拱顶下沉的实测数据如下表所示：
t
1
2
3
4
5
6
7
z
0.01
0.04
0.14
0.52
1.38
2.31
4.3
研究人员制作相应散点图，通过观察，拟用函数 $z = k e^{b t}$ 进行拟合．令 $u = l n z$ ，计算得： $\bar{z} = 1.24$ ， $\sum_{i = 1}^{7} (t_{i} - \bar{t}) (z_{i} - \bar{z}) = 22.37$ ， $\sum_{i = 1}^{7} {(z_{i} - \bar{z})}^{2} = 27.5$ ； $\bar{u} = - 1.2$ ， $\sum_{i = 1}^{7} (t_{i} - \bar{t}) (u_{i} - \bar{u}) = 25.2$ ， $\sum_{i = 1}^{7} {(u_{i} - \bar{u})}^{2} = 30$ ．
附：①相关系数 $r = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2} \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}$ ；
②回归直线 $\hat{y} = \hat{a} + \hat{b} x$ 中斜率和截距的最小二乘估计公式分别为：
$\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}} ， \hat{a} = \bar{y} - \hat{b} \bar{x}$
③参考数据： $\sqrt{210} \approx 14.5$ ， $l n 10 \approx 2.30$ ．

(1)、请判断是否可以用线性回归模型拟合u与t的关系；（通常 $| r | > 0.75$ 时，认为可以用线性回归模型拟合变量间的关系）

(2)、试建立z与t的回归方程，并预测前8天该隧道拱顶的累加总下沉量；

(3)、已知当拱顶下沉速率超过9毫米/天，支护系统将超负荷，隧道有塌方风险．若规定每天下午6点为调整支护参数的时间，试估计最迟在第几天需调整支护参数，才能避免塌方．

查看试题解析
21. 已知椭圆 $C ： \frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ 的左、右顶点分别为A，B．直线l与C相切，且与圆 $O ： x^{2} + y^{2} = 4$ 交于M，N两点，M在N的左侧．

(1)、若 $| M N | = \frac{4 \sqrt{5}}{5}$ ，求l的斜率；

(2)、记直线 $A M ， B N$ 的斜率分别为 $k_{1} ， k_{2}$ ，证明： $k_{1} k_{2}$ 为定值．

查看试题解析
22. 已知 $f (x) = \frac{1}{2} x^{2} - a (x - 1) - x l n x$ 有两个极值点 $x_{1}$ 、 $x_{2}$ ，且 $x_{1} < x_{2}$ ．

(1)、求 $a$ 的范围；

(2)、当 $0 < a \leq 1 - l n 2$ 时，证明： $a + \frac{1}{2} < f (x_{1}) + f (x_{2}) < 1$ ．

查看试题解析

t	1	2	3	4	5	6	7
z	0.01	0.04	0.14	0.52	1.38	2.31	4.3