福建省莆田市2023届高三下学期数学3月第二次教学质量检测试卷
试卷更新日期:2023-03-31 类型:高考模拟
一、单选题
-
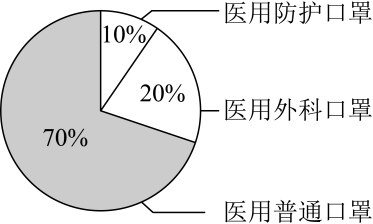
1. 设全集 , , 则( )A、 B、 C、 D、2. 设i为虚数单位, , 则( )A、1 B、 C、 D、23. 某医用口罩生产厂家生产医用普通口罩、医用外科口罩、医用防护口罩三种产品,三种产品的生产比例如图所示,且三种产品中绑带式口罩的比例分别为90%,50%,40%.若从该厂生产的口罩中任选一个,则选到绑带式口罩的概率为( )
 A、0.23 B、0.47 C、0.53 D、0.774. 已知F为抛物线的焦点,A为C上的一点,中点的横坐标为2,则( )A、3 B、4 C、5 D、65. 若 , 则( )A、是等差数列 B、是等比数列 C、是等差数列 D、是等比数列6. 某校科技社利用3D打印技术制作实心模型.如图,该模型的上部分是半球,下部分是圆台.其中半球的体积为 , 圆台的上底面半径及高均是下底面半径的一半.打印所用原料密度为 , 不考虑打印损耗,制作该模型所需原料的质量约为( )()
A、0.23 B、0.47 C、0.53 D、0.774. 已知F为抛物线的焦点,A为C上的一点,中点的横坐标为2,则( )A、3 B、4 C、5 D、65. 若 , 则( )A、是等差数列 B、是等比数列 C、是等差数列 D、是等比数列6. 某校科技社利用3D打印技术制作实心模型.如图,该模型的上部分是半球,下部分是圆台.其中半球的体积为 , 圆台的上底面半径及高均是下底面半径的一半.打印所用原料密度为 , 不考虑打印损耗,制作该模型所需原料的质量约为( )() A、 B、 C、 D、7. 已知函数 , 将其图象向左平移个单位长度,得到函数的图象.的顶点都是与图象的公共点,则面积的最小值为( )A、 B、 C、 D、8. 在正方体中,点M,N分别是上的动点,当线段的长最小时,直线与平面所成角的正弦值为( )A、 B、 C、 D、
A、 B、 C、 D、7. 已知函数 , 将其图象向左平移个单位长度,得到函数的图象.的顶点都是与图象的公共点,则面积的最小值为( )A、 B、 C、 D、8. 在正方体中,点M,N分别是上的动点,当线段的长最小时,直线与平面所成角的正弦值为( )A、 B、 C、 D、二、多选题
-
9. 已知圆 , 点 , 点M在x轴上,则( )A、B不在圆C上 B、y轴被圆C截得的弦长为3 C、A,B,C三点共线 D、的最大值为10. “50米跑”是《国家学生体质健康标准》测试项目中的一项,某地区高三男生的“50米跑”测试成绩(单位:秒)服从正态分布 , 且 . 从该地区高三男生的“50米跑”测试成绩中随机抽取3个,其中成绩在间的个数记为X,则( )A、 B、 C、 D、11. 已知正四面体的棱长为 , S是及其内部的点构成的集合.若 , 集合 , 则T表示的区域可以是( )A、
 B、
B、 C、
C、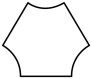 D、
D、 12. 已知函数的定义域为R,且为偶函数,则( )A、 B、为偶函数 C、 D、
12. 已知函数的定义域为R,且为偶函数,则( )A、 B、为偶函数 C、 D、三、填空题
-
13. 已知向量 , 为单位向量, , 的夹角为 , 则 .14. 的展开式中的系数为(用数字作答)15. 直线l经过点 , 且与曲线相切,写出l的一个方程 .16. 已知椭圆的上、下顶点分别为A,B,右焦点为F,B关于直线的对称点为 . 若过A, , F三点的圆的半径为a,则C的离心率为 .
四、解答题
-
17. 已知正项数列满足 .(1)、求的通项公式;(2)、设 , 记数列的前n项和为 , 证明: .18. 的内角A,B,C的对边分别为a,b,c, , D为的中点,且 .(1)、证明:;(2)、若 , 求的面积.19. 如图,直三棱柱的侧面为正方形, , E,F分别为 , 的中点, .
 (1)、证明:平面;(2)、求平面与平面夹角的余弦值.20. 互花米草是禾本科草本植物,其根系发达,具有极高的繁殖系数,对近海生态具有较大的危害.为尽快消除互花米草危害,2022年10月24日,市政府印发了《莆田市互花米草除治攻坚实施方案》,对全市除治攻坚行动做了具体部署.某研究小组为了解甲、乙两镇的互花米草根系分布深度情况,采用按比例分层抽样的方法抽取样本.已知甲镇的样本容量 , 样本平均数 , 样本方差;乙镇的样本容量 , 样本平均数 , 样本方差 .
(1)、证明:平面;(2)、求平面与平面夹角的余弦值.20. 互花米草是禾本科草本植物,其根系发达,具有极高的繁殖系数,对近海生态具有较大的危害.为尽快消除互花米草危害,2022年10月24日,市政府印发了《莆田市互花米草除治攻坚实施方案》,对全市除治攻坚行动做了具体部署.某研究小组为了解甲、乙两镇的互花米草根系分布深度情况,采用按比例分层抽样的方法抽取样本.已知甲镇的样本容量 , 样本平均数 , 样本方差;乙镇的样本容量 , 样本平均数 , 样本方差 .参考数据: .
(1)、求由两镇样本组成的总样本的平均数及其方差;(2)、为营造“广泛发动、全民参与”的浓厚氛围,甲、乙两镇决定进行一次“互花米草除治大练兵”比赛,两镇各派一支代表队参加,经抽签确定第一场在甲镇举行.比赛规则:每场比赛直至分出胜负为止,胜方得1分,负方得0分,下一场在负方举行,先得2分的代表队获胜,比赛结束.
当比赛在甲镇举行时,甲镇代表队获胜的概率为 , 当比赛在乙镇举行时,甲镇代表队获胜的概率为 . 假设每场比赛结果相互独立.甲镇代表队的最终得分记为X,求 .