山东省临沂市兰陵县2022年九年级中考数学二模试题
试卷更新日期:2023-03-31 类型:中考模拟
一、单选题
-
1. 在-3,2,-1,3这四个数中,比-2小的数是( )A、-3 B、2 C、-1 D、32. 下列冬奥运会图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的制造工艺达到了 米,用科学记数法表示 为( )A、 B、 C、 D、4. 如图,直线l1 ∥ l2 , CD⊥AB于点D ,∠1=50°,则∠BCD的度数为( )
3. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的制造工艺达到了 米,用科学记数法表示 为( )A、 B、 C、 D、4. 如图,直线l1 ∥ l2 , CD⊥AB于点D ,∠1=50°,则∠BCD的度数为( ) A、40° B、45° C、50° D、30°5. 下列计算错误的是( )A、 B、 C、 D、6. 在平面直角坐标系中,将点P (−x,1−x)先向右平移3个单位得点P1 , 再将P1向下平移3个单位得点P2 , 若点P2落在第四象限,则x的取值范围是( )A、 B、 C、 D、或7. 计算:的结果是( )A、 B、 C、 D、8. 某班从张强、李硕、郭凯、夏雪四人中随机抽取两人参加羽毛球比赛,则两人恰好是张强和李硕的概率是( )A、 B、 C、 D、9. 某班组织学生去距学校16千米的科技馆参观,一部分同学骑自行车先走,走了20分钟后,其余同学乘汽车出发,结果他们同时到达.已知汽车的平均速度是骑车同学的3倍,设骑车同学的平均速度是x千米/时,则下列方程正确的是( )A、 B、 C、 D、10. 已知二次函数y=(x+m)2–n的图象如图所示,则一次函数y=mx+n与反比例函数y= 的图象可能是( )
A、40° B、45° C、50° D、30°5. 下列计算错误的是( )A、 B、 C、 D、6. 在平面直角坐标系中,将点P (−x,1−x)先向右平移3个单位得点P1 , 再将P1向下平移3个单位得点P2 , 若点P2落在第四象限,则x的取值范围是( )A、 B、 C、 D、或7. 计算:的结果是( )A、 B、 C、 D、8. 某班从张强、李硕、郭凯、夏雪四人中随机抽取两人参加羽毛球比赛,则两人恰好是张强和李硕的概率是( )A、 B、 C、 D、9. 某班组织学生去距学校16千米的科技馆参观,一部分同学骑自行车先走,走了20分钟后,其余同学乘汽车出发,结果他们同时到达.已知汽车的平均速度是骑车同学的3倍,设骑车同学的平均速度是x千米/时,则下列方程正确的是( )A、 B、 C、 D、10. 已知二次函数y=(x+m)2–n的图象如图所示,则一次函数y=mx+n与反比例函数y= 的图象可能是( )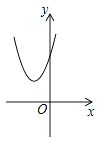 A、
A、 B、
B、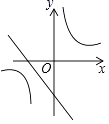 C、
C、 D、
D、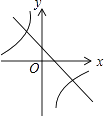 11. 如图,二次函数的图象经过点 , , 与y轴交于点C.下列结论:①;②当时,y随x的增大而增大;③3b=2c;④抛物线顶点坐标为 , 则关于x的方程有实数根.其中正确的个数有( )
11. 如图,二次函数的图象经过点 , , 与y轴交于点C.下列结论:①;②当时,y随x的增大而增大;③3b=2c;④抛物线顶点坐标为 , 则关于x的方程有实数根.其中正确的个数有( )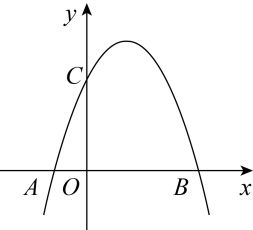 A、1个 B、2个 C、3个 D、4个12. 如图,在⊙O中,AB是⊙O的直径,AB=10, , 点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=30°;②∠DOB=2∠CED;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A、1个 B、2个 C、3个 D、4个12. 如图,在⊙O中,AB是⊙O的直径,AB=10, , 点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=30°;②∠DOB=2∠CED;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )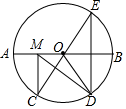 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 若在实数范围内有意义,则x的取值范围是 .14. 已知a−3b=2,ab=3,则2a3b−12a2b2+18ab3= .15. 如图,在矩形ABCD中,AD=2.将∠A向内翻折,点A落在BC上,记为 , 折痕为DE.若将∠B沿向内翻折,点B恰好落在DE上,记为 , 则AB=.
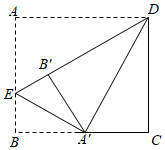 16. 在平面直角坐标系中,对于点P(x,y)和点Q(x,y′),给出如下定义:若 , 则称点Q是点P的限变点.例如(2,3)的限变点是(2,2);(−5,−4)的限变点是(−5,4).若点P(x,y)在二次函数y=x2−2x−8的图像上(x轴下方),则其限变点Q的纵坐标y′的取值范围是 .
16. 在平面直角坐标系中,对于点P(x,y)和点Q(x,y′),给出如下定义:若 , 则称点Q是点P的限变点.例如(2,3)的限变点是(2,2);(−5,−4)的限变点是(−5,4).若点P(x,y)在二次函数y=x2−2x−8的图像上(x轴下方),则其限变点Q的纵坐标y′的取值范围是 .三、解答题
-
17. 计算: .18. 为了激励青少年学习国学的热情,弘扬优秀的中国传统文化.某校组织了国学益智竞赛节目.竞赛中将成绩分为:A(优秀)、B(良好)、C(合格)、D(不合格)四个等级.张老师随机调查了部分同学的竞赛成绩,绘制了如下统计图.
 (1)、本次抽样调查的样本容量是 ▲ , 请补全条形统计图;(2)、已知调查对象中只有三位男生竞赛成绩不合格,张老师准备随机回访两位竞赛成绩不合格的同学,请用树状图或列表法求出恰好回访到一男一女的概率;(3)、该校共有2200名学生,请你估计该校竞赛成绩“优秀”的学生人数.19. 2022年2月4日,举世瞩目的北京冬奥会在北京鸟巢盛大开幕.为全力做好冬奥会的安保维稳工作,为冬奥会增光添彩,负责安保的工作人员在奥运会开始前进行了多次演习,确保万无一失.演习之一模拟了越野滑雪项目可能发生的安全事故,为了方便确定假人具体位置,安保人员在C处向上放出一架搜救无人机,该无人机以每分钟50m的速度沿着仰角为45°的方向上升,8分钟后升到B处.此时,安保人员通过无人机发现假人在安保人员的正东方向,且从无人机上看,假人在它的俯角为60°方向,求安保人员与假人之间AC的距离.(结果保留根号).
(1)、本次抽样调查的样本容量是 ▲ , 请补全条形统计图;(2)、已知调查对象中只有三位男生竞赛成绩不合格,张老师准备随机回访两位竞赛成绩不合格的同学,请用树状图或列表法求出恰好回访到一男一女的概率;(3)、该校共有2200名学生,请你估计该校竞赛成绩“优秀”的学生人数.19. 2022年2月4日,举世瞩目的北京冬奥会在北京鸟巢盛大开幕.为全力做好冬奥会的安保维稳工作,为冬奥会增光添彩,负责安保的工作人员在奥运会开始前进行了多次演习,确保万无一失.演习之一模拟了越野滑雪项目可能发生的安全事故,为了方便确定假人具体位置,安保人员在C处向上放出一架搜救无人机,该无人机以每分钟50m的速度沿着仰角为45°的方向上升,8分钟后升到B处.此时,安保人员通过无人机发现假人在安保人员的正东方向,且从无人机上看,假人在它的俯角为60°方向,求安保人员与假人之间AC的距离.(结果保留根号). 20. 在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2
20. 在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2 (1)、y关于x的函数关系式是 , x的取值范围是;(2)、在平面直角坐标系中画出该函数图象;(3)、将直线y=-x+2向上平移a(a>0)个单位长度后与上述函数图象有且只有一个交点,请求出此时a的值.21. 如图Rt△ABC中,∠C=90°,AD平分∠BAC,AD交BC于点D,点E在AB上,以AE为直径的⊙O经过点D.
(1)、y关于x的函数关系式是 , x的取值范围是;(2)、在平面直角坐标系中画出该函数图象;(3)、将直线y=-x+2向上平移a(a>0)个单位长度后与上述函数图象有且只有一个交点,请求出此时a的值.21. 如图Rt△ABC中,∠C=90°,AD平分∠BAC,AD交BC于点D,点E在AB上,以AE为直径的⊙O经过点D.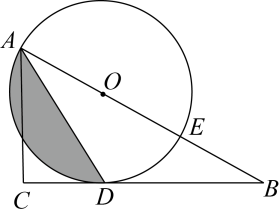 (1)、求证:直线BC是⊙O的切线.(2)、若AC=6,∠B=30°,求图中阴影部分的面积.22. 已知二次函数: .
(1)、求证:直线BC是⊙O的切线.(2)、若AC=6,∠B=30°,求图中阴影部分的面积.22. 已知二次函数: . (1)、该二次函数图象的对称轴是 , 它恒经过两个定点的坐标为;(2)、在直角坐标系中,点 、点 ,若此二次函数的图象与线段 恰有一个公共点,结合图象,求a的取值范围.(3)、若该二次函数的最大值为4.
(1)、该二次函数图象的对称轴是 , 它恒经过两个定点的坐标为;(2)、在直角坐标系中,点 、点 ,若此二次函数的图象与线段 恰有一个公共点,结合图象,求a的取值范围.(3)、若该二次函数的最大值为4.①求二次函数的表达式;
②当 时,函数的最大值为m,最小值为n,若 ,求t的值.
23.如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
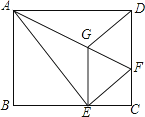 (1)、求证:四边形EFDG是菱形;(2)、探究线段EG、GF、AF之间的数量关系,并说明理由;(3)、若AG=6,EG=2 ,求BE的长.
(1)、求证:四边形EFDG是菱形;(2)、探究线段EG、GF、AF之间的数量关系,并说明理由;(3)、若AG=6,EG=2 ,求BE的长.