山东省淄博市张店区2022年中考二模数学试题
试卷更新日期:2023-03-31 类型:中考模拟
一、单选题
-
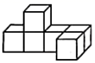
1. ﹣3的相反数是( )A、 B、 C、-3 D、32. 如图所示的几何体是由6个大小相同的小立方块搭成,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列各式中,化简正确的是 ( )A、 B、 C、 D、4. 如图,直线 , 将含有45°角的三角板的直角顶点放在直线上,顶点放在直线上,若 , 则∠2的度数为( )
3. 下列各式中,化简正确的是 ( )A、 B、 C、 D、4. 如图,直线 , 将含有45°角的三角板的直角顶点放在直线上,顶点放在直线上,若 , 则∠2的度数为( ) A、45° B、17° C、25° D、30°5. 中国象棋文化历史久远.在图中所示的部分棋盘中,“馬”的位置在“---”(图中虚线)的下方,“馬”移动一次能够到达的所有位置已用“●”标记,则“馬”随机移动一次,到达的位置在“---”上方的概率是( )
A、45° B、17° C、25° D、30°5. 中国象棋文化历史久远.在图中所示的部分棋盘中,“馬”的位置在“---”(图中虚线)的下方,“馬”移动一次能够到达的所有位置已用“●”标记,则“馬”随机移动一次,到达的位置在“---”上方的概率是( ) A、 B、 C、 D、6. 如图,在矩形中放入正方形 , 正方形 , 正方形 , 点E在上,点M、N在上,若 , , , 则图中右上角阴影部分的周长与左下角阴影部分的周长的差为( )
A、 B、 C、 D、6. 如图,在矩形中放入正方形 , 正方形 , 正方形 , 点E在上,点M、N在上,若 , , , 则图中右上角阴影部分的周长与左下角阴影部分的周长的差为( ) A、5 B、6 C、7 D、87. 甲、乙、丙、丁四人进行射击测试,他们在相同条件下各射击10次,成绩(单位:环)统计如表:
A、5 B、6 C、7 D、87. 甲、乙、丙、丁四人进行射击测试,他们在相同条件下各射击10次,成绩(单位:环)统计如表:甲
乙
丙
丁
平均数
9.6
9.5
9.5
9.6
方差
0.28
0.27
0.25
0.25
若从这四人中,选出一位成绩较好且状态稳定的选手参加比赛,那么应选( )
A、甲 B、乙 C、丙 D、丁8. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根9. 如图,矩形中,对角线的垂直平分线分别交 , 于点E,F,若 , , 则的值为( ) A、 B、 C、 D、10. 在平面直角坐标系中,点在抛物线上,当时,下列说法一定正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则11. 如图,内切于 , 点P、点Q分别在直角边、斜边上, , 且与相切,若 , 则的值为( )
A、 B、 C、 D、10. 在平面直角坐标系中,点在抛物线上,当时,下列说法一定正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则11. 如图,内切于 , 点P、点Q分别在直角边、斜边上, , 且与相切,若 , 则的值为( ) A、 B、 C、 D、12. 如图,在平面直角坐标系中,点A的坐标是 , 点C的坐标是 , 点是x轴上的动点,点B在x轴上移动时,始终保持是等边三角形(点P不在第二象限),连接 , 求得的最小值为( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中,点A的坐标是 , 点C的坐标是 , 点是x轴上的动点,点B在x轴上移动时,始终保持是等边三角形(点P不在第二象限),连接 , 求得的最小值为( )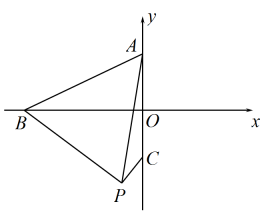 A、 B、4 C、 D、2
A、 B、4 C、 D、2二、填空题
-
13. 现实生活中经常用正数和负数来表示具有相反意义的量.如果收入50元记作+50元,那么支出20元应记作元.14. 若 , 则 .15. 如图,在Rt△ABC中,∠C=90°,以顶点B为圆心,适当长度为半径画弧,分别交AB,BC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D.若tan∠A= , 则 .
 16. 如图,半圆的直径 , 弦 , 把沿直线对折,且恰好落在上,则的长为 .
16. 如图,半圆的直径 , 弦 , 把沿直线对折,且恰好落在上,则的长为 . 17. 两个反比例函数 , 在第一象限内的图象如图所示,点 , , , …,在反比例函数图象上,它们的横坐标分别是 , , , …, , 纵坐标分别是1,3,5,…,共2022个连续奇数,过点 , , , …,分别作y轴的平行线,与的图象交点依次是 , , , …, , 过点 , , , …,分别作x轴的平行线,与y轴的交点依次是 , , , …, , 连接 , , , …, , 则的面积 , 且点的纵坐标 .
17. 两个反比例函数 , 在第一象限内的图象如图所示,点 , , , …,在反比例函数图象上,它们的横坐标分别是 , , , …, , 纵坐标分别是1,3,5,…,共2022个连续奇数,过点 , , , …,分别作y轴的平行线,与的图象交点依次是 , , , …, , 过点 , , , …,分别作x轴的平行线,与y轴的交点依次是 , , , …, , 连接 , , , …, , 则的面积 , 且点的纵坐标 .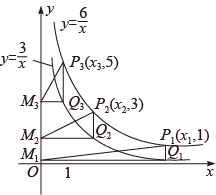
三、解答题
-
18. 解不等式组 , 把它的解集表示在数轴上,并求出这个不等式组的整数解.19. 如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC上,且BE=CF,BD=CE.
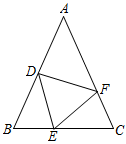 (1)、求证:△DEF是等腰三角形;(2)、当∠A=60°时,求∠EDF的度数;20. 如图,已知一次函数y1=kx+b的图像与反比例函数y2=图像交于点A(4,1)和点B(a,−2).
(1)、求证:△DEF是等腰三角形;(2)、当∠A=60°时,求∠EDF的度数;20. 如图,已知一次函数y1=kx+b的图像与反比例函数y2=图像交于点A(4,1)和点B(a,−2). (1)、求一次函数与反比例函数的解析式;(2)、当时,直接写出自变量x的取值范围;(3)、如果在x轴上找一点C使△ABC的面积为8,求点C坐标.21. 2022年北京冬奥会的举办促进了冰雪旅游,小明为了解寒假期间冰雪旅游的消费情况,从甲、乙两个滑雪场的游客中各随机抽取了50人,获得了这些游客当天消费额(单位:元)的数据,并对数据进行整理、描述和分析.下面给出部分信息:a.甲滑雪场游客消费额的数据的频数分布直方图如下(数据分成6组: , , , , , ):
(1)、求一次函数与反比例函数的解析式;(2)、当时,直接写出自变量x的取值范围;(3)、如果在x轴上找一点C使△ABC的面积为8,求点C坐标.21. 2022年北京冬奥会的举办促进了冰雪旅游,小明为了解寒假期间冰雪旅游的消费情况,从甲、乙两个滑雪场的游客中各随机抽取了50人,获得了这些游客当天消费额(单位:元)的数据,并对数据进行整理、描述和分析.下面给出部分信息:a.甲滑雪场游客消费额的数据的频数分布直方图如下(数据分成6组: , , , , , ):
b.甲滑雪场游客消费额的数据在这一组的是:
410 430 430 440 440 440 450 450 520 540
c.甲、乙两个滑雪场游客消费额的数据的平均数、中位数如下:
平均数
中位数
甲滑雪场
420
m
乙滑雪场
390
n
根据以上信息,回答下列问题:
(1)、写出表中m的值;(2)、一名被调查的游客当天的消费额为380元,在他所在的滑雪场,他的消费额超过了一半以上的被调查的游客,那么他是哪个滑雪场的游客?请说明理由;(3)、若乙滑雪场当天的游客人数为500人,估计乙滑雪场这个月(按30天计算)的游客消费总额.22. 某市新建的自行车道已成为该市一道亮丽的风景线(如图1所示).在建设自行车道的过程中,为了解决与自行车道相连接的天桥坡度过陡的问题,施工方对这一天桥进行了改造,在原有坡道的右侧架设了一条“之”字形自行车专用坡道(折线 , 如图2所示),并在其上安装了自行车助力系统,上行设置有自行车传送带,降低推行难度;下行设置有阻力装置,提高安全性.其中支柱 , 均垂直于地面. (1)、已知支柱为15米,为6米,坡道的坡度 , 则坡道的长度是多少米?(结果精确到0.1米,参考数据: , , ;注:坡度是指坡面的铅直高度与水平宽度的比)(2)、现已知自行车道的全长为75千米,为了保证骑行爱好者的交通安全,车道设计的骑行最高速度不得超过m千米/时.若以最高限速的的速度骑行,则骑行完整个路程比用最高限速速度骑行时多小时,求m的值.23. 已知,矩形ABCD,点E在AB上,点G在AD,点F在射线BC上,点H在CD上.
(1)、已知支柱为15米,为6米,坡道的坡度 , 则坡道的长度是多少米?(结果精确到0.1米,参考数据: , , ;注:坡度是指坡面的铅直高度与水平宽度的比)(2)、现已知自行车道的全长为75千米,为了保证骑行爱好者的交通安全,车道设计的骑行最高速度不得超过m千米/时.若以最高限速的的速度骑行,则骑行完整个路程比用最高限速速度骑行时多小时,求m的值.23. 已知,矩形ABCD,点E在AB上,点G在AD,点F在射线BC上,点H在CD上. (1)、如图1,当矩形ABCD为正方形时,且DE⊥GF,求证:BF=AE+AG;(2)、在(1)的条件下,将GF沿AD向右平移至点G与点D重合,如图2,连接EF,取EF的中点P,连接PC,试判断BE与PC的数量关系,并说明理由;(3)、如图3,点F在BC上,连接EH,EH交FG于O,∠GOH=45°,若AB=2,BC=4,FG= , 求线段EH的长.24. 如图,在平面直角坐标系中,点O为坐标原点,抛物线与x轴交于点 , 点 , 与y轴交于点C,连接 , 点P在第二象限的抛物线上,连接、 , 线段交线段于点E.
(1)、如图1,当矩形ABCD为正方形时,且DE⊥GF,求证:BF=AE+AG;(2)、在(1)的条件下,将GF沿AD向右平移至点G与点D重合,如图2,连接EF,取EF的中点P,连接PC,试判断BE与PC的数量关系,并说明理由;(3)、如图3,点F在BC上,连接EH,EH交FG于O,∠GOH=45°,若AB=2,BC=4,FG= , 求线段EH的长.24. 如图,在平面直角坐标系中,点O为坐标原点,抛物线与x轴交于点 , 点 , 与y轴交于点C,连接 , 点P在第二象限的抛物线上,连接、 , 线段交线段于点E. (1)、求抛物线的表达式;(2)、若的面积为 , 的面积为 , 当时,求点P的坐标;(3)、已知点C关于抛物线对称轴的对称点为点N,连接 , 点H在x轴上,当时,
(1)、求抛物线的表达式;(2)、若的面积为 , 的面积为 , 当时,求点P的坐标;(3)、已知点C关于抛物线对称轴的对称点为点N,连接 , 点H在x轴上,当时,①求满足条件的所有点H的坐标
②当点H在线段上时,点Q是平面直角坐标系内一点,保持 , 连接 , 将线段绕着点Q顺时针旋转90°,得到线段 , 连接 , 请直接写出线段的取值范围.