山东省淄博市沂源县2022年中考二模数学试题
试卷更新日期:2023-03-31 类型:中考模拟
一、单选题
-
1. 下列四个图形中,既是轴对称图形又是中心对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中,由能得到的是( )A、
2. 下列图形中,由能得到的是( )A、 B、
B、 C、
C、 D、
D、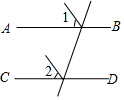 3. 使 有意义的x的取值范围是( )
3. 使 有意义的x的取值范围是( )
A、x≤3 B、x<3 C、x≥3 D、x>34. 下列说法错误的是( )A、了解玉米新品种“农大108”的产量情况适合作抽样调查 B、了解本校八年级2班学生业余爱好适合作普查 C、明天的天气是晴天是随机事件 D、为了解A市20000名学生中考成绩,抽查了500名学生成绩进行统计分析,样本容量是500名5. 命题“关于x的一元二次方程 , 必有实数解.”是假命题.则在下列选项中,可以作为反例的是( ).A、 B、 C、 D、6. 为了参加全校文艺演出,某年级组建了46人的合唱队和30人的舞蹈队,现根据演出需要,从舞蹈队中抽调了部分同学参加合唱队,使合唱队的人数恰好是舞蹈队的人数的3倍.设从舞蹈队中抽调了x人参加合唱队,可得正确的方程是( )A、3(46-x)=30+x B、46+x=3(30-x) C、46-3x=30+x D、46-x=3(30-x)7. 如图,四边形中, , , , 点 , 分别为线段 , 上的动点(含端点,但点不与点重合),点 , 分别为 , 的中点,则长度的最大值为( ) A、8 B、7 C、6 D、58. 如图1,已知平行四边形ABCD中,点E是AB边上的一动点(与点A不重合),设AE=x,DE的延长线交CB的延长线于点F,设BF=y,且y与x之间的函数关系图象如图2所示,则下面的结论中错误的是( )
A、8 B、7 C、6 D、58. 如图1,已知平行四边形ABCD中,点E是AB边上的一动点(与点A不重合),设AE=x,DE的延长线交CB的延长线于点F,设BF=y,且y与x之间的函数关系图象如图2所示,则下面的结论中错误的是( ) A、 B、当时, C、若 , 则 D、若 , 则9. 如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂长2米,且与灯柱成角,路灯采用圆锥形灯罩,灯罩的轴线与灯臂垂直,当灯罩的轴线通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱高度应该设计为( ).
A、 B、当时, C、若 , 则 D、若 , 则9. 如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂长2米,且与灯柱成角,路灯采用圆锥形灯罩,灯罩的轴线与灯臂垂直,当灯罩的轴线通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱高度应该设计为( ).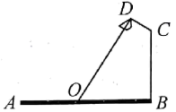 A、米 B、米 C、米 D、米10. 如图,兰博基尼某车型车门设计属于剪刀门设计,即车门关闭时位置如图中四边形ABCD,车门打开是绕点A逆时针旋转至CD与AD垂直,已知四边形ABCD与四边形AB′C′D′在同一平面,若AD∥BC,∠D=45°,∠DAB′=30°,CD=60cm,则AB的长约为( )(≈1.7)
A、米 B、米 C、米 D、米10. 如图,兰博基尼某车型车门设计属于剪刀门设计,即车门关闭时位置如图中四边形ABCD,车门打开是绕点A逆时针旋转至CD与AD垂直,已知四边形ABCD与四边形AB′C′D′在同一平面,若AD∥BC,∠D=45°,∠DAB′=30°,CD=60cm,则AB的长约为( )(≈1.7) A、21cm B、42cm C、51cm D、60cm11.
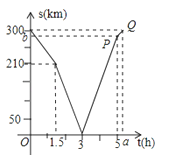
A、21cm B、42cm C、51cm D、60cm11.甲、乙两车分别从M,N两地沿同一公路相向匀速行驶,两车分别抵达N,M两地后即停止行驶.已知乙车比甲车提前出发,设甲、乙两车之间的路程S(km),乙行驶的时间为t(h),S与t的函数关系如图所示.有下列说法:
①M、N两地之间公路路程是300km,两车相遇时甲车恰好行驶3小时;
②甲车速度是80km/h,乙车比甲车提前1.5个小时出发;
③当t=5(h)时,甲车抵达N地,此时乙车离M地还有20km的路程;
④a= , b=280,图中P,Q所在直线与横轴的交点恰( , 0).
其中正确的是( )
 A、①② B、②③ C、③④ D、②④12. 如图所示,矩形ABCD中,AD=a,AB=b,若要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a,b间的关系一定满足( ).
A、①② B、②③ C、③④ D、②④12. 如图所示,矩形ABCD中,AD=a,AB=b,若要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a,b间的关系一定满足( ).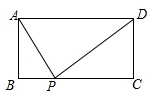 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 据统计,某市志愿者人数已达109万人,将109万人用科学记数法表示应为 .14. 数据a,4,2,5,3的中位数为b,且a和b是方程x2-10x+24=0的两个根,则b是 .15.
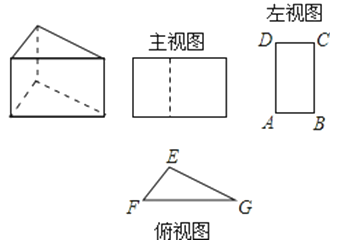
三棱柱的三视图如图所示,△EFG中,EF=8cm,EG=12cm,∠EGF=30°,则AB的长为 cm.
 16. 从 , , , 0,1,2,3这七个数中随机抽取一个数记为a,则a的值是不等式组的解,但不是方程的实数解的概率为 .17. 在平面直角坐标系xOy中,抛物线经过点和 . 将抛物线在A、B之间的部分记为图象M(含A、B两点).将图象M沿直线翻折,得到图象N.若过点的直线与图象M、图象N都相交,且只有两个交点,则b的取值范围 .
16. 从 , , , 0,1,2,3这七个数中随机抽取一个数记为a,则a的值是不等式组的解,但不是方程的实数解的概率为 .17. 在平面直角坐标系xOy中,抛物线经过点和 . 将抛物线在A、B之间的部分记为图象M(含A、B两点).将图象M沿直线翻折,得到图象N.若过点的直线与图象M、图象N都相交,且只有两个交点,则b的取值范围 .三、解答题
-
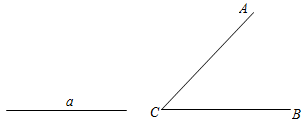
18. 化简:÷(a+1)+ .19. 已知:线段a和 . 求作:点O,使点O在的内部, , 且O到的两边距离相等.
 20. 某运动品牌店对第一季度A、B两款运动服的销售情况进行统计,两款运动服的销售量及总销售额如图所示:
20. 某运动品牌店对第一季度A、B两款运动服的销售情况进行统计,两款运动服的销售量及总销售额如图所示: (1)、一月份A款运动服的销售量是B款的 , 则一月份B款运动服销售了多少件?(2)、根据图中信息,求出这两款运动服的单价.21. 如图,直线与y轴交于A点,与反比例函数的图像交于点M,过M作轴于点H,且 .
(1)、一月份A款运动服的销售量是B款的 , 则一月份B款运动服销售了多少件?(2)、根据图中信息,求出这两款运动服的单价.21. 如图,直线与y轴交于A点,与反比例函数的图像交于点M,过M作轴于点H,且 . (1)、请直接写出k的值;(2)、设点是反比例函数图像上的点,在y轴上是否存在点P,使得最小?若存在,求出点P的坐标;若不存在,请说明理由.22. 在 中, , ,AD是BC边上的高,E,F分别为边AB,AC的中点.当 时,BC边上存在一点Q,使 ,求此时BQ的长.
(1)、请直接写出k的值;(2)、设点是反比例函数图像上的点,在y轴上是否存在点P,使得最小?若存在,求出点P的坐标;若不存在,请说明理由.22. 在 中, , ,AD是BC边上的高,E,F分别为边AB,AC的中点.当 时,BC边上存在一点Q,使 ,求此时BQ的长.