山东省枣庄滕州市2022年中考三模数学试题
试卷更新日期:2023-03-31 类型:中考模拟
一、单选题
-
1. 下列各数中,比大的数是( )A、-3 B、-2 C、-1 D、02. 如图,在数轴上,点A、B分别表示a、b,且 ,若 ,则点A表示的数为( )
 A、-3 B、0 C、3 D、-63. 把直尺与一块三角板如图放置,若 ,则 的度数为( )
A、-3 B、0 C、3 D、-63. 把直尺与一块三角板如图放置,若 ,则 的度数为( )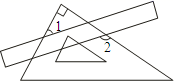 A、 B、 C、 D、4. 如图,直线与相交于点 , 则关于x的方程的解是( )
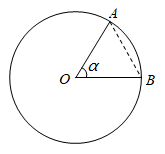
A、 B、 C、 D、4. 如图,直线与相交于点 , 则关于x的方程的解是( ) A、 B、 C、 D、5. 下列说法正确的是( )A、为了了解全国中学生的心理健康情况,选择全面调查 B、在一组数据7,6,5,6,6,4,8中,众数和中位数都是6 C、“若 是实数,则 ”是必然事件 D、若甲组数据的方差 ,乙组数据的方差 ,则乙组数据比甲组数据稳定6. 《九章算术》中有一道题的条件是:“今有大器五一容三斛,大器一小器五容二斛.”大致意思是:有大小两种盛米的桶,5大桶加1小桶共盛3斛米,1大桶加5小桶共盛2斛米,依据该条件,1大桶加1小桶共盛( )斛米.(注:斛是古代一种容量单位)A、 B、 C、1 D、7. 一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若 ,则劣弧AB的长是( )
A、 B、 C、 D、5. 下列说法正确的是( )A、为了了解全国中学生的心理健康情况,选择全面调查 B、在一组数据7,6,5,6,6,4,8中,众数和中位数都是6 C、“若 是实数,则 ”是必然事件 D、若甲组数据的方差 ,乙组数据的方差 ,则乙组数据比甲组数据稳定6. 《九章算术》中有一道题的条件是:“今有大器五一容三斛,大器一小器五容二斛.”大致意思是:有大小两种盛米的桶,5大桶加1小桶共盛3斛米,1大桶加5小桶共盛2斛米,依据该条件,1大桶加1小桶共盛( )斛米.(注:斛是古代一种容量单位)A、 B、 C、1 D、7. 一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若 ,则劣弧AB的长是( )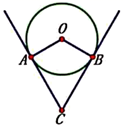 A、 B、 C、 D、8. 如图,过点作两条直线,分别交函数(),()的图像于点 , 点 , 连接 . 若轴,则的面积是( )
A、 B、 C、 D、8. 如图,过点作两条直线,分别交函数(),()的图像于点 , 点 , 连接 . 若轴,则的面积是( )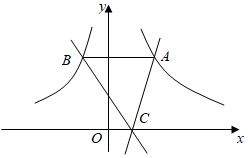 A、3 B、4 C、5 D、69. 如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A、3 B、4 C、5 D、69. 如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( ) A、1 B、 C、2 D、10. 已知二次函数()的图象如图所示,对称轴为直线 , 与轴的一个交点为 . 给出下列结论:①;②;③图象与轴的另一个交点为;④当时,随的增大而减小;⑤不等式的解集是 . 其中正确结论的个数是( )
A、1 B、 C、2 D、10. 已知二次函数()的图象如图所示,对称轴为直线 , 与轴的一个交点为 . 给出下列结论:①;②;③图象与轴的另一个交点为;④当时,随的增大而减小;⑤不等式的解集是 . 其中正确结论的个数是( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 将多项式分解因式为 .12. 在“绿水青山就是金山银山”这句话中任选一个汉字,这个字是“山”的概率.13. 黄金分割在生活中的应用十分广泛,例如大多数窗户的宽和长的比约为0.618,已知某扇窗户的长为1.6米,则宽约为米 . (结果精确到个位)14. 已知实数a、b满足 ,若关于x的一元二次方程 的两个实数根分别为 、 ,则 .15. 弧度是表示角度大小的一种单位,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作 .已知 ,则 与 的大小关系是 .
 16. 如图,在平面直角坐标系中,正方形与正方形是以为位似中心的位似图形,且位似比为 , 点 , , 在x轴上,延长交射线与点 , 以为边作正方形;延长 , 交射线与点 , 以为边作正方形;…按照这样的规律继续作下去,若 , 则正方形的面积为 .
16. 如图,在平面直角坐标系中,正方形与正方形是以为位似中心的位似图形,且位似比为 , 点 , , 在x轴上,延长交射线与点 , 以为边作正方形;延长 , 交射线与点 , 以为边作正方形;…按照这样的规律继续作下去,若 , 则正方形的面积为 .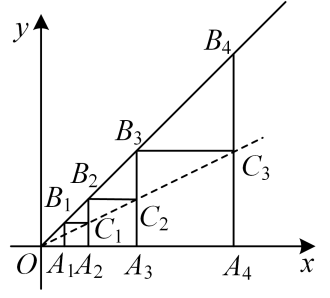
三、解答题
-
17. 先化简,再求值: ,其中18. 用※定义一种新运算:对于任意实数m和n , 规定 ,如: .
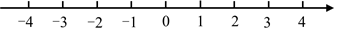 (1)、求 ;(2)、若 ,求m的取值范围,并在所给的数轴上表示出解集.19. 如图,在 中,D是 边上一点,且 .
(1)、求 ;(2)、若 ,求m的取值范围,并在所给的数轴上表示出解集.19. 如图,在 中,D是 边上一点,且 . (1)、尺规作图(保留作图痕迹,不写作法)
(1)、尺规作图(保留作图痕迹,不写作法)①作 的角平分线交 于点E;
②作线段 的垂直平分线交 于点F.
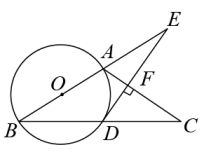
(2)、连接 ,直接写出线段 和 的数量关系及位置关系.20. 2022年冬季奥运会在北京举行,激起了人们对冰雪运动的极大热情.如图是某滑雪场高级雪道缆车线路示意图,滑雪者从点出发,途经点后到达终点 , 其中 , , 且段的运行路线与水平面的夹角为30°,段的运行路线与水平面的夹角为37°,求从点运行到点垂直上升的高度.(结果保留整数;参考数据: , , )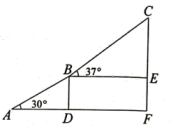 21. 【问题背景】如图1,点、分别在正方形的边、上, , 连接 , 我们可以通过把绕点逆时针旋转90°到 , 容易证得: .
21. 【问题背景】如图1,点、分别在正方形的边、上, , 连接 , 我们可以通过把绕点逆时针旋转90°到 , 容易证得: .

 (1)、【迁移应用】如图2,四边形中, , , 点、分别在边、上, , 若、都不是直角,且 , 试探究、、之间的数量关系,并说明理由.(2)、【联系拓展】如图3,在中, , , 点、均在边BC上,且 . 猜想、、满足的等量关系(直接写出结论,不需要证明).22. 如图,一次函数与反比例函数的图象相交于点和点 .
(1)、【迁移应用】如图2,四边形中, , , 点、分别在边、上, , 若、都不是直角,且 , 试探究、、之间的数量关系,并说明理由.(2)、【联系拓展】如图3,在中, , , 点、均在边BC上,且 . 猜想、、满足的等量关系(直接写出结论,不需要证明).22. 如图,一次函数与反比例函数的图象相交于点和点 . (1)、求反比例函数的解析式;(2)、过点作轴于点 , 求;(3)、轴上是否存在一点 , 使得的值最小,若存在,求出点坐标;若不存在,请说明理由.
(1)、求反比例函数的解析式;(2)、过点作轴于点 , 求;(3)、轴上是否存在一点 , 使得的值最小,若存在,求出点坐标;若不存在,请说明理由.