山东省烟台市牟平区2022年中考一模数学试题
试卷更新日期:2023-03-31 类型:中考模拟
一、单选题
-
1. 下列实数中,有理数是( )A、 B、 C、 D、2. 下列是北京2022冬奥会的相关图案,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图1,已知 ,用尺规作它的角平分线.
3. 如图1,已知 ,用尺规作它的角平分线.如图2,步骤如下,
第一步:以B为圆心,以a为半径画弧,分别交射线 BA , BC 于点D,E;
第二步:分别以D,E为圆心,以b为半径画弧,两弧在 内部交于点P;
第三步:画射线 BP .射线 BP 即为所求.
下列正确的是( )
 A、a,b均无限制 B、 , 的长 C、a有最小限制,b无限制 D、 , 的长4. 据国家卫生健康委相关负责人介绍,截至2021年12月25日,31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗275809.4万剂次.数据“275809.4万”精确到千万位可用科学记数法表示为( )A、 B、 C、 D、5. 桌上摆着一个由若干个相同的小正方体组成的几何体,其主视图和左视图如图所示则组成这个几何体的小正方体的个数最多有( )
A、a,b均无限制 B、 , 的长 C、a有最小限制,b无限制 D、 , 的长4. 据国家卫生健康委相关负责人介绍,截至2021年12月25日,31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗275809.4万剂次.数据“275809.4万”精确到千万位可用科学记数法表示为( )A、 B、 C、 D、5. 桌上摆着一个由若干个相同的小正方体组成的几何体,其主视图和左视图如图所示则组成这个几何体的小正方体的个数最多有( ) A、10个 B、11个 C、12个 D、13个6. 已知一元二次方程的两个根分别为 , 则的值为( )A、-1 B、0 C、-2022 D、-20217. 下列关于运用计算器的说法错误的是( ).A、用计算器计算时,在按、、这三种键之前应先按键 B、要启动计算器的统计计算功能应按的键是 C、启动计算器的统计计算功能后,要清除原有统计数据应按键 D、用计算器计算时,依次按键显示结果是0.58. 关于x的分式方程的解为正数,且使关于y的一元一次不等式组有解,则所有满足条件的整数a的值之和是( )A、-5 B、-4 C、-3 D、-29. 下列说法错误的是( )A、从两名男生和两名女生中随机选两人当志愿者,则两人恰好是一男一女的概率是 . B、不透明袋子中装有除颜色外都一样的3个黑球和2个白球,从中任意摸出3个球,则摸出的3个球中至少有1个黑球是必然事件. C、若一组数据2、3、x、1、5的平均数是3,则这组数据的中位数是4,极差是4. D、如图是一张矩形纸板,连接各边中点得到菱形,再连接菱形各边中点得到一个小矩形.若从图中随机取点,则这个点取在阴影部分的概率是 .
A、10个 B、11个 C、12个 D、13个6. 已知一元二次方程的两个根分别为 , 则的值为( )A、-1 B、0 C、-2022 D、-20217. 下列关于运用计算器的说法错误的是( ).A、用计算器计算时,在按、、这三种键之前应先按键 B、要启动计算器的统计计算功能应按的键是 C、启动计算器的统计计算功能后,要清除原有统计数据应按键 D、用计算器计算时,依次按键显示结果是0.58. 关于x的分式方程的解为正数,且使关于y的一元一次不等式组有解,则所有满足条件的整数a的值之和是( )A、-5 B、-4 C、-3 D、-29. 下列说法错误的是( )A、从两名男生和两名女生中随机选两人当志愿者,则两人恰好是一男一女的概率是 . B、不透明袋子中装有除颜色外都一样的3个黑球和2个白球,从中任意摸出3个球,则摸出的3个球中至少有1个黑球是必然事件. C、若一组数据2、3、x、1、5的平均数是3,则这组数据的中位数是4,极差是4. D、如图是一张矩形纸板,连接各边中点得到菱形,再连接菱形各边中点得到一个小矩形.若从图中随机取点,则这个点取在阴影部分的概率是 . 10. 如图,在直角坐标系中,点A,B的坐标为A(0,2),B(﹣1,0),将△ABO绕点O按顺时针旋转得到△A1B1O,若AB⊥OB1 , 则点A1的坐标为( )
10. 如图,在直角坐标系中,点A,B的坐标为A(0,2),B(﹣1,0),将△ABO绕点O按顺时针旋转得到△A1B1O,若AB⊥OB1 , 则点A1的坐标为( )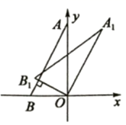 A、( ) B、( ) C、( ) D、( )11. 已知抛物线(a,b,c是常数), , 下列四个结论:
A、( ) B、( ) C、( ) D、( )11. 已知抛物线(a,b,c是常数), , 下列四个结论:①若抛物线经过点 , 则 . ②若 , 则方程一定有根 . ③抛物线与x轴一定有两个不同的公共点.④点在抛物线上,若 , 则当时, . 其中结论错误的个数是( )
A、1个 B、2个 C、3个 D、4个12. 如图,在平面直角坐标系中,点在直线上,过点作 , 交x轴于点;过点作轴,交直线l于点;过点作 , 交x轴于点;过点作轴,交直线l于点;…;按此作法进行下去,则点的坐标为( )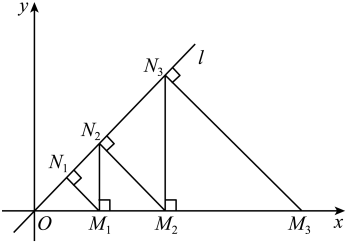 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
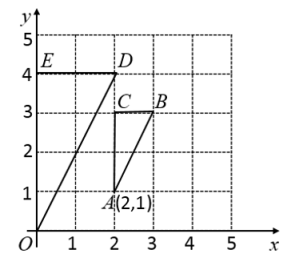
13. 若关于a代数式在实数范围内有意义,则实数a的取值范围是 .14. 如图,在直角坐标系中,与是位似图形,则位似中心的坐标为 .
 15. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图, 分别与 相切于点C,D,延长 交于点P.若 , 的半径为 ,则图中 的长为 .(结果保留 )
15. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图, 分别与 相切于点C,D,延长 交于点P.若 , 的半径为 ,则图中 的长为 .(结果保留 )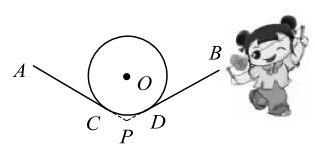 16. 如图,将三角形纸片 折叠,使点 、 都与点 重合,折痕分别为 、 .已知 , , ,则 的长为.
16. 如图,将三角形纸片 折叠,使点 、 都与点 重合,折痕分别为 、 .已知 , , ,则 的长为.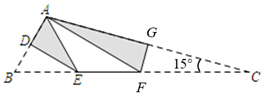 17. 一名高山滑雪运动员沿着斜坡滑行,他在点D处相对大树顶端A的仰角为 , 从D点再滑行米到达坡底的C点,在点C处相对树顶端A的仰角为 , 若斜坡的坡比为(点E,C,B在同一水平线上),则大树的高度米(结果保留根号).
17. 一名高山滑雪运动员沿着斜坡滑行,他在点D处相对大树顶端A的仰角为 , 从D点再滑行米到达坡底的C点,在点C处相对树顶端A的仰角为 , 若斜坡的坡比为(点E,C,B在同一水平线上),则大树的高度米(结果保留根号). 18. 如图,已知正方形 的边长为6,点F是正方形内一点,连接 ,且 ,点E是 边上一动点,连接 ,则 长度的最小值为 .
18. 如图,已知正方形 的边长为6,点F是正方形内一点,连接 ,且 ,点E是 边上一动点,连接 ,则 长度的最小值为 .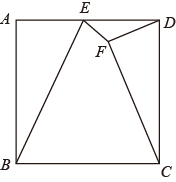
三、解答题
-
19. 先化简,再求值: ,其中m是已知两边分别为2和3的三角形的第三边长,且m是整数.20. 冰壶又被称作“冰上溜石”或“冰上国际象棋”,16世纪起源于苏格兰,当时是在冰上进行一种类似地滚球的游戏,直到1838年苏格兰冰上溜石俱乐部成立后才制定了正式的比赛规则.北京冬奥会前夕,北京某初级中学对1000名学生就“冰壶比赛规则”的了解程度进行了抽样调查(参与调查的同学只能选择其中一项),并将调查结果绘制出以下两幅不完整的统计图表,请根据统计图表回答下列问题:
类别
频数
频率
不了解
10
m
了解很少
16
0.32
基本了解
b
很了解
4
n
合计
a
1
 (1)、根据以上信息可知: , , , .(2)、补全条形统计图.(3)、估计该校1000名初中学生中“基本了解”的人数约有人.(4)、若“很了解”的4名学生是三男一女,现从这4人中随机抽取两人去参加北京市举办的“冰壶比赛规则”知识竞赛,请用画树状图或列表的方法说明,抽到两名学生均为男生和抽到一男一女的概率是否相同.21. 如图,点B是反比例函数y=(x>0)图象上一点,过点B分别向坐标轴作垂线,垂足为A,C.反比例函数y=(x>0)的图象经过OB的中点M,与AB,BC分别相交于点D,E.连接DE并延长交x轴于点F,点G与点O关于点C对称,连接BF,BG.
(1)、根据以上信息可知: , , , .(2)、补全条形统计图.(3)、估计该校1000名初中学生中“基本了解”的人数约有人.(4)、若“很了解”的4名学生是三男一女,现从这4人中随机抽取两人去参加北京市举办的“冰壶比赛规则”知识竞赛,请用画树状图或列表的方法说明,抽到两名学生均为男生和抽到一男一女的概率是否相同.21. 如图,点B是反比例函数y=(x>0)图象上一点,过点B分别向坐标轴作垂线,垂足为A,C.反比例函数y=(x>0)的图象经过OB的中点M,与AB,BC分别相交于点D,E.连接DE并延长交x轴于点F,点G与点O关于点C对称,连接BF,BG. (1)、填空:k=;(2)、求△BDF的面积;(3)、求证:四边形BDFG为平行四边形.22. “七一”建党节前夕,某校决定购买A,B两种奖品,用于表彰在“童心向党”活动中表现突出的学生.已知A奖品比B奖品每件多25元预算资金为1700元,其中800元购买A奖品,其余资金购买B奖品,且购买B奖品的数量是A奖品的3倍.(1)、求A,B奖品的单价;(2)、购买当日,正逢该店搞促销活动,所有商品均按原价八折销售,学校调整了购买方案:不超过预算资金且购买A奖品的资金不少于720元,A,B两种奖品共100件.求购买A,B两种奖品的数量,有哪几种方案?23. 图,在平行四边形中,是对角线, , 以点A为圆心,以的长为半径作 , 交边于点E,交于点F,连接 .
(1)、填空:k=;(2)、求△BDF的面积;(3)、求证:四边形BDFG为平行四边形.22. “七一”建党节前夕,某校决定购买A,B两种奖品,用于表彰在“童心向党”活动中表现突出的学生.已知A奖品比B奖品每件多25元预算资金为1700元,其中800元购买A奖品,其余资金购买B奖品,且购买B奖品的数量是A奖品的3倍.(1)、求A,B奖品的单价;(2)、购买当日,正逢该店搞促销活动,所有商品均按原价八折销售,学校调整了购买方案:不超过预算资金且购买A奖品的资金不少于720元,A,B两种奖品共100件.求购买A,B两种奖品的数量,有哪几种方案?23. 图,在平行四边形中,是对角线, , 以点A为圆心,以的长为半径作 , 交边于点E,交于点F,连接 . (1)、试判断直线与的位置关系,并证明你的判断.(2)、若 , , 求阴影部分的面积.24. 如图, 由 绕点 按逆时针方向旋转 得到,且点 的对应点D恰好落在 的延长线上, , 相交于点 .
(1)、试判断直线与的位置关系,并证明你的判断.(2)、若 , , 求阴影部分的面积.24. 如图, 由 绕点 按逆时针方向旋转 得到,且点 的对应点D恰好落在 的延长线上, , 相交于点 . (1)、求 的度数;(2)、 是 延长线上的点,且 .
(1)、求 的度数;(2)、 是 延长线上的点,且 .①判断 和 的数量关系,并证明;
②求证: .
25. 如图,在平面直角坐标系中,抛物线经过A(0,-1),B(4,1).直线AB交x轴于点C,P是直线AB下方抛物线上的一个动点.过点P作PD⊥AB,垂足为D,PE∥x轴,交AB于点E. (1)、求抛物线的函数表达式;(2)、当△PDE的周长取得最大值时,求点P的坐标和△PDE周长的最大值;(3)、把抛物线平移,使得新抛物线的顶点为(2)中求得的点P.M是新抛物线上一点,N是新抛物线对称轴上一点,直接写出所有使得以点A,B,M,N为顶点的四边形是平行四边形的点M的坐标,并把求其中一个点M的坐标的过程写出来.
(1)、求抛物线的函数表达式;(2)、当△PDE的周长取得最大值时,求点P的坐标和△PDE周长的最大值;(3)、把抛物线平移,使得新抛物线的顶点为(2)中求得的点P.M是新抛物线上一点,N是新抛物线对称轴上一点,直接写出所有使得以点A,B,M,N为顶点的四边形是平行四边形的点M的坐标,并把求其中一个点M的坐标的过程写出来.