山东省威海市2022年中考数学模拟试题

试卷更新日期：2023-03-31 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算下列各式，其结果为负数的是（）

A、 $- (- 3)$ B、 $| - 3 |$ C、 ${(- 3)}^{3}$ D、 ${(- 3)}^{2}$

查看试题解析
2. 如图是一个由6个相同的正方体组成的立体图形，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列说法正确的是（）

A、有两个内角相等的三角形不是轴对称图形 B、如果两条线段互相垂直平分，那么这两条线段互为对称轴 C、所有直角三角形都不是轴对称图形 D、两个图形成轴对称，那么这两个图形全等

查看试题解析
4. 在平面直角坐标系中，点M（﹣2，1）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 计算 $(a - \frac{1}{b}) \div (\frac{1}{a} - b)$ 的结果是（）

A、 $- \frac{a}{b}$ B、 $\frac{a}{b}$ C、 $- \frac{b}{a}$ D、 $\frac{b}{a}$

查看试题解析
6. 下列计算正确的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 $a^{6} \div a^{2} = a^{3}$ C、 $a \cdot a^{2} = a^{3}$ D、 ${(2 a^{2})}^{3} = 8 a^{5}$

查看试题解析
7. 若关于 $x$ 的方程 $x^{2} - 3 x + k = 0$ 有两个不相等的实数根，则 $k$ 的值不能是（）

A、2 B、0 C、 $\frac{9}{4}$ D、 $\sqrt{5}$

查看试题解析
8. 下列说法正确的是（）

A、三角形的外角一定大于它的内角 B、甲、乙两射击运动员分别射击10次，他们成绩的方差分别为 $S_{甲}^{2} = 4$ ， $S_{乙}^{2} = 9$ ，这过程中乙发挥比甲更稳定 C、8，9，10，11，11这组数的众数是2 D、两个图形位似也一定相似

查看试题解析
9. 某校举行春季运动会，需要在初一年级选取一名志愿者．初一（1）班、初一（2）班、初一（3）班各有2名同学报名参加．现从这6名同学中随机选取一名志愿者，则被选中的这名同学恰好是初一（3）班同学的概率是（　　）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
10. 如图， $R t Δ A B C$ 中， $∠ C = 90 °$ ，利用尺规在 $B C$ ， $B A$ 上分别截取 $B E$ ， $B D$ ，使 $B E = B D$ ；分别以D，E为圆心、以大于 $\frac{1}{2} D E$ 为长的半径作弧，两弧在 $∠ C B A$ 内交于点F；作射线 $B F$ 交 $A C$ 于点G，若 $C G = 1$ ，P为 $A B$ 上一动点，则 $G P$ 的最小值为（）

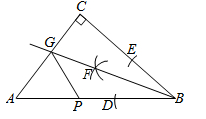A、无法确定 B、 $\frac{1}{2}$ C、1 D、2

查看试题解析

二、填空题

11. 如图，直线a∥b，正方形ABCD的顶点A、B分别在直线a、b上．若∠2＝73°，则∠1＝．

查看试题解析
12. 因式分解： $(m - 1)^{2} + 2 m - 2 =$ ．

查看试题解析
13. 若关于 $x$ 的一元二次方程 $(k - 2) x^{2} - 2 x + 1 = 0$ 有实数根，则 $k$ 的取值范围是．

查看试题解析
14. 一组数据1、3、 $x$ 、4、5的平均数是5，这组数据的中位数是．

查看试题解析
15. 设 $M = 2 x - 2$ ， $N = 3 x + 3$ ，若 $2 M - N = 2$ ，则x的值是.

查看试题解析
16. 算式 $3 - 7 + 8 - 6 + 13$ 按照性质符号读作为：．

查看试题解析

三、解答题

17. 解不等式组 ${\begin{array}{l} - 3 (x - 2) \geq 4 - x \\ \frac{2 x - 5}{3} < x - 1 \end{array}$ 并写出该不等式组的整数解．

查看试题解析
18. 激光电视的光源是激光，它运用反射成像原理，屏幕不通电无辐射，降低了对消费者眼睛的伤害．根据THX观影标准，当观影水平视场角“ $θ$ ”的度数处于 $33 °$ 到 $40 °$ 之间时（如图1），双眼肌肉处于放松状态，是最佳的感官体验的观影位．

(1)、小丽家决定要买一个激光电视，她家客厅的观影距离（人坐在沙发上眼睛到屏幕的距离）为3.5米，小佳家要选择电视屏幕宽（图2中的BC的长）在什么范围内的激光电视就能享受黄金观看体验？（结果精确到 $0.1 m$ ，参考数据： $s i n 33 ° \approx 0.54$ ， $t a n 33 ° \approx 0.65$ ， $s i n 40 ° \approx 0.64$ ， $t a n 40 ° \approx 0.84$ ， $s i n 16.5 ° \approx 0.28$ ， $t a n 16.5 ° \approx 0.30$ ， $s i n 20 ° \approx 0.34$ ， $t a n 20 ° \approx 0.36$ ）

(2)、由于技术革新和成本降低，激光电视的价格逐渐下降，某电器商行经营的某款激光电视今年每台销售价比去年降低4000元，在销售量相同的情况下，今年销售额在去年销售总额100万元的基础上减少 $20 %$ ，今年这款激光电视每台的售价是多少元？

查看试题解析
19. 某市举行知识大赛，A校、B校各派出5名选手组成代表队参加决赛，两校派出选手的决赛成绩如图所示．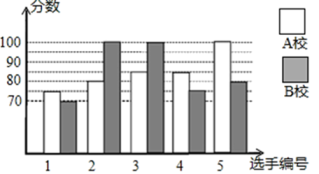

(1)、根据图示填写下表：

平均数/分

中位数/分

众数/分

A校

85

B校

85

100

(2)、结合两校成绩的平均数和中位数，分析哪个学校的决赛成绩较好；

(3)、计算两校决赛成绩的方差，并判断哪个学校代表队选手成绩较为稳定．

查看试题解析
20. 如图，四边形ABCD内接于⊙O，∠BAD＝90°，AD、BC的延长线交于点F，点E在CF上，且∠DEC＝∠BAC．

(1)、求证：DE是⊙O的切线；

(2)、当AB＝AC时，若CE＝4，EF＝6，求⊙O的半径．

查看试题解析
21. 我市某工艺厂设计了一款成本为20元/件的工艺品投放市场进行试销．经过调查，得到如表数据：
销售单价x（元/件）
…
30
40
50
60
…
每天销售量y（件）
…
500
400
300
200
…

(1)、上表中x、y的各组对应值满足一次函数关系，请求出y与x的函数关系式；

(2)、物价部门规定，该工艺品销售单价最高不能超过45元/件：
①销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？
②该工艺厂积极投入到慈善事业，它将该工艺品每件销售利润中抽取2元捐赠给我市的公共卫生事业，并且捐款后每天的利润不低于7600元，则工艺厂每天从这件工艺品的利润中最多可捐出多少元？

查看试题解析
22. 在如图的网格中建立平面直角坐标系， $△ A B C$ 的顶点坐标分别为 $A (1 ， 7)$ ， $B (5 ， 9)$ ， $C (6 ， 6)$ ，格点 $D (7 ， 1)$ ，只用无刻度的直尺在网格中完成下列画图，画图结果用实线表示，过程用虚线表示，并回答问题．
⑴作 $△ A B C$ 的中线 $A E$ ；
⑵在 $A B$ 上找一点 $P$ ，使得 $B P$ ： $A P = 2$ ： $3$ ；
⑶作点 $B$ 关于 $A C$ 的对称点 $F$ ；
⑷线段 $A C$ 和线段 $C D$ 存在一种特殊关系，即其中一条线段沿某条直线对折可以得到另一条线段，直接写出这条直线的解析式．

查看试题解析
23. 如图，在平面直角坐标系中，已知两点 $A (m ， 0)$ ， $B (0 ， n) (n > m > 0)$ ，点 $C$ 在第一象限， $A B ⊥ B C$ ， $B C = B A$ ，点 $P$ 在线段 $O B$ 上， $O P = O A$ ， $A P$ 的延长线与 $C B$ 的延长线交于点 $M$ ， $A B$ 与 $C P$ 交于点 $N$ ．

(1)、点 $C$ 的坐标为：（用含 $m$ ， $n$ 的式子表示）；

(2)、求证： $B M = B N$ ；

(3)、设点 $C$ 关于直线 $A B$ 的对称点为 $D$ ，点 $C$ 关于直线 $A P$ 的对称点为 $G$ ，求证： $D$ ， $G$ 关于 $x$ 轴对称．

查看试题解析
24. 如图，抛物线y=kx²-2kx-3k交x轴于A、B两点，交y轴于点C，已知OC=OB．

(1)、求抛物线解析式；

(2)、在直线BC上求点P，使PA+PO的值最小；

(3)、抛物线上是否存在点Q，使△QBC的面积等于6？若存在，请求出Q的坐标；若不存在请说明理由．

查看试题解析

销售单价x（元/件）	…	30	40	50	60	…
每天销售量y（件）	…	500	400	300	200	…

	平均数/分	中位数/分	众数/分
A校		85
B校	85		100