山东省泰安市2022年中考数学一模试题
试卷更新日期:2023-03-31 类型:中考模拟
一、单选题
-
1. 如图所示的几何体是由 个大小相同的小立方块搭成,它的左视图是( )
 A、
A、 B、
B、 C、
C、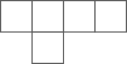 D、
D、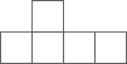 2. 原子钟是以原子的规则振动为基础的各种守时装置的统称,其中氢脉泽钟的精度达到了1700000年误差不超过1秒.数据1700000用科学记数法表示( )A、 B、 C、 D、3. 如图, , 是 的外角, ,则 的大小是( )
2. 原子钟是以原子的规则振动为基础的各种守时装置的统称,其中氢脉泽钟的精度达到了1700000年误差不超过1秒.数据1700000用科学记数法表示( )A、 B、 C、 D、3. 如图, , 是 的外角, ,则 的大小是( )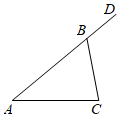 A、 B、 C、 D、4. 已知某快递公司的收费标准为:寄一件物品不超过5千克,收费13元;超过5千克的部分每千克加收2元.圆圆在该快递公司寄一件8千克的物品,需要付费( )A、17元 B、19元 C、21元 D、23元5. 下列运算正确的是( )A、x2+x2=x4 B、(a-b)2=a2-b2 C、(-a2)3=-a6 D、6. 山茶花是温州市的市花、品种多样,“金心大红”是其中的一种,某兴趣小组对30株“金心大红”的花径进行测量、记录,统计如下表。
A、 B、 C、 D、4. 已知某快递公司的收费标准为:寄一件物品不超过5千克,收费13元;超过5千克的部分每千克加收2元.圆圆在该快递公司寄一件8千克的物品,需要付费( )A、17元 B、19元 C、21元 D、23元5. 下列运算正确的是( )A、x2+x2=x4 B、(a-b)2=a2-b2 C、(-a2)3=-a6 D、6. 山茶花是温州市的市花、品种多样,“金心大红”是其中的一种,某兴趣小组对30株“金心大红”的花径进行测量、记录,统计如下表。株数(株)
7
9
12
2
花径(cm)
6.5
6.6
6.7
6.8
这批“金心大红”花径的众数为( )
A、6.5cm B、6.6cm C、6.7cm D、6.8cm7. 从下列4个函数:①y=3x-2;②y=(x<0);③y=(x>0);④y=-x2(x<0)中任取一个,函数值y随自变量x的增大而增大的概率是( )A、 B、 C、 D、18. 如图,A、B是双曲线上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为( )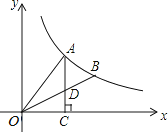 A、 B、 C、3 D、49. 如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )
A、 B、 C、3 D、49. 如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )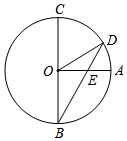 A、3α+β=180° B、2α+β=180° C、3α﹣β=90° D、2α﹣β=90°10. 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE+DF=AF+DE.其中正确的是( )
A、3α+β=180° B、2α+β=180° C、3α﹣β=90° D、2α﹣β=90°10. 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE+DF=AF+DE.其中正确的是( )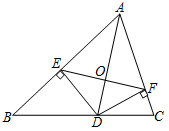 A、②③ B、②④ C、①③④ D、②③④11. 在平面直角坐标系中,已知函数 , , , 其中a,b,c是正实数,且满足 . 设函数 , , 的图象与x轴的交点个数分别为 , , , 则下列说法一定正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则12. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m, ),反比例函数 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
A、②③ B、②④ C、①③④ D、②③④11. 在平面直角坐标系中,已知函数 , , , 其中a,b,c是正实数,且满足 . 设函数 , , 的图象与x轴的交点个数分别为 , , , 则下列说法一定正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则12. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m, ),反比例函数 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )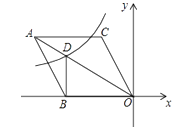 A、 B、- C、 D、-
A、 B、- C、 D、-二、填空题
-
13. 如图,AB∥CD,EF分别与AB,CD交于点B,F,若∠E=30°,∠EFC=130°,则∠A=。
 14. 如图,已知AB是⊙O的直径,BC与⊙O相切于点B,连接AC,OC.若sin∠BAC= ,则tan∠BOC= .
14. 如图,已知AB是⊙O的直径,BC与⊙O相切于点B,连接AC,OC.若sin∠BAC= ,则tan∠BOC= .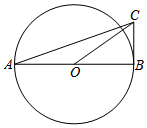 15. 计算: .16. 如图,在平面直角坐标系中,正比例函数y=kx与反比例函数 的图象交于A,B两点,过A作y轴的垂线,交反比例函数 (x>0)的图象于点C,连接BC,若S△ABC=8,则k的值为.
15. 计算: .16. 如图,在平面直角坐标系中,正比例函数y=kx与反比例函数 的图象交于A,B两点,过A作y轴的垂线,交反比例函数 (x>0)的图象于点C,连接BC,若S△ABC=8,则k的值为.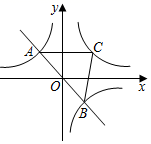 17. 如图,已知一次函数 与反比例函数 的图象相交于点P,则关于x的方程 的解是 .
17. 如图,已知一次函数 与反比例函数 的图象相交于点P,则关于x的方程 的解是 . 18. 如图,在矩形ABCD中,AB=6,BC=10,以点B为圆心、BC的长为半径画弧交AD于点E , 再分别以点C , E为圆心、大于 CE的长为半径画弧,两弧交于点F , 作射线BF交CD于点G , 则CG的长为 .
18. 如图,在矩形ABCD中,AB=6,BC=10,以点B为圆心、BC的长为半径画弧交AD于点E , 再分别以点C , E为圆心、大于 CE的长为半径画弧,两弧交于点F , 作射线BF交CD于点G , 则CG的长为 .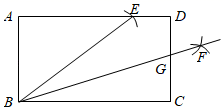
三、解答题
-
19. 计算(1)、先化简,再求值: , 其中 .(2)、解不等式组:20. 如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.
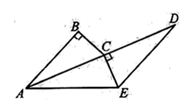 (1)、求证:△ABC≌△DCE;(2)、连结AE,当BC=5,AC=12时,求AE的长.21. 如图,CD= CA,∠1 = ∠2,EC=BC.
(1)、求证:△ABC≌△DCE;(2)、连结AE,当BC=5,AC=12时,求AE的长.21. 如图,CD= CA,∠1 = ∠2,EC=BC.求证:DE=AB.
 22. 某校的甲、乙两位老师同住一小区,该小区与学校相距2400米. 甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校义骑行若干米到达还车点后,立即步行走回学校. 已知甲步行的速度比乙步行的速度每分钟快5米. 设甲步行的时间为(分),图1中线段和折线分别表示甲、乙离开小区的路程(米)与甲步行时间(分)的函数关系的图象;图2表示甲、乙两人之间的距离(米)与甲步行时间(分)的函数关系的图象(不完整).
22. 某校的甲、乙两位老师同住一小区,该小区与学校相距2400米. 甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校义骑行若干米到达还车点后,立即步行走回学校. 已知甲步行的速度比乙步行的速度每分钟快5米. 设甲步行的时间为(分),图1中线段和折线分别表示甲、乙离开小区的路程(米)与甲步行时间(分)的函数关系的图象;图2表示甲、乙两人之间的距离(米)与甲步行时间(分)的函数关系的图象(不完整).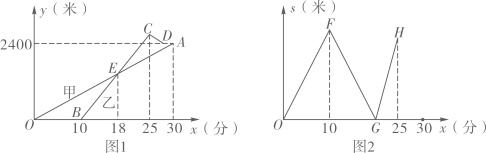
根据图1和图2中所给信息,解答下列问题:
(1)、求甲步行的速度和乙出发时甲离开小区的路程;(2)、求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;(3)、在图2中,画出当时关于的函数的大致图象. (温馨提示:请画在答题卷相对应的图上)23. 在平面直角坐标系中,设二次函数y1=x2+bx+a , y2=ax2+bx+1(a , b是实数,a≠0).(1)、若函数y1的对称轴为直线x=3,且函数y1的图象经过点(a , b),求函数y1的表达式.(2)、若函数y1的图象经过点(r , 0),其中r≠0,求证:函数y2的图象经过点( ,0).(3)、设函数y1和函数y2的最小值分别为m和n , 若m+n=0,求m , n的值.24. 如图,已知AC,BD为⊙O的两条直径,连接AB,BC,OE⊥AB于点E,点F是半径OC的中点,连接EF.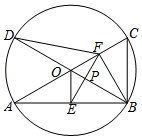 (1)、设⊙O的半径为1,若∠BAC=30°,求线段EF的长.(2)、连接BF,DF,设OB与EF交于点P,
(1)、设⊙O的半径为1,若∠BAC=30°,求线段EF的长.(2)、连接BF,DF,设OB与EF交于点P,①求证:PE=PF.
②若DF=EF,求∠BAC的度数.
25. 如图1,在平面直角坐标系中,直线y= x+1分别与x轴、y轴交于点A , C , 经过点C的抛物线y= x2+bx+c与直线y= x+1的另一个交点为点D , 点D的横坐标为6.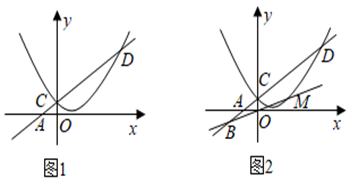 (1)、求抛物线的表达式.(2)、M为抛物线上的动点.
(1)、求抛物线的表达式.(2)、M为抛物线上的动点.①N为x轴上一点,当四边形CDMN为平行四边形时,求点M的坐标;
②如图2,点M在直线CD下方,直线OM(OM∥CD的情况除外)交直线CD于点B , 作直线BD关于直线OM对称的直线B ,当直线B 与坐标轴平行时,直接写出点M的横坐标.