山东省泰安市高新区2022年中考数学模拟试题

试卷更新日期：2023-03-31 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列说法正确的是（　　）

A、带正号的数是正数，带负号的数是负数 B、一个数的相反数，不是正数，就是负数 C、倒数等于本身的数有2个 D、零除以任何数等于零

查看试题解析
2. 下列图形中，是中心对称图形的是（）

A、正三角形 B、圆 C、正五边形 D、等腰梯形

查看试题解析
3. 2018年，全国教育经费投入为46135亿元，比上年增长 $8.39 %$ 。其中，国家财政性教育经费（主要包括一般公共预算安排的教育经费，政府性基金预算安排的教育经费，企业办学中的企业拨款，校办产业和社会服务收入用于教育的经费等）为36990亿元，约占国内生产总值的 $4.11 %$ 。其中36990亿用科学记数法表示为（）

A、 $0.3699 \times 10^{13}$ B、 $3.699 \times 10^{12}$ C、 $3.699 \times 10^{13}$ D、 $36.99 \times 10^{11}$

查看试题解析
4. 方程 $2 x^{2} - k x - 1 = 0$ 的根的情况是（）

A、方程有两个相等的实数根 B、方程有两个不相等的实数根 C、方程没有实数根 D、方程的根的情况与 $k$ 的取值有关

查看试题解析
5. 最近央视纪录片《航拍中国》中各地的美景震撼了全国观众，如图是航拍无人机从A点俯拍在坡比为3：4的斜坡CD上的景点C，此时的俯角为30°，为取得更震撼的拍摄效果，无人机升高200米到达B点，此时的俯角变为45°．已知无人机与斜坡CD的坡底D的水平距离DE为400米，则斜坡CD的长度为（）米（精确到0.1米，参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）

A、91.1 B、91.3 C、58.2 D、58.4

查看试题解析
6. 对于抛物线 $y = - 2 (x - 1)^{2} + 3$ ，下列判断正确的是（）

A、顶点 $(- 1 ， 3)$ B、抛物线向左平移 $3$ 个单位长度后得到 $y = - 2 (x - 2)^{2} + 3$ C、抛物线与y轴的交点是 $(0 ， 1)$ D、当 $x > 1$ 时，y随x的增大而增大

查看试题解析
7. 已知 $a = 2^{44}$ ， $b = 3^{33}$ ， $c = 5^{22}$ ，那么 $a$ 、 $b$ 、 $c$ 的大小关系是（）

A、 $a > b > c$ B、 $a < b < c$ C、 $c > a > b$ D、 $b > c > a$

查看试题解析
8. 如图，把一张长方形的纸片ABCD沿EF折叠，若∠AED'＝40°，则∠EFB的度数为（）

A、40° B、50° C、60° D、70°

查看试题解析
9. 下列说法正确的是（　　）

A、九年级某班的英语测试平均成绩是98.5，说明每个同学的得分都是98.5分 B、数据4，4，5，5，0的中位数和众数都是5 C、要了解一批日光灯的使用寿命，应采用全面调查 D、若甲、乙两组数据中各有20个数据，两组数据的平均数相等，方差S_甲²＝1.25，S_乙²＝0.96，则说明乙组数数据比甲组数据稳定

查看试题解析
10. 如图，AB是⊙O直径，若∠AOC＝150°，则∠D的度数是（）

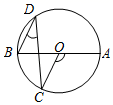A、15° B、25° C、30° D、75°

查看试题解析
11. 如图，等边△ABC中，AB=2，D为△ABC内一点，且DA=DB，E为△ABC外一点，BE=AB，且∠EBD=∠CBD，连接DE，CE，则下列结论：①∠DAC=∠DBC；②BE⊥AC；③∠DEB=30°；④若EC∥AD，则S_△_EBC=1，其中正确的有（）

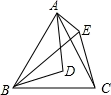A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 如图，在边长为 $1$ 的正方形 $A B C D$ 中，动点 $F$ ， $E$ 分别以相同的速度从 $D$ ， $C$ 两点同时出发向 $C$ 和 $B$ 运动 $($ 任何一个点到达即停止 $)$ ，连接 $A E$ 、 $B F$ 交于点 $P$ ，过点 $P$ 作 $P M ∥ C D$ 交 $B C$ 于 $M$ 点， $P N ∥ B C$ 交 $C D$ 于 $N$ 点，连接 $M N$ ，在运动过程中则下列结论：① $△ A B E ≌ △ B C F$ ；② $A E = B F$ ；③ $A E ⊥ B F$ ；④ $C F^{2} = P E \cdot B F$ ；⑤线段 $M N$ 的最小值为 $\frac{\sqrt{5} - 1}{2}$ ．
其中正确的结论有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

13. 如图，一张宽为 $3$ ，长为 $4$ 的矩形纸片 $A B C D$ ，先沿对角线 $B D$ 对折，点 $C$ 落在 $C^{'}$ 的位置， $B C^{'}$ 交 $A D$ 于 $G$ ，再折叠一次，使点 $D$ 与点 $A$ 重合，得折痕 $E N$ ， $E N$ 交 $A D$ 于 $M$ ，则 $M E =$ ．

查看试题解析
14. 如图，在菱形 $A B C D$ 中， $A B = 5$ ， $A C = 8$ ，点 $M$ ， $N$ 在 $A C$ 上，且 $M N = 1$ ，连接 $B M$ ， $D N$ ，则 $B M + D N$ 的最小值为．

查看试题解析
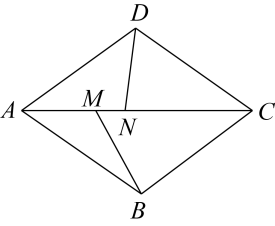15. 我国古代数学的许多成就都曾位居世界前列，其中“杨辉三角”就是一例，例如，在三角形中第三行的三个数1，2，1，恰好对应 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ 展开式中的系数；第四行的四个数1，3，3，1，恰好对应着 ${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{3} + b^{3}$ 展开式中的系数； $\dots \dots$ 请根据规律直接写出 ${(a + 6)}^{4}$ 的展开式．

查看试题解析
16. 如图，点 $P (2 ， 4)$ 绕点 $O$ 旋转 $90 °$ 得到点 $P^{'}$ ，则点 $P^{'}$ 的坐标是．

查看试题解析
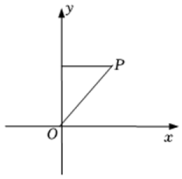17. 如图，在△ABC中，BC=6，以点A为圆心，2为半径的☉A与BC相切于点D，交AB于点E，交AC于点F，点P是优弧 $\overset{⌢}{EF}$ 上的一点，且∠EPF=50°，则图中阴影部分的面积是.

查看试题解析
18. 若关于 $x$ 的不等式组 ${\begin{array}{l} \frac{2 x + 3}{3} \geq x - 1 \\ 6 x - 6 > a - 4 \end{array}$ 有且只有五个整数解，且关于 $y$ 的分式方程 $\frac{3 y}{y - 2} - \frac{a - 10}{2 - y} = 1$ 的解为非负整数，则符合条件的所有整数 $a$ 的和为．

查看试题解析

三、解答题

19. 汽车油箱中的余油量 $Q$ （升 $)$ 是它行驶的时间 $t$ （小时）的一次函数.某天该汽车外出时，油箱中余油量与行驶时间的变化关系如图：

(1)、根据图象，求油箱中的余油 $Q$ 与行驶时间 $t$ 的函数关系.

(2)、从开始算起，如果汽车每小时行驶40千米，当油箱中余油20升时，该汽车行驶了多少千米？

查看试题解析
20. 先化简，再求值：（ $\frac{2}{m - 1}$ ﹣1）÷ $\frac{m^{2} - 3 m}{m^{2} - 1}$ ，其中m＝ $\sqrt{2}$ .

查看试题解析
21. 如图，直线l₁：y＝kx+b与双曲线y＝ $\frac{m}{x}$ （x＞0）交于A，B两点，与x轴交于点C，与y轴交于点E，已知点A（1，3），点C（4，0）．

(1)、求直线l₁和双曲线的解析式；

(2)、将△OCE沿直线l₁翻折，点O落在第一象限内的点H处，求点H的坐标；

(3)、如图，过点E作直线l₂：y＝3x+4交x轴的负半轴于点F，在直线l₂上是否存在点P，使得S_△PBC＝S_△OBC？若存在，请直接写出所有符合条件的点P的坐标；如果不存在，请说明理由．

查看试题解析
22. 如图，在 $△ ABC$ 中， $A B = A C$ ，点E在边BC上移动（点E不与点B、C重合），满足 $∠ DEF = ∠ B$ ，且点D、F分别在边AB、AC上．

(1)、求证： $△ B D E \sim △ C E F$ ；

(2)、当点E移动到BC的中点时，求证：FE平分 $∠ DFC$ ．

查看试题解析
23. 亚健康是时下社会热门话题，进行体育锻炼是远离亚健康的一种重要方式，为了解某校八年级学生每天进行体育锻炼的时间情况，随机抽样调查了100名初中学生，根据调查结果得到如图所示的统计图表．
类别
时间t（小时）
人数
A
t≤0.5
5
B
0.5＜t≤1
20
C
1＜t≤1.5
a
D
1.5＜t≤2
30
E
t＞2
10
请根据图表信息解答下列问题：

(1)、a=；

(2)、补全条形统计图；

(3)、小王说：“我每天的锻炼时间是调查所得数据的中位数”，问小王每天进行体育锻炼的时间在什么范围内？

(4)、若把每天进行体育锻炼的时间在1小时以上定为锻炼达标，则被抽查学生的达标率是多少？

查看试题解析
24. 如图（1）AC⊥AB，BD⊥AB，AB＝12cm，AC＝BD＝8cm，点P在线段AB上以2cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动，它们运动的时间为t（s）.

(1)、若点Q的运动速度与点P的运动速度相等，当t＝2时，△ACP与△BPQ是否全等，请说明理由；

(2)、在（1）的条件下，判断此时线段PC和线段PQ的位置关系，并证明；

(3)、如图（2），将图（1）中的“AC⊥AB，BD⊥AB”改为“∠CAB＝∠DBA＝50°”，其他条件不变.设点Q的运动速度为xcm/s，是否存在实数x，使得△ACP与△BPQ全等？若存在，求出相应的x、t的值；若不存在，请说明理由.

查看试题解析
25. 如图，抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴交于点 $A$ 、 $B$ （ $A$ 与 $B$ 的左侧），交 $y$ 轴的负半轴于点 $C$ ， $O C = 3 O B$ ， $B$ 点的坐标为 $(1 ， 0)$ ．

(1)、求抛物线的解析式；

(2)、点 $D$ 是抛物线对称轴与 $x$ 轴的交点，点 $P$ 是第三象限内抛物线上一点，当 $△ P C D$ 面积最大时，求点 $P$ 的坐标；

(3)、在（2）的结论下，绕点 $D$ 旋转直线 $C D$ 得到直线 $l$ ，当直线 $l$ 经过点 $P$ 时停止旋转，在旋转过程中，直线 $l$ 与线段 $C P$ 交于点 $N$ ，设点 $C$ ， $P$ 到直线 $l$ 的距离分别为 $d_{1}$ ， $d_{2}$ ，当 $d_{1} + d_{2}$ 最大时，求直线 $l$ 旋转的角度．

查看试题解析

类别	时间t（小时）	人数
A	t≤0.5	5
B	0.5＜t≤1	20
C	1＜t≤1.5	a
D	1.5＜t≤2	30
E	t＞2	10