山东省泰安市东平县2022年中考数学一模试题
试卷更新日期:2023-03-31 类型:中考模拟
一、单选题
-
1. 在0,2,-2,-3.5这四个数中,是负整数的是( )A、0 B、2 C、-2 D、-3.52. 下列计算结果正确的是( )A、 B、 C、 D、3. 下图是某个几何体的三视图,该几何体是( )
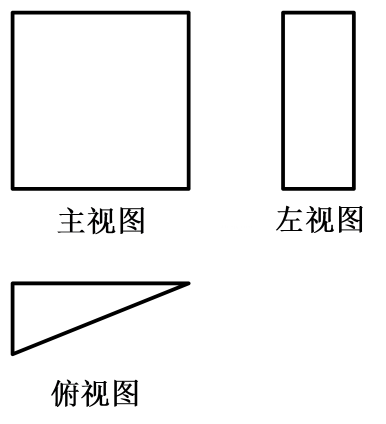 A、长方体 B、正方体 C、圆柱 D、三棱柱4. 如图,已知直线AC//BD,BF与AC交于点F,若∠A=23°,∠AEB=58°,则∠B=( )
A、长方体 B、正方体 C、圆柱 D、三棱柱4. 如图,已知直线AC//BD,BF与AC交于点F,若∠A=23°,∠AEB=58°,则∠B=( ) A、23° B、58° C、35° D、45°5. 八年级(1)班30名学生的身高情况如下表:
A、23° B、58° C、35° D、45°5. 八年级(1)班30名学生的身高情况如下表:身高(m)
1.45
1.48
1.50
1.53
1.55
1.65
1.70
人数
X
y
6
8
5
3
1
关于身高的统计量中,不随x、y的变化而变化的有( )
A、众数,中位数 B、中位数,方差 C、平均数,方差 D、平均数,众数6. 如图,是的直径,点是外一点,交于点 , 连接 , 若 ,且与相切,则此时等于( ) A、 B、 C、 D、7. 关于的一元二次方程有两个相等的实数根,则的值为( )A、1 B、-1 C、3或-1 D、-38. 抛物线y=x2+1经过平移得到抛物线y=(x-6)2+4,平移过程正确的是( )A、先向左平移6个单位,再向上平移3个单位 B、先向左平移6个单位,再向下平移3个单位 C、先向右平移6个单位,再向上平移3个单位 D、先向右平移6个单位,再向下平移3个单位9. 如图,四边形ABCD是⊙O的内接四边形,若∠C=100°,则∠BOD的度数是( )
A、 B、 C、 D、7. 关于的一元二次方程有两个相等的实数根,则的值为( )A、1 B、-1 C、3或-1 D、-38. 抛物线y=x2+1经过平移得到抛物线y=(x-6)2+4,平移过程正确的是( )A、先向左平移6个单位,再向上平移3个单位 B、先向左平移6个单位,再向下平移3个单位 C、先向右平移6个单位,再向上平移3个单位 D、先向右平移6个单位,再向下平移3个单位9. 如图,四边形ABCD是⊙O的内接四边形,若∠C=100°,则∠BOD的度数是( ) A、100° B、120° C、130° D、160°10. 如图,将▱DEBF的对角线EF向两端延长,分别至点A和点C,且使AE=CF,连接AB,BC,AD,CD.求证:四边形ABCD为平行四边形.
A、100° B、120° C、130° D、160°10. 如图,将▱DEBF的对角线EF向两端延长,分别至点A和点C,且使AE=CF,连接AB,BC,AD,CD.求证:四边形ABCD为平行四边形.以下是证明过程,其顺序已被打乱,
①∴四边形ABCD为平行四边形;②∵四边形DEBF为平行四边形,∴OD=OB,OE=OF;③连接BD,交AC于点O;④又∵AE=CF,∴AE+OE=CF+OF,即OA=OC
正确的证明步骤是( )
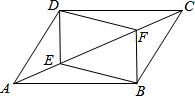 A、①②③④ B、③④②① C、③②④① D、④③②①11. 如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长 米,背水坡CD的坡度 ,则背水坡的坡长CD为( )米.
A、①②③④ B、③④②① C、③②④① D、④③②①11. 如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长 米,背水坡CD的坡度 ,则背水坡的坡长CD为( )米.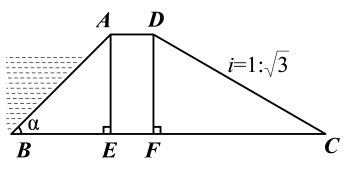 A、20 B、 C、10 D、12. 如图,在矩形ABCD中,E、F分别在BC、CD上运动(不与端点重合),连接BF、AE,交于点P,且满足 . 连接CP,若AB=4,BC=6,则CP的最小值为 ( )
A、20 B、 C、10 D、12. 如图,在矩形ABCD中,E、F分别在BC、CD上运动(不与端点重合),连接BF、AE,交于点P,且满足 . 连接CP,若AB=4,BC=6,则CP的最小值为 ( )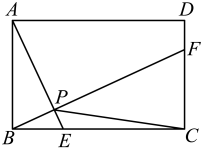 A、2-3 B、2-2 C、5 D、3
A、2-3 B、2-2 C、5 D、3二、填空题
-
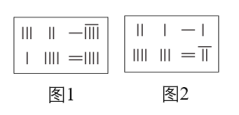
13. 纳米是一种长度单位,纳米米,冠状病毒的直径为纳米,用科学记数法表示为米.14. 在《九章算术》中,二元一次方程组是通过“算筹”摆放的.若图中各行从左到右列出的三组算筹分别表示未知数 , 的系数与相应的常数项,如图1表示方程组是 , 则如图2表示的方程组是 .
 15. 已知抛物线y=ax2+bx+c如图所示,它与x轴的两交点的横坐标分别是-1,5.对于下列结论:①abc>0;②方程ax2+bx+c=0的根是x1=-1,x2=5;③9a-3b+c<0;④当x<2时,y随着x的增大而增大.
15. 已知抛物线y=ax2+bx+c如图所示,它与x轴的两交点的横坐标分别是-1,5.对于下列结论:①abc>0;②方程ax2+bx+c=0的根是x1=-1,x2=5;③9a-3b+c<0;④当x<2时,y随着x的增大而增大.其中正确的结论是(填写结论的序号).
 16. 如图,在中, , 分别以、、边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”.当 , 时,则阴影部分的面积为 .
16. 如图,在中, , 分别以、、边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”.当 , 时,则阴影部分的面积为 . 17. 如图,在平面直角坐标系中,点A,B,C的坐标分别为(8,0),(8,6), , 点D为线段上一动点,将沿翻折,使点C落到点E处.当B,E两点之间距离最短时,点D的坐标为 .
17. 如图,在平面直角坐标系中,点A,B,C的坐标分别为(8,0),(8,6), , 点D为线段上一动点,将沿翻折,使点C落到点E处.当B,E两点之间距离最短时,点D的坐标为 . 18. 如图,已知等边 , 是边的中点,过作DEAB于 , 连接交于;过作D1E1AB于 , 连接交于;过作D2E2AB于 , , 如此继续,若记为 , 记为 , 记为 , 若面积为cm2 , 则 cm2用含与的代数式表示
18. 如图,已知等边 , 是边的中点,过作DEAB于 , 连接交于;过作D1E1AB于 , 连接交于;过作D2E2AB于 , , 如此继续,若记为 , 记为 , 记为 , 若面积为cm2 , 则 cm2用含与的代数式表示
三、解答题
-
19. 计算(1)、先化简,再求值: , 其中 .(2)、解不等式: .20. 青年大学习由共青团中央发起,广大青年参与,通过学习来提升自身理论水平、思维层次的行动,梦想从学习开始,事业从实践起步.某校为了解九年级同学学习“青年大学习”的情况,随机抽取部分九年级同学进行了问卷调查,按照调查结果,将学习情况分为优秀、良好、合格、较差四个等级.学校绘制了如图不完整的统计图,根据图中信息解答下列问题:
 (1)、本次参与问卷调查的初中生共为 ▲ 人;将条形统计图补充完整;(2)、扇形统计图中“合格”所对应的百分比为 , “较差”所对应的圆心角度数为度;(3)、该校某班有4名同学(2名男同学、2名女同学)在调查中获得“优秀”等级,班主任将从这4名同学中随机选取2名同学,代表班级参加学校组织的“青年大学习”演讲大赛.请用列表或画树状图的方法,求所选两位同学恰好是1名男同学和1名女同学的概率.21. 如图,一次函数 的图象与 轴交于点 ,与 轴交于点 ,与反比例函数 的图象交于B,D两点,且AC=BC.
(1)、本次参与问卷调查的初中生共为 ▲ 人;将条形统计图补充完整;(2)、扇形统计图中“合格”所对应的百分比为 , “较差”所对应的圆心角度数为度;(3)、该校某班有4名同学(2名男同学、2名女同学)在调查中获得“优秀”等级,班主任将从这4名同学中随机选取2名同学,代表班级参加学校组织的“青年大学习”演讲大赛.请用列表或画树状图的方法,求所选两位同学恰好是1名男同学和1名女同学的概率.21. 如图,一次函数 的图象与 轴交于点 ,与 轴交于点 ,与反比例函数 的图象交于B,D两点,且AC=BC.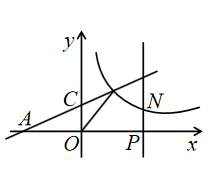 (1)、求反比例函数的解析式;(2)、已知 是 轴正半轴上一点,作 轴交直线 于点 ,交双曲线于点 ,当 , , , 为顶点的四边形为平行四边形时,请写出点 的坐标.22. 某校在商场购进A、B两种品牌的篮球,购买A品牌篮球花费了2500元,购买B品牌篮球花费了2000元,且购买A品牌篮球的数量是购买B品牌篮球数量的2倍,已知购买一个B品牌篮球比购买一个A品牌篮球多花30元.(1)、问购买一个A品牌、一个B品牌的篮球各需多少元?(2)、该校决定再次购进A、B两种品牌篮球共50个,恰逢商场对两种品牌篮球的售价进行调整,A品牌篮球售价比第一次购买时提高了8%,B品牌篮球按第一次购买时售价的9折出售,如果该校此次购买A、B两种品牌篮球的总费用不超过3060元,那么该校此次最多可购买多少个B品牌篮球?23. 在中, , , 于点 .
(1)、求反比例函数的解析式;(2)、已知 是 轴正半轴上一点,作 轴交直线 于点 ,交双曲线于点 ,当 , , , 为顶点的四边形为平行四边形时,请写出点 的坐标.22. 某校在商场购进A、B两种品牌的篮球,购买A品牌篮球花费了2500元,购买B品牌篮球花费了2000元,且购买A品牌篮球的数量是购买B品牌篮球数量的2倍,已知购买一个B品牌篮球比购买一个A品牌篮球多花30元.(1)、问购买一个A品牌、一个B品牌的篮球各需多少元?(2)、该校决定再次购进A、B两种品牌篮球共50个,恰逢商场对两种品牌篮球的售价进行调整,A品牌篮球售价比第一次购买时提高了8%,B品牌篮球按第一次购买时售价的9折出售,如果该校此次购买A、B两种品牌篮球的总费用不超过3060元,那么该校此次最多可购买多少个B品牌篮球?23. 在中, , , 于点 . (1)、如图所示,点 , 分别在线段 , 上,且 , 当 , 时,求线段的长;(2)、如图所示,点 , 分别在 , 上,且 , 求证:是等腰直角三角形;(3)、如图所示,点在的延长线上,点在上,且 , 求证: .
(1)、如图所示,点 , 分别在线段 , 上,且 , 当 , 时,求线段的长;(2)、如图所示,点 , 分别在 , 上,且 , 求证:是等腰直角三角形;(3)、如图所示,点在的延长线上,点在上,且 , 求证: .

