山东省泰安市岱岳区2022年中考数学模拟试卷

试卷更新日期：2023-03-31 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列式子：① ${(- 7)}^{- 2} = \frac{1}{49}$ ；② $a^{0} = 1$ ；③ $3 a^{- 2} = \frac{1}{3 a^{2}}$ ；④ $- 7.02 \times 1 0^{- 4} = - 0.000702$ ，其中正确的式子有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 如图，现将一块三角板的含有60°角的顶点放在直尺的一边上，若∠1=2∠2，那么∠1的度数为（）

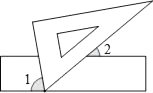A、50° B、60° C、70° D、80°

查看试题解析
3. 甲、乙两组各有12名学生，组长绘制了本组最近网上学习平均一天所需时间的统计图表如下，比较两组网上学习平均一天所需时间的中位数，下列说法正确的是（）
甲组12名学生网上学习平均一天所需的统计表
平均一天所需时间 $(h)$
5
6
7
9
学生数
4
5
2
1
乙组12名同学网上学习平均一天所需时间统计图

A、甲组比乙组大 B、乙组比甲组大 C、甲乙两组相同 D、无法判断

查看试题解析
4. 如图，四边形ABCD为 $⊙ O$ 的内接四边形， $∠ B C D = 132 °$ ，则 $∠ B O D$ 的度数为（）

A、48° B、96° C、132° D、144°

查看试题解析
5. 为测量此塔顶 $B$ 的高度，在地面选取了与塔底 $D$ 共线的两点 $A$ 、 $C$ ， $A$ 、 $C$ 在 $D$ 的同侧，在 $A$ 处测量塔顶 $B$ 的仰角为 $27 °$ ，在 $C$ 处测量塔顶 $B$ 的仰角为 $45 °$ ， $A$ 到 $C$ 的距离是89.5米．设 $B D$ 的长为 $x$ 米，则下列关系式正确的是（）

A、 $t a n 27 ° = \frac{x}{x + 89.5}$ B、 $c o s 27 ° = \frac{x}{x + 89.5}$ C、 $s i n 27 ° = \frac{x}{x + 89.5}$ D、 $t a n 27 ° = \frac{x + 89.5}{x}$

查看试题解析
6. 不等式 $x + 3 > \frac{1}{2}$ 的负整数解有（）个

A、1 B、2 C、3 D、4

查看试题解析
7. 将二次函数 $y = {(x - 1)}^{2}$ 的图象向上平移2个单位长度，再向左平移3个单位长度，得到抛物线 $y = x^{2} + b x + c$ ，则 $b$ ， $c$ 的值分别是（）

A、 $b = 4$ ， $c = 2$ B、 $b = - 8$ ， $c = 18$ C、 $b = 4$ ， $c = 6$ D、 $b = - 8$ ， $c = 14$

查看试题解析
8. 如图，量角器的直径与含 $30 °$ 角的直角三角形 $A B C$ 的斜边 $A B$ 重合 $(A$ 点的刻度为 $0)$ ，射线 $C P$ 从 $C A$ 处出发沿顺时针方向以每秒 $2$ 度的速度旋转， $C P$ 与量角器的半圆弧交于点 $E$ ，当第30秒时，点 $E$ 在量角器上对应的读数是（）

A、 $120 °$ B、 $150 °$ C、 $75 °$ D、 $60 °$

查看试题解析
9. 如图，在四边形 $A B C D$ 中 $∠ A D C = ∠ A B C = 90 °$ ， $A D = C D$ ， $D P ⊥ A B$ 于点 $P$ ，若四边形 $A B C D$ 的面积是 $9$ ，则 $D P$ 的长是（）

A、6 B、4.5 C、3 D、2

查看试题解析
10. 如图，正方形 $A B C D$ 的边长为2，对角线 $A C$ 、 $B D$ 相交于点 $O$ ，把 $R t △ O E F$ 放在正方形上，使直角顶点与点 $O$ 重合，让 $R t △ O E F$ 绕着点 $O$ 旋转， $O E$ 、 $O F$ 分别交 $B C$ 、 $C D$ 于点 $M$ 、 $N$ ，给出下列结论；① $B M = C N$ ；② $S_{四边形 O M C N} = 1$ ；③ $M N = O A$ .其中正确的结论是（）

A、①②③ B、①② C、②③ D、①③

查看试题解析

二、填空题

11. 彗星着陆器“菲莱”成功登陆距离地球约5亿公里的彗星.5亿可用科学记数法表示为．

查看试题解析
12. 计算： $| - 2 | - 202 2^{0} =$ ．

查看试题解析
13. 如图，正方形 $A B C D$ 的边长为6， $M$ 为 $A B$ 的中点， $P$ 是 $B C$ 边上的动点，连接 $P M$ ，以点 $P$ 为圆心， $P M$ 长为半径作 $⊙ P$ ，当圆 $P$ 与正方形 $A B C D$ 的边相切时， $B P$ 的长为．

查看试题解析
14. 如图，点A是双曲线y＝﹣ $\frac{9}{x}$ 在第二象限分支上的一个动点，连接AO并延长交另一分支于点B，以AB为底作等腰△ABC，且∠ACB＝120°，点C在第一象限，随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y＝ $\frac{k}{x}$ 上运动，则k的值为.

查看试题解析
15. 已知：正方形的边长为 $5 c m$ ，则对角线的交点到一边的距离为．

查看试题解析
16. 利用二维码可以进行身份识别．某校建立了一个身份识别系统，图1是某个学生的识别图案，黑色小正方形表示1，白色小正方形表示0，将第一行数字从左到右依次记为a，b，c，d，那么可以转换为该生所在班级序号，其序号为a×2³+b×2²+c×2¹+d×2⁰ ．如图1中的第一行数字从左到右依次为0，1，0，1，序号即为0×2³+1×2²+0×2¹+1×2⁰＝5，表示该生为5班学生．若想在图2中表示4班学生的识别图案，请问应该把标号为①、②、③、④的正方形中的（只填序号）涂成黑色．

查看试题解析

三、解答题

17. 在自然数中，一个四位数，记千位数字与个位数字之和为 $x$ ，十位数字与百位数字之和为 $y$ ，如果 $x = y$ ，那么称这个四位数为“对称四位数”．

(1)、在四位数2002和2053中，其中是“对称四位数”；

(2)、最小的“对称四位数”为；

(3)、一个“对称四位数” $M$ ，它的百位数字是千位数字 $a$ 的3倍，个位数字与十位数字之和为8，且千位数字 $a$ 使得不等式组 ${\begin{array}{l} x - 4 \leq 0 \\ x > \frac{a}{3} \end{array}$ 恰有4个整数解，请直接写出所有满足条件的“对称四位数” $M$ 的值．

查看试题解析
18. “足球运球”是中考体育必考项目之一．我市某学校为了解今年九年级学生足球运球的掌握情况，随机抽取部分九年级学生足球运球的测试成绩作为一个样本，按A、B、C、D四个等级进行统计，制成了如图不完整的统计图．

根据所给信息，解答以下问题：

(1)、本次抽样调查抽取了名学生的成绩；在扇形统计图中，D对应的扇形的圆心角是度；

(2)、补全条形统计图；

(3)、所抽取学生的足球运球测试成绩的中位数会落在等级；

(4)、该校九年级有300名学生，请估计足球运球测试成绩达到A级的学生有多少人？

查看试题解析
19. 已知，如图所示直线y=kx+2（k≠0）与反比例函数y= $\frac{m}{x}$ （m≠0）分别交于点P，与y轴、x轴分别交于点A和点B，且cos∠ABO= $\frac{\sqrt{5}}{5}$ ，过P点作x轴的垂线交于点C，连接AC，

(1)、求一次函数的解析式．

(2)、若AC是△PCB的中线，求反比例函数的关系式．

查看试题解析
20. 今年某社区为搞好绿化，计划购买甲、乙两种树苗共计 $n$ 棵．有关甲、乙两种树苗的信息如下框图所示．
$1 .$ 甲种树苗每棵50元
$2 .$ 乙种树苗每棵80元
$3 .$ 甲种树苗的成活率为90%；
$4 .$ 乙种树苗的成活率为95%
要使这批树苗的成活率不低于92%，且使购买这两种树苗的总费用为26000元，求 $n$ 的最大值．

查看试题解析
21. 如图所示，已知 $O A B C$ 是一张放在平面直角坐标系中的矩形纸片，O为坐标原点，点A在x轴上，点C在y轴上，且 $O A = 15 ， O C = 9$ ，在边 $A B$ 上选取一点D，将 $△ A O D$ 沿 $O D$ 翻折，使点A落在 $B C$ 边上，记为点E．

(1)、求 $D E$ 所在直线的解析式；

(2)、设点P在x轴上，以点O、E、P为顶点的三角形是等腰三角形，问这样的点P有几个？并求出所有满足条件的点P的坐标；

(3)、在x轴、y轴上是否分别存在点M、N，使四边形 $M N E D$ 的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由．

查看试题解析
22. 如图，抛物线 $y = - x^{2} + 2 x + c$ 经过点 $P (\frac{5}{2} ， \frac{7}{4})$ ，且交 $y$ 轴于点 $A$ ，点 $C$ 是 $x$ 轴正半轴上的动点， $O E ∥ C P$ 交抛物线于点 $E$ ， $E F ∥ x$ 轴交线段 $C P$ 的延长线于点 $F$ ，作直线， $E P$ 交 $x$ 轴于点 $D$ ，交 $y$ 轴于点 $Q$

(1)、求抛物线的解析式．

(2)、当 $O D$ 为何值时，点 $E$ 恰好与点 $A$ 重合 $\cdot$

(3)、当 $O C = C D$ 时，请直接写出线段 $Q E ︰ E P$ 的值．

查看试题解析
23. 如下4个图中，不同的矩形 $A B C D$ ，若把 $D$ 点沿 $A E$ 对折，使 $D$ 点与 $B C$ 上的 $F$ 点重合；

(1)、图 $①$ 中，若 $D E ： E C = 2 ： 1$ ，求证： $△ A B F ∽ △ A F E ∽ △ F C E$ ；并计算 $B F ： F C$ ．

(2)、图 $②$ 中若 $D E ： E C = 3 ： 1$ ，计算 $B F ： F C =$ ；图 $③$ 中若 $D E ： E C = 4 ： 1$ ，计算 $B F ： F C =$ ．

(3)、图 $④$ 中若 $D E ： E C = n ： 1$ ，猜想 $B F ： F C =$ ▲ ；并证明你的结论．

查看试题解析

平均一天所需时间 $(h)$	5	6	7	9
学生数	4	5	2	1