山东省临沂市2022年中考数学二模试题
试卷更新日期:2023-03-31 类型:中考模拟
一、单选题
-
1. 实数a在数轴上的对应点的位置如图所示,若﹣a<b<a , 则b的值可以是( )
 A、﹣1 B、﹣2 C、2 D、32. 2022年油价多次上涨,新能源车企迎来了更多的关注,如图是理想、蔚来、小鹏、哪吒四款新能源汽车的标志,其中既是轴对称图形,又是中心对称图形的是( )A、
A、﹣1 B、﹣2 C、2 D、32. 2022年油价多次上涨,新能源车企迎来了更多的关注,如图是理想、蔚来、小鹏、哪吒四款新能源汽车的标志,其中既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 计算( )A、a B、–a C、a D、–a4. 函数y= 中自变量x的取值范围在数轴上表示正确的是( )A、
3. 计算( )A、a B、–a C、a D、–a4. 函数y= 中自变量x的取值范围在数轴上表示正确的是( )A、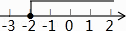 B、
B、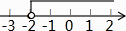 C、
C、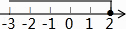 D、
D、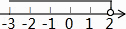 5. 如图,在△ABC中,∠A=46°,∠B=72°.若直线l∥BC,则∠1的度数为( )
5. 如图,在△ABC中,∠A=46°,∠B=72°.若直线l∥BC,则∠1的度数为( )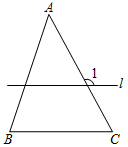 A、117° B、120° C、118° D、128°6. 2021年3月考古人员在山西泉阳发现目前中国规模最大、保存最完好的战国水井,井壁由等长的柏木按原始榫卯结构相互搭接呈闭合的正九边形逐层垒砌,关于正九边形下列说法错误的是( )
A、117° B、120° C、118° D、128°6. 2021年3月考古人员在山西泉阳发现目前中国规模最大、保存最完好的战国水井,井壁由等长的柏木按原始榫卯结构相互搭接呈闭合的正九边形逐层垒砌,关于正九边形下列说法错误的是( )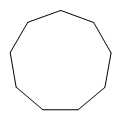 A、它是轴对称图形 B、它是中心对称图形 C、它的外角和是360° D、它的每个内角都是140°7. 电脑上有一个有趣的“扫雷”游戏,图是扫雷游戏的一部分,说明:图中数字2表示在以该数字为中心的周边8个方格中有2个地雷,小旗表示该方格已被探明有地雷,现在还剩下A、B、C三个方格未被探明,其它地方为安全区(包括有数字的方格),则A、B、C三个方格中有地雷的概率最大的方格是( )
A、它是轴对称图形 B、它是中心对称图形 C、它的外角和是360° D、它的每个内角都是140°7. 电脑上有一个有趣的“扫雷”游戏,图是扫雷游戏的一部分,说明:图中数字2表示在以该数字为中心的周边8个方格中有2个地雷,小旗表示该方格已被探明有地雷,现在还剩下A、B、C三个方格未被探明,其它地方为安全区(包括有数字的方格),则A、B、C三个方格中有地雷的概率最大的方格是( )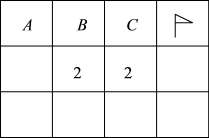 A、A B、B C、C D、无法确定8. 如图,直线AB是⊙O的切线,点C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为( )
A、A B、B C、C D、无法确定8. 如图,直线AB是⊙O的切线,点C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为( )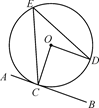 A、30° B、35° C、40° D、45°9. 某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共有了18天完成全部任务.设原计划每天加工x套运动服,根据题意可列方程为A、 B、 C、 D、10. 如图,在平面直角坐标系xOy中,点A的坐标是 , 点B是函数图象上的一个动点,过点B作BC⊥y轴交函数的图象于点C,点D在x轴上(D在A的左侧),且AD=BC,连接AB,CD.有如下四个结论:
A、30° B、35° C、40° D、45°9. 某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共有了18天完成全部任务.设原计划每天加工x套运动服,根据题意可列方程为A、 B、 C、 D、10. 如图,在平面直角坐标系xOy中,点A的坐标是 , 点B是函数图象上的一个动点,过点B作BC⊥y轴交函数的图象于点C,点D在x轴上(D在A的左侧),且AD=BC,连接AB,CD.有如下四个结论:①四边形ABCD可能是菱形;②四边形ABCD可能是正方形;③四边形ABCD的周长是定值;④四边形ABCD的面积是定值.所有正确结论的序号是( )
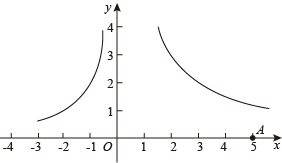 A、①② B、③④ C、①③ D、①④11. 如图,已知抛物线与直线y=x交于和两点,有以下结论:①;②3b+c+6=0;③当时,;④当时, , 其中正确的个数是( )
A、①② B、③④ C、①③ D、①④11. 如图,已知抛物线与直线y=x交于和两点,有以下结论:①;②3b+c+6=0;③当时,;④当时, , 其中正确的个数是( ) A、1 B、2 C、3 D、412. 如图,正方形ABCD的边长为 , 直线EF经过正方形的中心O,并能绕着O转动,分别交AB、CD边于E、F点,过点B作直线EF的垂线BG,垂足为点G,连接AG,则AG长的最小值为( )
A、1 B、2 C、3 D、412. 如图,正方形ABCD的边长为 , 直线EF经过正方形的中心O,并能绕着O转动,分别交AB、CD边于E、F点,过点B作直线EF的垂线BG,垂足为点G,连接AG,则AG长的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 分解因式:ax4﹣81ay4= .14. 如图, 中, , 于 点, 于点 , 于点 , ,则 .
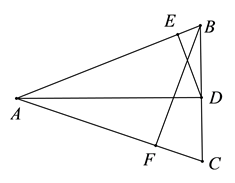 15. 如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A'B′C',其中点B的运动路径为 ,则图中阴影部分的面积为.
15. 如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A'B′C',其中点B的运动路径为 ,则图中阴影部分的面积为.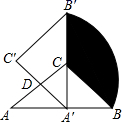 16. P(x1 , y1),P2(x2 , y2)(x1≠x2)是下列函数图象上任意的两点:①y=-3x+1;②y= ;③y=-x2;④y=x2-2x+3(x<0).其中,满足(x1-x2)(y1-y2)<0的函数有 . (填序号)
16. P(x1 , y1),P2(x2 , y2)(x1≠x2)是下列函数图象上任意的两点:①y=-3x+1;②y= ;③y=-x2;④y=x2-2x+3(x<0).其中,满足(x1-x2)(y1-y2)<0的函数有 . (填序号)三、解答题
-
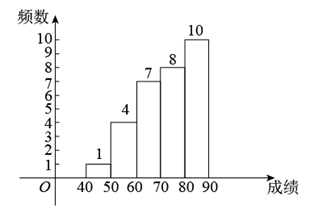
17. 计算与化简题(1)、计算:(2)、先化简,再求代数式的值,其中 .18. 2022年2月20日晚,北京冬奥会在国家体育场上空燃放的绚丽烟花中圆满落幕,伴随着北京冬奥会的举行,全国各地掀起了参与冰上运动、了解冰上运动知识的热潮,为了调查同学们对冬奥知识的了解情况,某校对七八两个年级进行了相关测试,获得了他们的成绩(单位:分),并随机从七八两个年级各抽取30名同学的数据(成绩)
进行了整理、描述和分析.下面给出了相关信息:
a . 七年级测试成绩的数据的频数分布直方图如下(数据分成5组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90):
b . 七年级测试成绩的数据在70≤x<80这一组的是:
70 72 73 75 76 77 78 78
c . 七、八两个年级测试成绩的数据的平均数、中位数、众数如表:
平均数
中位数
众数
七年级
71.1
m
80
八年级
72
73
73
根据以上信息,回答下列问题:
(1)、写出表中m的值;(2)、抽取的测试成绩中,七年级有一个同学A的成绩为75分,八年级恰好也有一位同学B的成绩也是75分,这两名学生在各自年级抽取的测试成绩排名中更靠前的是 , 理由是 .(3)、若七年级共有学生280人,估计七年级所有学生中成绩不低于75分的约有多少人.19. 图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.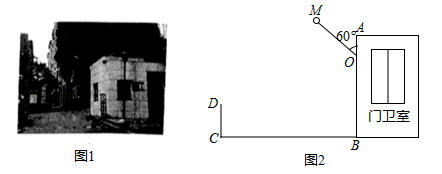 (1)、求点M到地面的距离;(2)、某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据: 1.73,结果精确到0.01米)20. 已知A、B两地之间有一条长240千米的公路.甲车从A地出发匀速开往B地,甲车出发两小时后,乙车从 地出发匀速开往A地,两车同时到达各自的目的地.两车行驶的路程之和y(千米)与甲车行驶的时间x(时)之间的函数关系如图所示.
(1)、求点M到地面的距离;(2)、某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据: 1.73,结果精确到0.01米)20. 已知A、B两地之间有一条长240千米的公路.甲车从A地出发匀速开往B地,甲车出发两小时后,乙车从 地出发匀速开往A地,两车同时到达各自的目的地.两车行驶的路程之和y(千米)与甲车行驶的时间x(时)之间的函数关系如图所示. (1)、甲车的速度为千米/时,a的值为 .(2)、求乙车出发后,y与x之间的函数关系式.(3)、当甲、乙两车相距100千米时,求甲车行驶的时间.21. 如图,AB是⊙O的直径,C是⊙O上一点,过C作⊙O的切线交AB的延长线于点D,连接AC、BC,过O作 , 交BC于G,交DC于F.
(1)、甲车的速度为千米/时,a的值为 .(2)、求乙车出发后,y与x之间的函数关系式.(3)、当甲、乙两车相距100千米时,求甲车行驶的时间.21. 如图,AB是⊙O的直径,C是⊙O上一点,过C作⊙O的切线交AB的延长线于点D,连接AC、BC,过O作 , 交BC于G,交DC于F.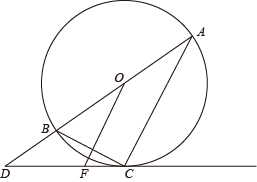 (1)、求证:∠DCB=∠DOF;(2)、若 , BC=4,求OF的长.22. 在平面直角坐标系中,抛物线与x轴的交点为点和点B.(1)、求抛物线的对称轴和点B的坐标;(2)、当a=1,时,求出y的取值范围;(3)、P是抛物线上的一点,若满足△PAB的面积为1的P点有4个,求a的取值范围.23. 勾股定理是数学史上非常重要的一个定理.早在2000多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:如图;分别以Rt△ABC的三边为边长,向外作正方形ABDE、BCFG、ACHI.
(1)、求证:∠DCB=∠DOF;(2)、若 , BC=4,求OF的长.22. 在平面直角坐标系中,抛物线与x轴的交点为点和点B.(1)、求抛物线的对称轴和点B的坐标;(2)、当a=1,时,求出y的取值范围;(3)、P是抛物线上的一点,若满足△PAB的面积为1的P点有4个,求a的取值范围.23. 勾股定理是数学史上非常重要的一个定理.早在2000多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:如图;分别以Rt△ABC的三边为边长,向外作正方形ABDE、BCFG、ACHI.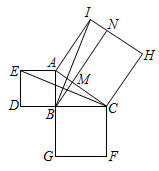 (1)、设正方形ABDE的面积为 , 正方形BCFG的面积为 , 正方形ACHI的面积为 , 证明;(2)、连接BI、CE,求证:EC=BI;(3)、过点B作AC的垂线,交AC于点M,交IH于点N.试说明四边形AMNI与正方形ABDE的面积相等.
(1)、设正方形ABDE的面积为 , 正方形BCFG的面积为 , 正方形ACHI的面积为 , 证明;(2)、连接BI、CE,求证:EC=BI;(3)、过点B作AC的垂线,交AC于点M,交IH于点N.试说明四边形AMNI与正方形ABDE的面积相等.