山东省临沂市沂水县2022年中考一模数学试题

试卷更新日期：2023-03-31 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算：3＋（-7）＝（）

A、4 B、-4 C、10 D、-10

查看试题解析
2. 若二次根式 $\sqrt{a + 2}$ 在实数范围内有意义，则a的取值范围是（）

A、a≥-2 B、a≥2 C、a≤-2 D、a＞-2

查看试题解析
3. 如图，在△ABC中，∠B＝50°，∠C＝70°，直线DE经过点A，∠DAB＝55°，则∠EAC的度数是（）

A、55° B、60° C、65° D、70°

查看试题解析
4. 如图，数轴上有三个点A，B，C，若点A，B表示的数互为相反数，则图中点C对应的数是（）

A、﹣2 B、0 C、1 D、4

查看试题解析
5. 方程组 ${\begin{array}{l} x + y = 2 \\ 3 x + y = 4 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 0 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = - 2 \end{array}$ D、 ${\begin{array}{l} x = 3 \\ y = - 3 \end{array}$

查看试题解析
6. 柜子里有两双不同的鞋，如果从中随机地取出2只，那么取出的鞋是同一双的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{1}{6}$

查看试题解析
7. 下列四张正方形硬纸片，剪去阴影部分后，如果沿虚线折叠，可以围成一个封闭的长方体包装盒的是（）

A、 B、 C、 D、

查看试题解析
8. 已知 $3 4^{2} = 1156$ ， $3 5^{2} = 1225$ ， $3 6^{2} = 1296$ ， $3 7^{2} = 1369$ ．若n为整数且 $n - 1 < \sqrt{1334} < n$ ，则n的值为（）

A、34 B、35 C、36 D、37

查看试题解析
9. 如图，在⊙O中，AB切⊙O于点A，连接OB交⊙O于点C，过点A作AD∥OB交⊙O于点D，连接CD．若∠OCD＝20°，则∠B为（）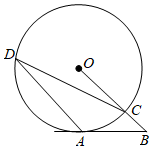

A、30° B、40° C、45° D、50°

查看试题解析
10. 下列等式成立的是（）

A、669²＋2×669×31＋31²＝700² B、669²-669×69-69²＝600² C、669²＋669×31＋31²＝700² D、669²-2×669×69-69²＝600²

查看试题解析
11. 如图，在平行四边形ABCD中，对角线BD＝8，分别以点A，B为圆心，以大于 $\frac{1}{2}$ AB的长为半径画弧，两弧相交于点E和点F，作直线EF，交对角线BD于点G，连接GA，GA恰好垂直于边AD，若GA＝3，则AD的长是（）

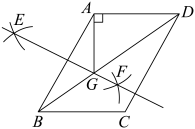A、3 B、4 C、5 D、3 $\sqrt{3}$

查看试题解析
12. 马鸣和杨豪进行4×50米折返跑．在整个过程中，跑步者距起跑线的距离y（单位：m）与跑步时间t（单位：s）的对应关系如图所示．下列叙述：①两人从起跑线同时出发，同时到达终点；②马鸣跑全程的平均速度大于杨豪跑全程的平均速度；③杨豪在跑最后100m的过程中，与马鸣相遇2次；④马鸣前15s跑过的路程大于杨豪前15s跑过的路程．其中错误的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 分解因式： $2 m^{2} - 18 =$ .

查看试题解析
14. 在反比例函数y＝ $\frac{m - 2}{x}$ 的图象的每一支曲线上，函数值y随自变量x的增大而增大，则m的取值范围是．

查看试题解析
15. 如图，在矩形ABCD中，AB＝3，AD＝4，E是边AD的中点．将△ABE沿直线BE翻折，点A落在点F处，连接DF，那么∠EDF的正切值是．

查看试题解析
16. 如图，用一块长7.5cm、宽3cm的长方形纸板，和一块长6cm、宽1.5cm的长方形纸板，与一块小正方形纸板以及另两块长方形纸板，恰好拼成一个大正方形，则小正方形的边长是cm，拼成的大正方形的面积是cm² ．

查看试题解析

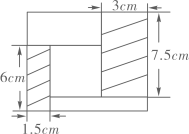
三、解答题

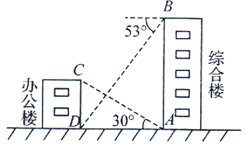
17. 计算： $\sqrt{12} +$ （π﹣2022）⁰﹣2cos30°.

查看试题解析
18. 在一次数学课外实践活动中，小明所在的学习小组从综合楼顶部B处测得办公楼底部D处的俯角是53°，从综合楼底部A处测得办公楼顶部C处的仰角恰好是30°，综合楼高24米.请你帮小明求出办公楼的高度.（结果精确到0.1，参考数据tan37°≈0.75，tan53°≈1.33， $\sqrt{3}$ ≈1.73）

查看试题解析

19. 九（1）班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛，在相同的条件下，分别对两名男生进行了八次一分钟跳绳测试.现将测试结果绘制成如下不完整的统计图表，请根据统计图表中的信息解答下列问题：

	平均数	中位数	众数	方差
甲	175	$a$	$b$	93.75
乙	175	175	180，175，170	$c$

(1)、求

a

、

b

的值；

(2)、若九（1）班选一位成绩稳定的选手参赛，你认为应选谁，请说明理由；

(3)、根据以上的数据分析，请你运用所学统计知识，任选两个角度评价甲乙两名男生一分钟跳绳成绩谁优.

查看试题解析

20. 环保局对某企业排污情况进行检测，结果显示：所排污水中硫化物的浓度达到10mg/L，超过最高允许的1.0mg/L．环保局要求该企业立即整改，在15天以内（含15天）排污达标．整改过程中，所排污水中硫化物的浓度y（mg/L）与时间x（天）的变化规律如表所示．
x（天）
0
1
2
3
4
5
…
y（mg/L）
10
8
6
4
3
2.4
…

(1)、分析说明整改过程中硫化物的浓度y与时间x大致符合怎样的的函数关系？并求其函数表达式；

(2)、该企业所排污水中硫化物的浓度，能否在15天以内不超过最高允许的1.0mg/L？为什么？

查看试题解析
21. 如图，在⊙O中，弦AB，CD互相垂直，垂足为M，F是 $\overset{⌢}{B D}$ 上的一点，且 $\overset{⌢}{B F} = \overset{⌢}{B C}$ ， AF分别与CD，BD相交于点E，N，连接FD，MN．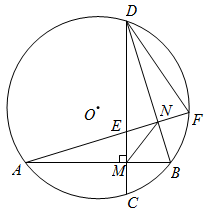

(1)、求证：DE＝DF；

(2)、若⊙O的半径为8，∠BAF＝22.5°，求线段MN的长．

查看试题解析
22. 已知抛物线y＝ax²＋bx＋c（a≠0）经过O（0，0），A（n，0）（n≠0）和B（1，1）三点．

(1)、若该抛物线的顶点恰为点B，求此时n的值，并判断抛物线的开口方向；

(2)、当n＝-2时，确定这个抛物线的解析式，并判断抛物线的开口方向；

(3)、由（1）（2）可知，n的取值变化，会影响该抛物线的开口方向．请你求出n满足什么条件时，抛物线的开口向下？

查看试题解析
23. 如图，在平行四边形ABCD中（AB＜AD），∠BAD＝120°，DE平分∠ADC，交对角线AC于点G，交AB的延长线于点E，将线段EB绕点E顺时针旋转60°得线段EP，连接PA，PB．

(1)、补全图形，判断DE和PB的位置关系，并加以证明；

(2)、求证：AP＝AC；

(3)、若BE＝ $\frac{1}{2}$ AB，直接写出△APE与△CDG面积的比值．

查看试题解析

x（天）	0	1	2	3	4	5	…
y（mg/L）	10	8	6	4	3	2.4	…