山东省临沂市平邑县2022年中考三模数学试题

试卷更新日期：2023-03-31 类型：中考模拟

进入出卷网下载

一、单选题

1. 若 $| x | = 3$ ， $| y | = 4$ ，且 $| x - y | = y - x$ ，则xy的值为（）

A、-1 B、-12 C、12 D、12或-12

查看试题解析
2. 下列标志中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列等式正确的是（）

A、 $| - 3 | + \tan 45 ° = - 2$ B、 ${(x y)}^{5} \div {(\frac{x}{y})}^{5} = x^{10}$ C、 ${(a - b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $x^{3} y - x y^{3} = x y (x + y) (x - y)$

查看试题解析
4. 函数 $y = \frac{1}{\sqrt{x + 1}} + {(x - 2)}^{0}$ 的自变量 $x$ 的取值范围是（）

A、 $x \geq - 1$ B、 $x > 2$ C、 $x > - 1$ 且 $x \neq 2$ D、 $x \neq - 1$ 且 $x \neq 2$

查看试题解析
5. 疫情期间进入学校都要进入测温通道，体温正常才可进入学校，昌平某校有2个测温通道，分别记为A、B通道，学生可随机选取其中的一个通道测温进校园．某日早晨该校所有学生体温正常．小王和小李两同学该日早晨进校园时，选择同一通道测温进校园的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析

6. 世界各国温度的计量单位尚不统一，常用的有摄氏温度（℃）和华氏温度（°F）两种，它们之间的换算关系如下表所示：

摄氏（单位℃）	…	0	1	2	3	4	5	6	…
华氏（单位°F）	…	32	33.8	35.6	37.4	39.2	41	42.8	…

那么当华氏度与摄氏度对应相等时的温度值是（）

A、32 B、－20 C、－40 D、40

查看试题解析

7. 如图，正方形ABCD的对角线AC，BD交于点O，M是边AD上一点，连接OM，过点O作ON⊥OM，交CD于点N．若四边形MOND的面积是1，则AB的长为（）

A、1 B、 $\sqrt{2}$ C、2 D、 $2 \sqrt{2}$

查看试题解析
8. 我国某型号运载火箭的整流罩的三视图如图所示，根据图中数据（单位：米）计算该整流罩的侧面积（单位：平方米）是（）

A、 $7.2 π$ B、 $11.52 π$ C、 $12 π$ D、 $13.44 π$

查看试题解析
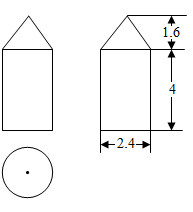9. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，按以下步骤作图：①以 $B$ 为圆心，任意长为半径作弧，分别交 $B A$ 、 $B C$ 于 $M$ 、 $N$ 两点；②分别以 $M$ 、 $N$ 为圆心，以大于 $\frac{1}{2} M N$ 的长为半径作弧，两弧相交于点 $P$ ；③作射线 $B P$ ，交边 $A C$ 于 $D$ 点.若 $A B = 10$ ， $B C = 6$ ，则线段 $C D$ 的长为（）

A、3 B、 $\frac{10}{3}$ C、 $\frac{8}{3}$ D、 $\frac{16}{5}$

查看试题解析
10. 已知点 $P (x_{0} ， y_{0})$ 和直线 $y = k x + b$ ，求点P到直线 $y = k x + b$ 的距离d可用公式 $d = \frac{| k x_{0} - y_{0} + b |}{\sqrt{1 + k^{2}}}$ 计算．根据以上材料解决下面问题：如图， $⊙ C$ 的圆心C的坐标为 $(1 ， 1)$ ，半径为1，直线l的表达式为 $y = - 2 x + 6$ ，P是直线l上的动点，Q是 $⊙ C$ 上的动点，则 $P Q$ 的最小值是（）

A、 $\frac{3 \sqrt{5}}{5}$ B、 $\frac{3 \sqrt{5}}{5} - 1$ C、 $\frac{6 \sqrt{5}}{5} - 1$ D、2

查看试题解析
11. “闻起来臭，吃起来香”的臭豆腐是长沙特色小吃，臭豆腐虽小，但制作流程却比较复杂，其中在进行加工煎炸臭豆腐时，我们把焦脆而不糊的豆腐块数的百分比称为“可食用率”，在特定条件下，“可食用率”p与加工煎炸的时间t（单位：分钟）近似满足函数关系式： $p = a t^{2} + b t + c$ （ $a \neq 0 ，$ a，b，c为常数），如图纪录了三次实验数据，根据上述函数关系和实验数据，可以得到加工煎炸臭豆腐的最佳时间为（）

A、3.50分钟 B、4.05分钟 C、3.75分钟 D、4.25分钟

查看试题解析
12. 如图，矩形OABC起始位置紧贴在坐标轴上，且坐标为C（0，2），A（1，0），将矩形OABC绕其右下角的顶点按顺时针方向旋转90°至图①位置，继续绕右下角的顶点按顺时针方向旋转90°至图②位置，以此类推，这样连续旋转2021次．则顶点A在旋转2021次后的坐标为（）

A、（3030，0） B、（2020，2020） C、（3031，0） D、（3030，2）

查看试题解析

二、填空题

13. 若关于x的方程 $k x^{2} - 6 x + 9 = 0$ 有实数根，则k的取值范围是．

查看试题解析
14. 下表中 $y$ 与 $x$ 的数据满足我们初中学过的某种函数关系，其函数表达式为.

$x$

……

$- 1$

$0$

$1$

$3$

……

$y$

……

$0$

$3$

$4$

$0$

……

查看试题解析
15. 数学课上，李老师提出如下问题：
已知：如图， $A B$ 是⊙O的直径，射线 $A C$ 交⊙O于 $C$ ．

求作：弧 $B C$ 的中点D ．

同学们分享了如下四种方案：

①如图1，连接BC ，作BC的垂直平分线，交⊙O于点D ．

②如图2，过点O作AC的平行线，交⊙O于点D ．

③如图3，作∠BAC的平分线，交⊙O于点D ．

④如图4，在射线AC上截取AE ，使AE=AB ，连接BE ，交⊙O于点D ．

上述四种方案中，正确的方案的序号是．

查看试题解析
16. 如图，在菱形 $A B C D$ 中， $∠ A = 60 °$ ，点M，N是边 $A D$ ， $A B$ 上任意两点，将菱形 $A B C D$ 沿 $M N$ 翻折，点A恰巧落在对角线 $B D$ 上的点E处，下列结论：① $△ M E D ∽ △ E N B$ ；②若 $∠ D M E = 20 °$ ，则 $∠ E N B = 100 °$ ；③若 $D E ： B E = 1 ： 2$ ，则 $A M ： A N = 1 ： 2$ ；④若菱形边长为4，M是 $A D$ 的中点，连接 $M C$ ，则线段 $M C = 2 \sqrt{7}$ ，其中正确的结论有：（填写所有正确结论的序号）

查看试题解析

三、解答题

17. 解不等式组： ${\begin{array}{l} 2 x - 3 < 3 x - 2 \\ 2 (x - 2) \geq 3 x - 6 \end{array}$ ．

查看试题解析

18. “停课不停学，学习不延期”，我市通过教育资源公共服务平台为全市中小学生提供公益在线“空中课堂”，为了解学生每天的学习情况，在全市随机抽取了部分学生进行问卷调查，现将调查情况汇总成如下不完整的表格和统计图．

等级	学习时间 $x / h$	人数/人
A	$x ⩽ 2$	40
B	$2 < x ⩽ 3$	180
C	$3 < x ⩽ 4$	160
D	$x > 4$

(1)、这次参与问卷调查的初中生有人，中位数落在等级里；

(2)、补全条形统计图；

(3)、在扇形统计图中，“A”等级对应的圆心角的度数为度；

(4)、若我市有初中生6.4万人，请根据抽样调查结果，估计全市初中生每天参与“空中课堂”学习时间超过

4 h

的人数．

查看试题解析

19. 图1是疫情期间测温员用“额温枪”对小红测温时的实景图，图2是其侧面示意图，其中枪柄 $B C$ 与手臂 $M C$ 始终在同一直线上，枪身 $B A$ 与额头保持垂直量得胳膊 $M N = 28 c m$ ， $M B = 42 c m$ ，肘关节 $M$ 与枪身端点 $A$ 之间的水平宽度为 $25.3 c m$ （即 $M P$ 的长度），枪身 $B A = 8.5 c m$ .

图1

(1)、求 $∠ A B C$ 的度数；

(2)、测温时规定枪身端点 $A$ 与额头距离范围为 $3 ~ 5 c m$ .在图2中，若测得 $∠ B M N = 68.6 °$ ，小红与测温员之间距离为 $50 c m$ 问此时枪身端点 $A$ 与小红额头的距离是否在规定范围内？并说明理由.（结果保留小数点后一位）
（参考数据： $s i n 66.4 ° \approx 0.92$ ， $c o s 66.4 ° = 0.40$ ， $s i n 23.6 ° \approx 0.40$ ， $\sqrt{2} \approx 1.414$ ）

查看试题解析
20. 古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图，线段AB是⊙O的直径，延长AB至点C，使BC＝OB，点E是线段OB的中点，DE⊥AB交⊙O于点D，点P是⊙O上一动点（不与点A，B重合），连接CD，PE，PC.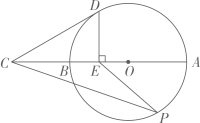

(1)、求证：CD是⊙O的切线；

(2)、小明在研究的过程中发现 $\frac{P E}{P C}$ 是一个确定的值.回答这个确定的值是多少？并对小明发现的结论加以证明.

查看试题解析
21. 在抗击新冠肺炎疫情期间，玉龙社区购买酒精和消毒液两种消毒物资，供居民使用.第一次购买酒精和消毒液若干，酒精每瓶10元，消毒液每瓶5元，共花费了350元；第二次又购买了与第一次相同数量的酒精和消毒液，由于酒精和消毒液每瓶价格分别下降了30%和20%，只花费了260元.

(1)、求每次购买的酒精和消毒液分别是多少瓶？

(2)、若按照第二次购买的价格再一次购买，根据需要，购买的酒精数量是消毒液数量的2倍，现有购买资金200元，则最多能购买消毒液多少瓶？

查看试题解析
22. 函数图象是研究函数的重要工具探究函数性质时，我们经历了列表、描点、连线画出函数图象，然后观察分析图象特征，概括函数性质的过程请结合已有的学习经验，画出函数 $y = - \frac{8 x}{x^{2} + 4}$ 的图象，并探究其性质．

(1)、列表，并在平面直角坐标系中画出该函数的图象；
x
y

(2)、观察函数图象，判断下列关于该函数性质的命题：
①当 $- 2 \leq x \leq 2$ 时，函数图象关于直线 $y = x$ 对称；
②当 $x = 2$ 时，函数有最小值最小值为－2；
③ $- 1 < x < 1$ 时，函数y的值随x的增大而减小
其中正确的是（请写出所有正确命题的序号）

(3)、结合图象，请直接写出不等式 $\frac{8 x}{x^{2} + 4} > x$ 的解集

查看试题解析
23. 在 $△ A B C$ 中， $A B = A C ， ∠ B A C = α$ ，点P为线段 $C A$ 延长线上一动点，连接 $P B$ ，将线段 $P B$ 绕点P逆时针旋转，旋转角为 $α$ ，得到线段 $P D$ ，连接 $D B ， D C$ ．

(1)、如图1，当 $α = 60 °$ 时，请直接写出线段 $P A$ 与线段 $C D$ 的数量关系是， $∠ D C P$ 为度；

(2)、如图2，当 $α = 120 °$ 时，写出线段 $P A$ 和线段 $D C$ 的数量关系，并说明理由；

(3)、如图2，在（2）的条件下，当 $A B = 2 \sqrt{3}$ 时，求 $B P + \frac{1}{3} P C$ 的最小值．

查看试题解析

$x$	……	$- 1$	$0$	$1$	$3$	……
$y$	……	$0$	$3$	$4$	$0$	……