山东省临沂市费县2022年中考二模数学试题
试卷更新日期:2023-03-31 类型:中考模拟
一、单选题
-
1. 2022的倒数是( )A、 B、 C、2022 D、-20222. 下列多边形中,内角和最大的是( )A、
 B、
B、 C、
C、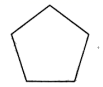 D、
D、 3. 下列各式中,计算正确的是( )A、 B、 C、x3÷x2=x D、(x3)2=x94. 下列等式成立的是( )A、 B、 C、 D、5. 下列调查中,最适合采用全面调查的是( )A、对长江水质状况的调查 B、对全国中学生近视率情况的调查 C、对参加北京冬奥会的运动员进行新冠病毒核酸检测 D、了解一批节能灯的使用寿命6. 如图,在中, , 的平分线分别交于点E,F,若 , , 则EF的长是( )
3. 下列各式中,计算正确的是( )A、 B、 C、x3÷x2=x D、(x3)2=x94. 下列等式成立的是( )A、 B、 C、 D、5. 下列调查中,最适合采用全面调查的是( )A、对长江水质状况的调查 B、对全国中学生近视率情况的调查 C、对参加北京冬奥会的运动员进行新冠病毒核酸检测 D、了解一批节能灯的使用寿命6. 如图,在中, , 的平分线分别交于点E,F,若 , , 则EF的长是( ) A、2 B、2.5 C、3 D、3.57. 为了方便市民就近采集核酸,我市最近增设了一批核酸采样点,争取让市民步行15分钟之内就能找到核酸采样点,甲、乙两人各自随机选择到A,B两个新冠病毒核酸检测点进行核酸检测.这两人都在A检测点进行检测的概率是( ).A、 B、 C、 D、8. 不等式组 的解集在数轴上表示正确的是( )A、
A、2 B、2.5 C、3 D、3.57. 为了方便市民就近采集核酸,我市最近增设了一批核酸采样点,争取让市民步行15分钟之内就能找到核酸采样点,甲、乙两人各自随机选择到A,B两个新冠病毒核酸检测点进行核酸检测.这两人都在A检测点进行检测的概率是( ).A、 B、 C、 D、8. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、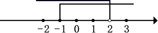 D、
D、 9. 参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是( )A、 x(x+1)=110 B、 x(x﹣1)=110 C、x(x+1)=110 D、x(x﹣1)=11010. 已知线段AB,按如下步骤作图:①作射线AC,使AC⊥AB;②作∠BAC的平分线AD;③以点A为圆心,AB长为半径作弧,交AD于点E;④过点E作EP⊥AB于点P,则AP:AB=( )
9. 参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是( )A、 x(x+1)=110 B、 x(x﹣1)=110 C、x(x+1)=110 D、x(x﹣1)=11010. 已知线段AB,按如下步骤作图:①作射线AC,使AC⊥AB;②作∠BAC的平分线AD;③以点A为圆心,AB长为半径作弧,交AD于点E;④过点E作EP⊥AB于点P,则AP:AB=( )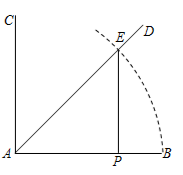 A、 B、 C、 D、11. 如图,在中, , 以点A为圆心,3为半径的圆与边相切于点D,与 , 分别交于点E和点G,点F是优弧上一点, , 则的度数是( )
A、 B、 C、 D、11. 如图,在中, , 以点A为圆心,3为半径的圆与边相切于点D,与 , 分别交于点E和点G,点F是优弧上一点, , 则的度数是( )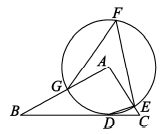 A、50° B、48° C、45° D、36°12. 在平面直角坐标系xOy中,过O点的直线AB分别交函数 , 的图象于点A,B,作轴于点C,作交的图象于点D,连接OD.若的面积为2,则k的值等于( ).A、-6 B、-8 C、-10 D、-12
A、50° B、48° C、45° D、36°12. 在平面直角坐标系xOy中,过O点的直线AB分别交函数 , 的图象于点A,B,作轴于点C,作交的图象于点D,连接OD.若的面积为2,则k的值等于( ).A、-6 B、-8 C、-10 D、-12二、填空题
-
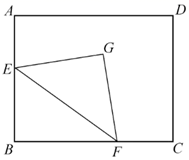
13. 若二次根式 在实数范围内有意义,则 的取值范围是.14. 分解因式 .15. 用一个圆心角为 , 半径为的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .16. 如图,在矩形 中, ,点E,F分别是边 上的动点,点E不与A,B重合,且 ,G是五边形 内满足 且 的点.现给出以下结论:
① 与 一定互补;
②点G到边 的距离一定相等;
③点G到边 的距离可能相等;
④点G到边 的距离的最大值为 .
其中正确的是.(写出所有正确结论的序号)
三、解答题
-
17. 先化简,再求值: , 其中 .18. 今年是中国共产主义青年团成立100周年,某校为了了解八年级510名同学对共青团知识的掌握情况,对他们进行了共青团知识测试.现随机抽取甲、乙两班各15名同学的测试成绩(满分100分)进行整理分析过程如下:
【收集数据】
甲班15名学生测试成绩分别为:78,83,89,97,98,85,100,94,87,90,93,92,99,95,100.
乙班15名学生测试成绩中的成绩如下:91,92,94,90,93.
【整理数据】
班级
甲
1
1
3
4
6
乙
1
2
3
5
4
【分析数据】
班级
平均数
众数
中位数
方差
甲
92
a
93
47.3
乙
90
87
b
50.2
【应用数据】
(1)、根据以上信息,可以求出:a=分,b=分;(2)、若规定测试成绩90分及以上为优秀,请估计参加本次测试的510名学生中成绩为优秀的有多少人;(3)、根据以上数据,你认为哪个班本次测试的整体成绩较好?请说明理由(理由不少于两条).19. 人字折叠梯完全打开后如图1所示,B,C是折叠梯的两个着地点,D是折叠梯最高级踏板的固定点.图2是它的示意图,已知 , , , 求点D离地面的高DE.(结果取整数,参考数据: , , )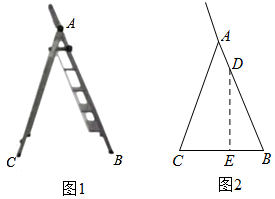 20. 如图,AB为的直径,C为上一点,过点C作的切线CE,过点B作于点D,交于点F,连接AF.
20. 如图,AB为的直径,C为上一点,过点C作的切线CE,过点B作于点D,交于点F,连接AF.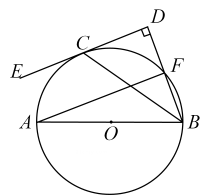 (1)、求证:;(2)、若 , 的半径等于4.5,求DF的长。21. 某超市每天从农场购进甲、乙两种有机蔬菜进行销售,两种蔬菜的进价和售价如下:
(1)、求证:;(2)、若 , 的半径等于4.5,求DF的长。21. 某超市每天从农场购进甲、乙两种有机蔬菜进行销售,两种蔬菜的进价和售价如下:品种
进价(元/斤)
售价(元/斤)
甲
3.5
5
乙
6
7
超市每天购进两种蔬菜共300斤,并在当天都销售完,其中销售甲种蔬菜不少于80斤且不超过120斤,设每天销售甲种蔬菜x斤,当天销售这两种蔬菜总获利W元(销售过程中损耗不计).
(1)、求出W与x的函数关系式,并确定当天销售这两种蔬菜的最大利润;(2)、五一节超市让利销售,将甲种蔬菜售价降低a元/斤,为了保证当天销售这两种蔬菜总获利的最小值不低于320元,求a的最大值.22. 如图1所示的某种发石车是古代一种远程攻击的武器,发射出去的石块的运动轨迹是抛物线的一部分,且距离发射点20米时达到最大高度10米.将发石车置于山坡底部O处,山坡上有一点A,点A与点O的水平距离为30米,与地面的竖直距离为3米,AB是高度为3米的防御墙.若以点O为原点,建立如图2所示的平面直角坐标系. (1)、求石块运动轨迹所在抛物线的解析式;(2)、试通过计算说明石块能否飞越防御墙AB;(3)、在竖直方向上,试求石块飞行时与坡面OA的最大距离.23. 如图,正方形ABCD的边长为6,点E为射线AB上的动点,连接DE,作点A关于DE的对称点F,连接DF,EF,BF,CF.
(1)、求石块运动轨迹所在抛物线的解析式;(2)、试通过计算说明石块能否飞越防御墙AB;(3)、在竖直方向上,试求石块飞行时与坡面OA的最大距离.23. 如图,正方形ABCD的边长为6,点E为射线AB上的动点,连接DE,作点A关于DE的对称点F,连接DF,EF,BF,CF.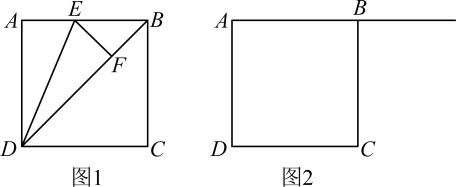 (1)、如图1,当点F落在BD上时,求BE的长;(2)、点E在射线AB上运动的过程中,是否存在为等腰三角形的位置,若存在,求AE的长,若不存在,说明理由.
(1)、如图1,当点F落在BD上时,求BE的长;(2)、点E在射线AB上运动的过程中,是否存在为等腰三角形的位置,若存在,求AE的长,若不存在,说明理由.