山东省聊城市阳谷县2022年中考二模数学试题
试卷更新日期:2023-03-31 类型:中考模拟
一、单选题
-
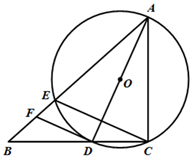
1. 2022的相反数是( )A、2022 B、-2022 C、 D、2. 用7个大小相同的小正方体组成如图所示的几何体,其主视图、俯视图、左视图的面积分别为 , , , 则 , , 的大小关系为( )
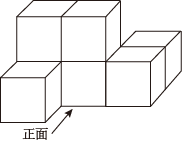 A、 B、 C、 D、3. 一滴水有个水分子,一个水分子的质量大约为克,则一滴水的质量大约为( )A、 B、 C、 D、4. 用尺规作图作三角形的内切圆,用到了哪个基本作图( )A、作一条线段等于已知线段 B、作一个角等于已知角 C、作一个角的平分线 D、作一条线段的垂直平分线5. 下列判断正确的是( )A、一组数据6,5,8,7,9的中位数是8 B、“三角形的内角和为180°”是必然事件 C、甲、乙两组学生身高的方差分别为s甲2=1.6,s乙2=0.8,则甲组学生的身高较整齐 D、神舟十三号卫星发射前的零件检查,应选择抽样调查6. 下列运算正确的是( )A、(m+2)2=m2+4 B、m5-m3=m2 C、(-m2n)3=-m6n3 D、-2m(2m3-m)=-4m4-2m27. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根8. 如图,为直径,点A,D在上, , 若 , 则的长为( )
A、 B、 C、 D、3. 一滴水有个水分子,一个水分子的质量大约为克,则一滴水的质量大约为( )A、 B、 C、 D、4. 用尺规作图作三角形的内切圆,用到了哪个基本作图( )A、作一条线段等于已知线段 B、作一个角等于已知角 C、作一个角的平分线 D、作一条线段的垂直平分线5. 下列判断正确的是( )A、一组数据6,5,8,7,9的中位数是8 B、“三角形的内角和为180°”是必然事件 C、甲、乙两组学生身高的方差分别为s甲2=1.6,s乙2=0.8,则甲组学生的身高较整齐 D、神舟十三号卫星发射前的零件检查,应选择抽样调查6. 下列运算正确的是( )A、(m+2)2=m2+4 B、m5-m3=m2 C、(-m2n)3=-m6n3 D、-2m(2m3-m)=-4m4-2m27. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根8. 如图,为直径,点A,D在上, , 若 , 则的长为( )
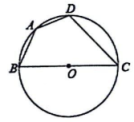 A、2 B、1 C、 D、9. 不等式组的整数解的个数是( )A、2个 B、3个 C、4个 D、5个10. 如图,在直角坐标系中,以坐标原点 , , 为顶点的 , 其两个锐角对应的外角角平分线相交于点P,则P点的横坐标为( )
A、2 B、1 C、 D、9. 不等式组的整数解的个数是( )A、2个 B、3个 C、4个 D、5个10. 如图,在直角坐标系中,以坐标原点 , , 为顶点的 , 其两个锐角对应的外角角平分线相交于点P,则P点的横坐标为( )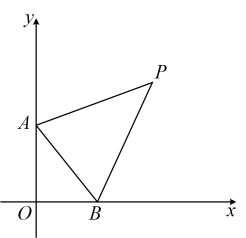 A、5 B、6 C、7 D、811. 将按如图方式放置在平面直角坐标系中,其中 , , 顶点A的坐标为 , 将绕原点逆时针旋转,每次旋转60°,则第2022次旋转结束时,点A对应点的坐标为( )
A、5 B、6 C、7 D、811. 将按如图方式放置在平面直角坐标系中,其中 , , 顶点A的坐标为 , 将绕原点逆时针旋转,每次旋转60°,则第2022次旋转结束时,点A对应点的坐标为( )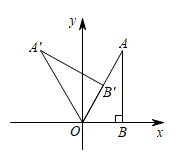 A、 B、 C、 D、12. 如图,四边形是菱形,边长为4, , 垂直于的直线从点A出发,沿AD方向以每秒1个单位长度的速度向右平移,设直线EF与菱形的两边分别交于点E,F(点E在点F的上方),若的面积为y,直线的运动时间为x秒(),则能大致反映y与x的函数关系的图象是( )
A、 B、 C、 D、12. 如图,四边形是菱形,边长为4, , 垂直于的直线从点A出发,沿AD方向以每秒1个单位长度的速度向右平移,设直线EF与菱形的两边分别交于点E,F(点E在点F的上方),若的面积为y,直线的运动时间为x秒(),则能大致反映y与x的函数关系的图象是( ) A、
A、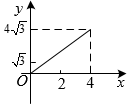 B、
B、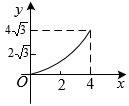 C、
C、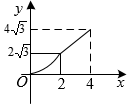 D、
D、
二、填空题
-
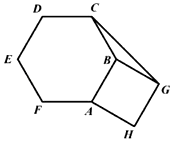
13. 计算结果是 .14. 若数列7、9、11、a、13的平均数为10.5,则a的值为 .15. 一个圆锥的侧面展开图的扇形的圆心角为150度,母线长为12cm,则圆锥的高为cm.16. 如图,六边形ABCDEF为正六边形,四边形ABGH为正方形,则∠BCG的度数为.
 17. 平面直角坐标系中,将抛物线平移得到抛物线C,如图所示,且抛物线C经过点和 , 点P是抛物线C上第一象限内一动点,过点P作x轴的垂线,垂足为Q,则的最大值为 .
17. 平面直角坐标系中,将抛物线平移得到抛物线C,如图所示,且抛物线C经过点和 , 点P是抛物线C上第一象限内一动点,过点P作x轴的垂线,垂足为Q,则的最大值为 .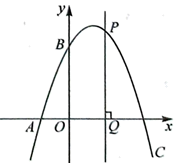
三、解答题
-
18. 计算:20220-|1-|+2sin45°+(-2)-1 .19. 河南省对居民生活用电采用阶梯电价,鼓励居民节约用电,其中年用电量为2160千瓦时及以下执行基础电价0.56元/千瓦时;2160~3120千瓦时的部分按0.61元/千瓦时收费;超过3120千瓦时的部分按0.86元/千瓦时收费.为了解某小区居民生活用电情况.调查小组从该小区随机调查了200户居民的月平均用电量x(千瓦时),并将全部调查数据分组统计如下:
组别
频数(户数)
28
42
a
30
20
10
把这200个数据从小到大排列后,其中第96到第105(包含第96和第105这两个数据)个数据依次为:
148 148 150 152 152 154 160 161 161 162
根据以上信息,回答下列问题:
(1)、本次调查中,该小区居民月平均用电量的中位数为 , 上表a= .(2)、估计该小区能享受基础电价的居民占全小区的百分比.(3)、国家在制订收费标准时,为了减轻居民用电负担,制订的收费标准能让85%的用户享受基础电价.请你根据以上信息对该小区居民的用电情况进行评价,并写出一条建议.20. 为了净化环境,某公司准备购进甲、乙两种型号的洒水车,已知用240万元购进的甲种型号的洒水车比用300万元购进的乙型洒水车少4辆,每台甲型洒水车的价格是乙型洒水车的倍.(1)、求每辆乙型洒水车多少万元?(2)、该公司决定购进两种型号的洒水车共10台,总费用不超过340万元,那么最多购进甲型号的洒水车多少台?21. 如图,在四边形ABCD的中,AB∥CD,对角线AC,BD相交于点O,且AO=CO,△OAB是等边三角形.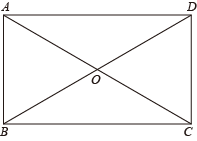 (1)、求证:四边形ABCD是矩形;(2)、若S四边形ABCD=4 , 求BD的长.22. 从2019年底以来,新冠疫情一直困扰着我们的日常生活,今年为进一步加强疫情防控工作,某公司决定安装红外线体温检测仪,这种设备的原理是采用非接触式测温法,只要用红外体温测试仪的镜头对准被测对象进行扫描,其体温就可立刻在显示屏上显示出来,从而有效地避免了其他常规测温法所可能造成的交叉感染,测温区域示意图如图所示,已知最大探测角∠PAO=75°,最小探测角∠PBO=30°.(参考数据:=1.414,=1.732,=2.236)
(1)、求证:四边形ABCD是矩形;(2)、若S四边形ABCD=4 , 求BD的长.22. 从2019年底以来,新冠疫情一直困扰着我们的日常生活,今年为进一步加强疫情防控工作,某公司决定安装红外线体温检测仪,这种设备的原理是采用非接触式测温法,只要用红外体温测试仪的镜头对准被测对象进行扫描,其体温就可立刻在显示屏上显示出来,从而有效地避免了其他常规测温法所可能造成的交叉感染,测温区域示意图如图所示,已知最大探测角∠PAO=75°,最小探测角∠PBO=30°.(参考数据:=1.414,=1.732,=2.236)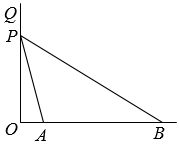 (1)、若该设备安装在离水平地面距离为2.2m的P处,即OP=2.2m,请求出图中OB的长度;(结果精确到0.1m)(2)、若该公司要求测温区域AB的长度为4 m,请求出该设备的安装高度OP的高度.(结果精确到0.1 m)23. 如图,在直角坐标系中,已知点B(4,0),等边三角形OAB的顶点A在反比例函数y(k>0)的图象上.
(1)、若该设备安装在离水平地面距离为2.2m的P处,即OP=2.2m,请求出图中OB的长度;(结果精确到0.1m)(2)、若该公司要求测温区域AB的长度为4 m,请求出该设备的安装高度OP的高度.(结果精确到0.1 m)23. 如图,在直角坐标系中,已知点B(4,0),等边三角形OAB的顶点A在反比例函数y(k>0)的图象上.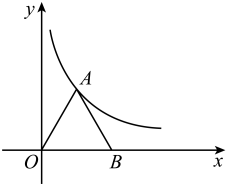 (1)、求反比例函数的表达式;(2)、把△OAB向上平移得到△O'A'B',当点B'恰好经过反比例函数图象时,求△OAB和△O'A'B'重叠部分的面积.
(1)、求反比例函数的表达式;(2)、把△OAB向上平移得到△O'A'B',当点B'恰好经过反比例函数图象时,求△OAB和△O'A'B'重叠部分的面积.