山东省聊城市莘县2022年中考三模数学试题
试卷更新日期:2023-03-31 类型:中考模拟
一、单选题
-
1. 下列各数:-4,-2.8,0, , 其中比小的数是( )A、-4 B、 C、0 D、-2.82. 直六棱柱如图所示,它的俯视图是( )
 A、
A、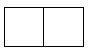 B、
B、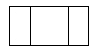 C、
C、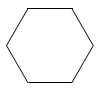 D、
D、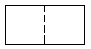 3. 如图, , ,若 ,那么 的度数是( )
3. 如图, , ,若 ,那么 的度数是( )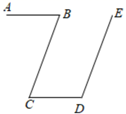 A、 B、 C、 D、4. 下列计算中,正确的是( )A、 B、 C、 D、5. 为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,调查了一个班50名学生每天的睡眠时间,绘成睡眠时间频数分布直方图如图所示,则所调查学生睡眠时间的众数,中位数分别为( )
A、 B、 C、 D、4. 下列计算中,正确的是( )A、 B、 C、 D、5. 为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,调查了一个班50名学生每天的睡眠时间,绘成睡眠时间频数分布直方图如图所示,则所调查学生睡眠时间的众数,中位数分别为( )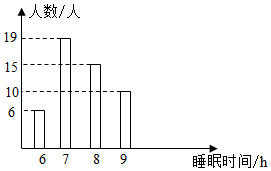 A、7h , 7h B、8h , 7.5h C、7h , 7.5h D、8h , 8h6. 若不等式组的解集是 , 则m的取值范围是( )A、 B、 C、 D、7. 计算的结果为( )A、 B、 C、3 D、48. 如图, 是 的直径, 是 上两点,若 ,则 的度数是( )
A、7h , 7h B、8h , 7.5h C、7h , 7.5h D、8h , 8h6. 若不等式组的解集是 , 则m的取值范围是( )A、 B、 C、 D、7. 计算的结果为( )A、 B、 C、3 D、48. 如图, 是 的直径, 是 上两点,若 ,则 的度数是( ) A、 B、 C、 D、9. 函数 的图象如图所示,则关于x的一元二次方程 的根的情况是( )
A、 B、 C、 D、9. 函数 的图象如图所示,则关于x的一元二次方程 的根的情况是( )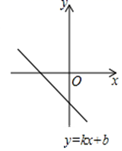 A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定10. “数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,甲烷的化学式CH4 , 乙烷的化学式是C2H6 , 丙烷的化学式是C3H8 , …,设碳原子的数目为n(n为正整数),则它们的化学式都可以用下列哪个式子来表示( )
A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定10. “数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,甲烷的化学式CH4 , 乙烷的化学式是C2H6 , 丙烷的化学式是C3H8 , …,设碳原子的数目为n(n为正整数),则它们的化学式都可以用下列哪个式子来表示( )
A、CnH2n+2 B、CnH2n C、CnH2n﹣2 D、CnHn+311. 在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )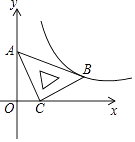 A、( ,0) B、(2,0) C、( ,0) D、(3,0)12. 如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,过点P作PD⊥AB于点D,设运动时间为x(s),△ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是( )
A、( ,0) B、(2,0) C、( ,0) D、(3,0)12. 如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,过点P作PD⊥AB于点D,设运动时间为x(s),△ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 定义a※b=a(b+1),例如2※3=2×(3+1)=2×4=8.则(x﹣1)※x的结果为 .14. 如图所示, 是放置在正方形网格中的一个角,则 的值是.
 15. 如图,从一块半径为 的圆形铁皮上剪出一个圆周角为120°的扇形 ,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为 .
15. 如图,从一块半径为 的圆形铁皮上剪出一个圆周角为120°的扇形 ,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为 .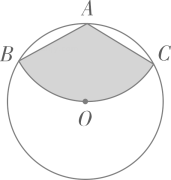 16. 如图,AB是⊙O的直径,点D是AB延长线上的一点,点C在⊙O上,且AC=CD,∠ACD=120°.若⊙O的半径为3,则图中阴影部分的面积为 .
16. 如图,AB是⊙O的直径,点D是AB延长线上的一点,点C在⊙O上,且AC=CD,∠ACD=120°.若⊙O的半径为3,则图中阴影部分的面积为 .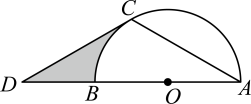 17. 如图,在平面直角坐标系中,直线 : 交x轴于点A,交y轴于点 ,点 , ,…在直线 上,点 , , ,…在x轴的正半轴上,若 , , ,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形 顶点 的横坐标为 .
17. 如图,在平面直角坐标系中,直线 : 交x轴于点A,交y轴于点 ,点 , ,…在直线 上,点 , , ,…在x轴的正半轴上,若 , , ,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形 顶点 的横坐标为 .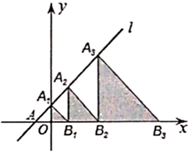
三、解答题
-
18. 先化简,再求值: , 其中 .19. “校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
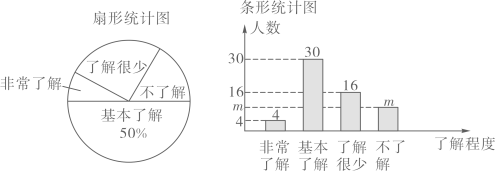 (1)、接受问卷调查的学生共有人,条形统计图中的值为;(2)、若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为人;(3)、若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.20. 在“抗击疫情”期间,某学校工会号召广大教师积极开展了“献爱心捐款”活动,学校拟用这笔捐款购买A、B两种防疫物品.如果购买A种物品60件,B种物品45件,共需1140元;如果购买A种物品45件,B种物品30件,共需840元.(1)、求A、B两种防疫物品每件各多少元;(2)、现要购买A、B两种防疫物品共600件,总费用不超过7000元,那么A种防疫物品最多购买多少件?21. 如图,在 中,点O是AC边的一个动点,过点O作 ,交 的平分线于点E,交 的外角平分线于点F,
(1)、接受问卷调查的学生共有人,条形统计图中的值为;(2)、若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为人;(3)、若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.20. 在“抗击疫情”期间,某学校工会号召广大教师积极开展了“献爱心捐款”活动,学校拟用这笔捐款购买A、B两种防疫物品.如果购买A种物品60件,B种物品45件,共需1140元;如果购买A种物品45件,B种物品30件,共需840元.(1)、求A、B两种防疫物品每件各多少元;(2)、现要购买A、B两种防疫物品共600件,总费用不超过7000元,那么A种防疫物品最多购买多少件?21. 如图,在 中,点O是AC边的一个动点,过点O作 ,交 的平分线于点E,交 的外角平分线于点F, (1)、求证: ;(2)、当点O位于AC边的什么位置时四边形AECF是矩形?并说明理由.22. 如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔AB的高度,他从古塔底部点B处前行30m到达斜坡CE的底部点C处,然后沿斜坡CE前行20m到达最佳测量点D处,在点D处测得塔顶A的仰角为30°,已知斜坡的斜面坡度且点A,B,C,D,E在同一平面内.小明同学测得古塔AB的高度是多少?
(1)、求证: ;(2)、当点O位于AC边的什么位置时四边形AECF是矩形?并说明理由.22. 如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔AB的高度,他从古塔底部点B处前行30m到达斜坡CE的底部点C处,然后沿斜坡CE前行20m到达最佳测量点D处,在点D处测得塔顶A的仰角为30°,已知斜坡的斜面坡度且点A,B,C,D,E在同一平面内.小明同学测得古塔AB的高度是多少? 23. 如图, 中, , ,点 ,点 ,反比例函数 的图象经过点A .
23. 如图, 中, , ,点 ,点 ,反比例函数 的图象经过点A .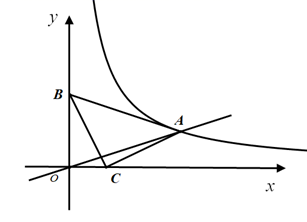 (1)、求反比例函数的解析式;(2)、将直线 向上平移m个单位后经过反比例函数,图象上的点 ,求m,n的值.24. 如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D,过点A作⊙O的切线与OD的延长线交于点P,PC、AB的延长线交于点F.
(1)、求反比例函数的解析式;(2)、将直线 向上平移m个单位后经过反比例函数,图象上的点 ,求m,n的值.24. 如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D,过点A作⊙O的切线与OD的延长线交于点P,PC、AB的延长线交于点F.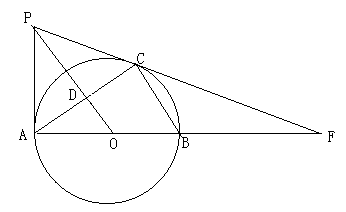 (1)、求证:PC是⊙O的切线;(2)、若∠ABC=60°,AB=10,求线段CF的长,
(1)、求证:PC是⊙O的切线;(2)、若∠ABC=60°,AB=10,求线段CF的长,
25. 如图,直线 分别交x轴、y轴于点A , B , 过点A的抛物线 与x轴的另一交点为C , 与y轴交于点 ,抛物线的对称轴l交 于E , 连接 交 于点F .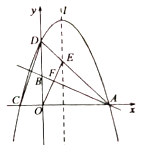 (1)、求抛物线解析式;(2)、求证: ;(3)、P为抛物线上的一动点,直线 交 于点M , 是否存在这样的点P , 使以A , O , M为顶点的三角形与 相似?若存在,求点P的横坐标;若不存在,请说明理由.
(1)、求抛物线解析式;(2)、求证: ;(3)、P为抛物线上的一动点,直线 交 于点M , 是否存在这样的点P , 使以A , O , M为顶点的三角形与 相似?若存在,求点P的横坐标;若不存在,请说明理由.