山东省济宁市金乡县2022年中考三模数学试题

试卷更新日期：2023-03-31 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数是无理数的是（）

A、0 B、 $\sqrt[3]{27}$ C、1.010010001… D、﹣ $\frac{1}{3}$

查看试题解析
2. 要调查下列问题，适合采用全面调查(普查)的是（）

A、中央电视台《开学第一课》的收视率 B、某城市居民6月份人均网上购物的次数 C、即将发射的气象卫星的零部件质量 D、某品牌新能源汽车的最大续航里程

查看试题解析
3. 下列计算正确的是（）

A、 ${(a^{5})}^{2} = a^{10}$ B、 $x^{16} \div x^{4} = x^{4}$ C、 $2 a^{2} + 3 a^{2} = 6 a^{4}$ D、 $b^{3} \cdot b^{3} = 2 b^{3}$

查看试题解析
4. 如图， $△ A B C$ 的顶点都是正方形网格中的格点，则 $c o s ∠ A B C$ 的值为（）

A、 $\frac{3 \sqrt{5}}{10}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{1}{2}$

查看试题解析
5. 不等式组 ${\begin{array}{l} 1 - x \leq 4 \\ \frac{x + 1}{2} < 1 \end{array}$ 解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，圆O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作圆O的切线，交AB的延长线于点D，则∠D的度数是（）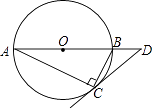

A、25° B、40° C、50° D、65°

查看试题解析
7. 若方程 $x^{2} - 2 x - 4 = 0$ 的两个实数根为α,β，则α $^{2}$ +β $^{2}$ 的值为（　　）

A、12 B、10 C、4 D、-4

查看试题解析
8. 定义新运算：a⊕b= ${\begin{array}{l} \frac{a}{b} (b > 0) \\ - \frac{a}{b} (b < 0) \end{array}$ 例如：4⊕5= $\frac{4}{5}$ ， 4⊕（-5）= $\frac{4}{5}$ ．则函数y=2⊕x（x≠0）的图象大致是（）

A、 B、 C、 D、

查看试题解析
9. 已知：如图，在平面直角坐标系中，有菱形OABC，点A的坐标为（10，0），对角线OB、AC相交于点D，双曲线y= $\frac{k}{x}$ （x＞0）经过点D，交BC的延长线于点E，且OB•AC=160，有下列四个结论：
①双曲线的解析式为y= $\frac{40}{x}$ （x＞0）；②点E的坐标是（4，8）；③sin∠COA= $\frac{4}{5}$ ；④AC+OB=12 $\sqrt{5}$ ．
其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 边长为a的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），…，按此方式依次操作，则第6个正六边形的边长为（）

A、 $\frac{1}{3} \times （ \frac{1}{2} ）^{5} a$ B、 $\frac{1}{2} \times （ \frac{1}{3} ）^{5} a$ C、 $\frac{1}{3} \times （ \frac{1}{2} ）^{6} a$ D、 $\frac{1}{2} \times （ \frac{1}{3} ）^{6} a$

查看试题解析

二、填空题

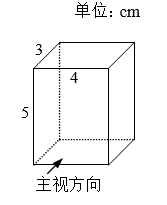
11. 若3x^m⁺⁵y²与x³yⁿ的和是单项式，则n^m=

查看试题解析
12. 如图为一个长方体，则该几何体主视图的面积为cm².

查看试题解析
13. 如图，在△ABC中，∠BAC=90°，AD是BC边上的高，E、F分别是AB、AC边的中点，若AB=8，AC=6，则△DEF的周长为．

查看试题解析
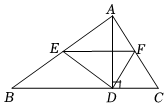14. 如果点P（x，y）的坐标满足x+y=xy，那么称点P为“和谐点”，若某个“和谐点“P到x轴的距离为2，则P点的坐标为.

查看试题解析
15. 如图，A、B、C、D依次为一直线上4个点，BC=2，△BCE为等边三角形，⊙O过A、D、E 三点，且∠AOD=120°．设AB=x，CD=y，则y与x的函数关系式为．（写出自变量的取值范围）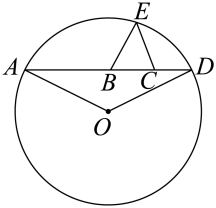

查看试题解析

三、解答题

16. 先化简，再求值： $(\frac{2}{x - 3} + \frac{x}{3 - x}) \div \frac{x - 2}{x^{2} - 6 x + 9}$ ，其中x＝－1．

查看试题解析
17. 用圆规、直尺作图，不写作法，但要保留作图痕迹．
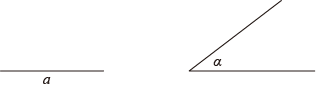
已知：线段a和 $∠ α$ ．

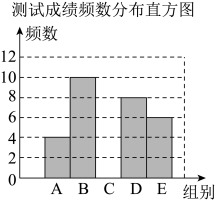
(1)、求作：菱形ABCD，使菱形ABCD的边长为a，其中一个内角 $∠ A$ 等于 $∠ α$ ．

(2)、若菱形ABCD的边长 $a = 2$ cm， $∠ A = 60 °$ ，则此菱形ABCD的面积为cm²

查看试题解析
18. 某中学为检验思想政治课的学习效果，对八年级学生进行“社会主义核心价值观”知识测试（满分100分），随机抽取部分学生的测试成绩进行统计，并将统计结果绘制成如下尚不完整的统计图表：
测试成绩频数分布表
组别
成绩分组
频数
频率
A
50≤x＜60
4
0.1
B
60≤x＜70
10
0.25
C
70≤x＜80
m
n
D
80≤x＜90
8
0.2
E
90≤x≤100
6
0.15
根据以上信息解答下列问题：

(1)、填空：m＝， n＝．

(2)、补全频数分布直方图．

(3)、若要画出该组数据的扇形统计图，请计算C组所在扇形的圆心角度数为．

(4)、学校计划对测试成绩达到80分及以上的同学进行表彰，若该校共有400人参加此次知识测试，请估计受到表彰的学生人数．

查看试题解析
19. 已知∠MPN的两边分别与⊙O相切于点A，B，⊙O的半径为r．

(1)、如图1，点C在点A，B之间的优弧上，∠MPN=80°，求∠ACB的度数：

(2)、如图2，点C在圆上运动，当PC最大时，要使四边形APBC为菱形，∠APB的度数应为多少？请说明理由；

(3)、若PC交⊙O于点D，求第（2）问中对应的阴影部分的周长（用含r的式子表示），

查看试题解析
20. 甲乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，轿车比货车晚出发1.5小时，如图，线段OA表示货车离甲地的距离y（千米）与时间x（小时）之间的函数关系；折线BCD表示轿车离甲地的距离y（千米）与时间x（小时）之间的函数关系．请根据图象解答下列问题：

(1)、货车的速度是 km/h，B点坐标为；

(2)、在轿车行驶过程中，轿车行驶多长时间两车相遇？

(3)、直接写出：在行驶过程中，货车行驶多长时间，两车相距15千米？

查看试题解析
21. 如图1，线段AB，CD交于点O，连接AC和BD，若∠A与∠B，∠C与∠D中有一组内错角成两倍关系，则称 $△ A O C$ 与 $△ B O D$ 为倍优三角形，其中成两倍关系的内错角中，较大的角称为倍优角．

(1)、如图2，在四边形ABCD中，对角线AC，BD交于点O，已知 $A B ⊥ B D$ ， $△ C O D$ 为等边三角形．求证： $△ A O B$ ， $△ C O D$ 为倍优三角形．

(2)、如图3，已知边长为2的正方形ABCD，点P为边CD上一动点（不与点C，D重合），连接AP和BP，对角线AC和BP交于点O，当 $△ A O P$ 和 $△ B O C$ 为倍优三角形时，求：∠DAP的正切值．

(3)、如图4，四边形ABCD内接于 $⊙ O$ ， $△ B C P$ 和 $△ A D P$ 是倍优三角形，且∠ADP为倍优角，延长AD，BC交于点E．若 $A B = 8$ ， $C D = 5$ ，求 $⊙ O$ 的半径．

查看试题解析
22. 如图，直线y＝﹣2x+4交x轴于点A，交y轴于点B，抛物线y＝ax²+bx+c（a≠0）经过点A、E，点E的坐标是（5，3），抛物线交x轴于另一点C（6，0）.

(1)、求抛物线的解析式.

(2)、设抛物线的顶点为D，连接BD，AD，CD，动点P在BD上以每秒2个单位长度的速度由点B向点D运动，同时动点Q在线段CA上以每秒3个单位长度的速度由点C向点A运动，当其中一个点到达终点停止运动时，另一个点也随之停止运动，设运动时间为t秒，PQ交线段AD于点H.
①当∠DPH＝∠CAD时，求t的值；

②过点H作HM⊥BD，垂足为点M，过点P作PN⊥BD交线段AB于点N.在点P、Q的运动过程中，是否存在以点P，N，H，M为顶点的四边形是矩形？若存在，求出t的值；若不存在，请说明理由.

查看试题解析

组别	成绩分组	频数	频率
A	50≤x＜60	4	0.1
B	60≤x＜70	10	0.25
C	70≤x＜80	m	n
D	80≤x＜90	8	0.2
E	90≤x≤100	6	0.15