2023学年沪科版数学七年级下册期中考试质量检测卷(一)
试卷更新日期:2023-03-30 类型:期中考试
一、单选题(每题4分,共40分)
-
1. 下列各数中,是无理数的为( )A、 B、 C、 D、2. 原子是化学变化中的最小微粒,按照国际单位制的规定,质量单位是“kg”.例如:1个氧原子的质量是 . 如果小数0.000…02657用科学记数法表示为 , 那么这个小数中的“0”有( )A、25个 B、26个 C、27个 D、28个3. 下列运算结果正确的是( )A、 B、 C、 D、4. 已知 , a介于两个连续自然数之间,则下列结论正确的是( )A、 B、 C、 D、5. 下列各式从左到右的变形中,是因式分解且完全正确的是( )A、 B、 C、 D、6. 某商畈去菜摊买黄瓜,他上午买了30千克,价格为每千克x元,下午,他又买了20千克,价格为每千克y元﹒后来他以每千克元的价格卖完后,结果发现自己赔了钱,其原因是( )A、<y B、 C、 D、7. 某种商品每件的进价为120元,商场按进价提高标价,为增加销量,准备打折销售,但要保证利润率不低于 , 则至多可以打( )折A、7 B、7.5 C、8 D、8.58. 关于的不等式组有且只有三个整数解,则的最大值是( )A、3 B、4 C、5 D、69. 如图,两个正方形边长分别为a,b,已知 , , 则阴影部分的面积为( )
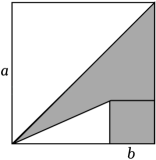 A、10 B、11 C、12 D、1310. 根据等式: , , ……的规律,则可以推算得出的末位数字是( )A、 B、 C、 D、
A、10 B、11 C、12 D、1310. 根据等式: , , ……的规律,则可以推算得出的末位数字是( )A、 B、 C、 D、二、填空题(每空4分,共20分)
-
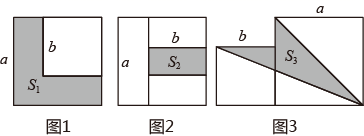
11. 比较大小:.(填“>”,“<”,或“=”)12. 已知=1.449,=4.573,则是 .13. 若是关于的完全平方式,则 .14. 两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为 ;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为 .若 ,则 + = ;当 + =40时,则图3中阴影部分的面积 .
三、解答题(共9题,共90分)
-
15. 计算:.16. 解不等式组:17. 已知:的立方根是 , c是的整数部分.(1)、求a,b,c的值;(2)、求的平方根.18. 一艘轮船从某江上游的 地匀速驶到下游的 地用了 ,从 地匀速返回 地用了不到12h,这段江水的流速为 ,轮船在静水中的往返速度不变,且为正整数.试求轮船在静水中速度的最小值是多少?19. 小明和小红在计算时,分别采用了不同的解法.
小明的解法: ,
小红的解法:.
请你借鉴小明和小红的解题思路,解决下列问题:
(1)、若 , 求的值;(2)、已知满足 , 求的值.20. [学习材料]——拆项添项法在对某些多项式进行因式分解时,需要把多项式中的某一项拆成两项或多项,或者在多项式中添上两个仅符号相反的项,这样的分解因式的方法称为拆项添项法.如:
例1:分解因式:x2+2x-3.
解:原式=x2+2x+1-1-3=(x+1)2-4=(x+1-2)(x+1+2)=(x-1)(x+3).
例2:分解因式:x3+5x-6.
解:原式=x3-x+6x-6=x(x2-1)+6(x-1)=(x-1)(x2+x+6).
[知识应用]请根据以上材料中的方法,解决下列问题:
(1)、分解因式:x2+14x-51= .(2)、化简:21. 若满足 , 求的值.解:设 , , 则 , , .
(1)、若满足 , 求的值;(2)、
【拓展应用】
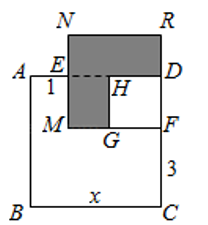
如图,已知正方形的边长为分别是上的点,且 , 长方形的面积是 , 分别以为边作正方形.① ▲ , ▲ ;(用含的式子表示)
②求阴影部分的面积.
 22. 随着新能源汽车的发展,某公交公司将用新能源汽车淘汰某一条线路上“冒黑烟”较严重的燃油公交车,计划购买A型和B型新能源公交车共10辆.若购买A型公交车1辆和B型公交车2辆共需300万元;且购买一辆A型公交车的费用比购买一辆B型公交车的费用少30万元.(1)、求A型和B型公交车的单价分别为多少万元?(2)、预计在该条线路上A型和B型公交车每辆日均载客量为160人次和200人次,若该公司购买A型和B型公交车的总费用不超过1000万元,且确保这10辆公交车在该线路的日均载客量总和不少于1800人次,则该公司有哪几种购车方案?哪种购车方案的总费用最少?最少总费用是多少?23. 若不等式组只有个正整数解为自然数 , 则称这个不等式组为阶不等式组 .
22. 随着新能源汽车的发展,某公交公司将用新能源汽车淘汰某一条线路上“冒黑烟”较严重的燃油公交车,计划购买A型和B型新能源公交车共10辆.若购买A型公交车1辆和B型公交车2辆共需300万元;且购买一辆A型公交车的费用比购买一辆B型公交车的费用少30万元.(1)、求A型和B型公交车的单价分别为多少万元?(2)、预计在该条线路上A型和B型公交车每辆日均载客量为160人次和200人次,若该公司购买A型和B型公交车的总费用不超过1000万元,且确保这10辆公交车在该线路的日均载客量总和不少于1800人次,则该公司有哪几种购车方案?哪种购车方案的总费用最少?最少总费用是多少?23. 若不等式组只有个正整数解为自然数 , 则称这个不等式组为阶不等式组 .我们规定:当时,这个不等式组为阶不等式组 .
例如:不等式只有4个正整数解,因此称其为4阶不等式.
不等式组只有3个正整数解,因此称其为3阶不等式组.
请根据定义完成下列问题:
(1)、 是阶不等式;是阶不等式组;(2)、若关于的不等式组是4阶不等式组,求的取值范围;(3)、关于的不等式组的正整数解有 , , , , 其中如果是阶不等式组,且关于的方程的解是的正整数解 , 请求出的值以及的取值范围.