2022-2023学年浙教版数学八年级下册5.1矩形课后测验

试卷更新日期：2023-03-30 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，矩形ABCD的两条对角线相交于点O，∠AOB＝60°，AO＝4，则AB的长是（）

A、4 B、5 C、6 D、8

查看试题解析
2. 如图，已知四边形 $A B C D$ 是平行四边形，下列结论中正确的是（）

A、当 $A B = B C$ 时，它是矩形 B、当 $A C ⊥ B D$ 时，它是矩形 C、当 $∠ A B C = 90 °$ 时，它是正方形 D、当 $A C ⊥ B D$ 时，它是菱形

查看试题解析
3. 如图，E为正方形ABCD的对角线上一点，四边形EFCG为矩形，若正方形ABCD的边长为4，则EG＋GC的长为（）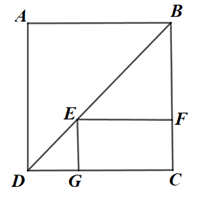

A、4 B、8 C、16 D、32

查看试题解析
4. 矩形具有而一般平行四边形不具有的性质是（）

A、两组对边分别相等 B、两组对角分别相等 C、两条对角线互相平分 D、两条对角线相等

查看试题解析
5. 如图所示的▱ABCD，再添加下列某一个条件，不能判定▱ABCD是矩形的是（）

A、AC＝BD B、AB⊥BC C、∠1＝∠2 D、∠ABC＝∠BCD

查看试题解析
6. 如图，矩形 $A B C D$ 中 $A B = 8$ 把矩形沿直线 $A C$ 折叠，点 $B$ 落在点 $E$ 处， $A E$ 交 $C D$ 于点 $F$ ．若 $A F = \frac{25}{4}$ ，则 $A D$ 的长为（）

A、4 B、5 C、6 D、7

查看试题解析
7. 矩形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点O，若 $∠ A O B = 60 °$ ， $A B = \sqrt{3}$ ，则对角线 $A C$ 的长是（）

A、3 B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、6

查看试题解析
8. 有下列说法：
①对角线相等的四边形是矩形；②对角线互相平分且相等的四边形是矩形；③有一个角是直角的四边形是矩形；④有三个角是直角的四边形是矩形；⑤四个角都相等的四边形是矩形；

⑥对角线相等，且有一个角是直角的四边形是矩形.其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
9. 如图，在Rt△ABC中，∠BAC＝90°，AB＝AC＝16cm，AD为BC边上的高．动点P从点A出发，沿A→D方向以cm/s的速度向点D运动．设△ABP的面积为S₁ ，长方形PDFE的面积为S₂ ，运动时间为t秒（0＜t＜8），则t＝（）秒时，S₁＝2S₂ ．

A、5 B、6 C、7 D、8

查看试题解析
10. 如图，线段 $A B$ 的长为 $8$ ，点 $D$ 在 $A B$ 上， $Δ A C D$ 是边长为 $3$ 的等边三角形，过点 $D$ 作与 $C D$ 垂直的射线 $D P$ ，过 $D P$ 上一动点 $G$ （不与 $D$ 重合）作矩形 $C D G H$ ，记矩形 $C D G H$ 的对角线交点为 $O$ ，连接 $O B$ ，则线段 $B O$ 的最小值为（）

A、5 B、4 C、 $4 \sqrt{3}$ D、 $5 \sqrt{3}$

查看试题解析

二、填空题

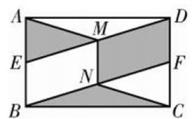
11. 在矩形ABCD中，对角线AC、BD相交于点O，∠AOB＝60°，AC＝6cm，则AB的长是．

查看试题解析
12. 若矩形的面积为a²+ab，宽为a，则长为．

查看试题解析
13. 木工师傅要做一张长方形的桌面．完成后，量得桌面的长为 $100 c m$ ，宽为 $80 c m$ ，对角线为130cm，则做出的这个桌面.（填“合格”或“不合格”）

查看试题解析
14. 如图，矩形ABCD中，点E，F分别是AB，CD的中点，连接DE和BF，分别取DE，BF的中点M，N，连接AM， CN，MN，若AB=2，BC=3，则图中阴影部分的面积为.

查看试题解析
15. 如图1，矩形纸片ABCD， AB=5， BC=8．将此矩形纸片按下列顺序折叠，则图4中MN的长为．

查看试题解析
16. 如图所示，顺次连结四边形ABCD各边中点得四边形GHEF，要使四边形GHEF为矩形，则四边形ABCD 的对角线AC，BD 应满足的条件是.

查看试题解析

三、解答题

17. 如图，四边形 $A B C D$ 是矩形，点 $E$ 在 $A D$ 上， $E F ⊥ E C$ 交 $A B$ 于点 $F$ ，且 $E F = E C$ ， $D E = 2$ ，矩形的周长为16；求 $A E$ 的长．

查看试题解析
18. 如图，在△ABC中，AB＝AC，AD⊥BC于点D，过点B作AD的平行线交外角∠BAF的平分线于点E．求证：四边形ADBE是矩形．

查看试题解析
19. 如图，在△ABC中，AB=AC，D为BC中点，四边形ABDE是平行四边形，求证：四边形ADCE是矩形.

查看试题解析
20. 如图所示，在矩形ABCD中， $A B = 3$ ， $A D = 4$ ，过点A，C的两条直线相交于点E．若 $A E = 13$ ， $C E = 12$ ，求图中阴影部分的面积．

查看试题解析
21. 已知：如图，在矩形ABCD中，E、F分别是边CD、AD上的点， $A E ⊥ B F$ ，且 $A E = B F$ ．求证：矩形ABCD是正方形．

查看试题解析
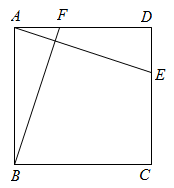22. 阅读下列材料并完成相应的任务
等面积法是一种常用的、重要的数学解题方法．它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题．在解题中，灵活运用等面积法解决相关问题，可以使解题思路清晰，解题过程简便快捷．
如图，矩形 $A B C D$ 的边 $A B$ 上有一动点E，以 $E C$ 为边作 $▱ E C F G$ ，且边 $F G$ 过矩形的顶点D，在点E从点A移动到点B的过程中， $▱ E C F G$ 的面积如何变化？
小亮的观点：过点D作 $D H ⊥ C E$ 于点H，连接 $D E$ ． $C E$ 与 $D H$ 的乘积始终等于 $C D \cdot A D$ ，所以 $▱ E C F G$ 的面积不变．
小明的观点：在点E的运动过程中， $C E$ 的长度在变化，而 $C E$ 与 $F G$ 两条平行线间的距离不变，所以 $▱ E C F G$ 的面积变化．
任务：你认为小亮和小明谁的观点正确？正确的写出完整的证明过程．

查看试题解析
23. 矩形ABCD中，AB=3，BC=4.点E，F在对角线AC上，点M，N分别在边AD，BC上.

(1)、如图1，若AE=CF=1，M，N分别是AD，BC的中点.求证：四边形EMFN为矩形.

(2)、如图2，若AE=CF=0.5， $A M = C N = x （ 0 < x < 2 ）$ ，且四边形EMFN为矩形，求x的值.

查看试题解析
24. 【操作】如图①，在矩形 $A B C D$ 中，E为对角线 $A C$ 上的一点（不与点A重合）．将 $△ A D E$ 沿射线 $A B$ 方向平移到 $△ B C F$ 的位置，点E的对应点为点F，易证： $△ A D E ≌ △ B C F$ （不需要证明）；
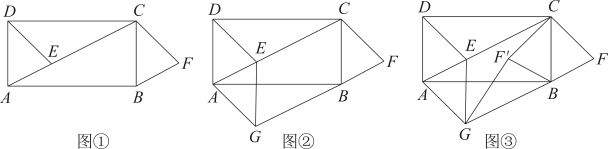
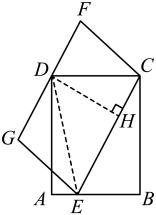
【探究】过图①的点E作 $E G ∥ B C$ ，交 $F B$ 的延长线于点G，连接 $A G$ ，其他条件不变，如图②．求证： $△ E G A ≌ △ B C F$ ；
【拓展】将图②中的 $△ B C F$ 沿 $B C$ 翻折得到 $△ B C F^{'}$ ，连接 $G F^{'}$ ，其他条件不变，如图③．当 $G F^{'}$ 最短时，若 $A B = 4$ ， $B C = 2$ ，直接写出四边形 $B F C F^{'}$ 的周长．

查看试题解析

2022-2023学年浙教版数学八年级下册5.1矩形 课后测验

一、单选题

二、填空题

三、解答题

2022-2023学年浙教版数学八年级下册5.1矩形课后测验