2022-2023学年浙教版数学八年级下册4.6反证法 课后测验
试卷更新日期：2023-03-30 类型：同步测试
一、单选题
-
1. 用反证法证明命题“四边形中至少有一个角是钝角或直角”时，首先应该假设这个四边形中（ ）A、有一个角是钝角或直角 B、每一个角都是锐角 C、每一个角都是直角 D、每一个角都是钝角2. 用反证法证明“a＞b”时，应假设（ ）A、a＜b B、a≤b C、a＝b D、a≥b3. 用反证法证明命题“在三角形中，至少有一个内角大于或等于60°”时，先假设（ ）A、每个内角都小于60° B、每个内角都大于60° C、没有一个内角小于等于60° D、每个内角都等于60°4. 用反证法证明命题“在直角三角形中，必有一个锐角不小于45°”时，首先应假设这个直角三角形中（ ）A、两个锐角都大于45° B、两个锐角都小于45° C、两个锐角都不大于45° D、两个锐角都等于45°5. 用反证法证明：“一个三角形中至多有一个角不小于90°”时，应假设（ ）A、一个三角形中至少有两个角不小于 90° B、一个三角形中至多有一个角不小于 90° C、一个三角形中至少有一个角不小于 90° D、一个三角形中没有一个角不小于 90°6. 要说明命题“两个无理数的和是无理数”，可选择的反例是（ ）A、2，﹣3 B、 ， C、 ，﹣ D、 ，7. 如图，在△ABC中，AB＝AC，∠APB≠∠APC，求证：PB≠PC，当用反证法证明时，第一步应假设（ ）
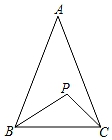A、AB≠AC B、PB＝PC C、∠APB＝∠APC D、∠B≠∠C8. 已知 中， ，求证： ，下面写出运用反证法证明这个命题的四个步骤：①∴ ，这与三角形内角和为 矛盾②因此假设不成立．∴ ③假设在 中， ④由 ，得 ，即 ．
这四个步骤正确的顺序应是（ ）
A、④③①② B、③④②① C、①②③④ D、③④①②9. 下列命题正确的是（ ）A、三角形三条角平分线的交点到三角形三个顶点的距离都相等 B、两条对角线相等的四边形是平行四边形 C、分式 的值不能为零 D、用反证法证明“三角形中必有一个角不大于60”，先假设这个三角形中有一个内角大于60°10. 公元前500年，毕达哥拉斯学派中的一名成员西伯索斯发现了无理数，导致了第一次数学危机．事实上，我国古代发现并阐述无理数的概念比西方更早，但是没有系统的理论．《九章算术》的开方术中指出了存在有开不尽的情形：“若开方不尽者，为不可开．”《九章算术》的作者们给这种“不尽根数”起了一个专门名词—“面”“面”就是无理数．无理数中最具有代表性的数就是“”．下列关于的说法错误的是（ ）A、可以在数轴上找到唯一一点与之对应 B、它是面积为2的正方形的边长 C、可以用两个整数的比表示 D、可以用反证法证明它不是有理数二、填空题
-
11. 用反证法证明，“在△ABC中，∠A、∠B对边是a、b，若∠A>∠B，则a>b．"第一步应假设12. 反证法证明“钝角三角形中必有一个角小于45°”先应假设.13. 用反证法证明“树在道边而多子，此必苦李”时，应首先假设：。14. 用反证法证明“若|a|>2，则a2>4”时，应假设。15. 某校九年级四个班的代表队准备举行篮球友谊赛．甲、乙、丙三位同学预测比赛的结果如下：甲说：“902班得冠军，904班得第三”；乙说：“901班得第四，903班得亚军”；丙说：“903班得第三，904班得冠军”．赛后得知，三人都只猜对了一半，则得冠军的是 ．16.
用反证法证明命题“已知：如图，L1与L2不平行，求证：∠1≠∠2”．证明时应假设 ．
三、解答题
-
17. 用反证法证明：等腰三角形的底角必定是锐角.18. 阅读下列文字，回答问题。
题目：如图，在Rt△ABC中，∠C=90°，若∠A≠45°，则AC≠BC.
证明：假设AC=BC，
∠A≠45°，∠C=90°，∴∠A≠∠B
∴AC≠BC，这与假设矛盾，∴AC≠BC.
上面的证明有没有错误？若没有错误，指出其证明的方法；若有错误，请予以纠正。
19. 用反证法求证：三角形的一个外角等于与它不相邻的两个内角的和.已知：如图，∠1是△ABC的一个外角.
求证：∠1＝∠A+∠B.
