2022-2023学年浙教版数学八年级下册4.5三角形的中位线 课后测验
试卷更新日期:2023-03-30 类型:同步测试
一、单选题
-
1. 如图,在△ABC中,D、E分别是AB、AC边上的中点,若DE=4,则BC等于( )
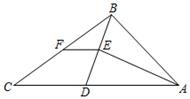
 A、2 B、4 C、8 D、122. 如图,为了测量池塘边、两地之间的距离,在线段的同侧取一点 , 连结并延长至点 , 连结并延长至点 , 使得、分别是、的中点,若 , 则线段的长度是( )
A、2 B、4 C、8 D、122. 如图,为了测量池塘边、两地之间的距离,在线段的同侧取一点 , 连结并延长至点 , 连结并延长至点 , 使得、分别是、的中点,若 , 则线段的长度是( ) A、 B、 C、 D、3. 如图,在中,分别取AB、AC的中点D、E,连接DE,过点A作 , 垂足为F,将分割后拼接成矩形BCHG,若 , , 则的面积是( )
A、 B、 C、 D、3. 如图,在中,分别取AB、AC的中点D、E,连接DE,过点A作 , 垂足为F,将分割后拼接成矩形BCHG,若 , , 则的面积是( )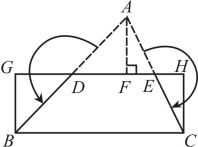 A、8 B、10 C、14 D、164. 如图,在Rt△ABC中,∠ACB=90°,CM是斜边AB上的中线,E、F分别为MB、BC的中点,若EF=1,则AB等于( )
A、8 B、10 C、14 D、164. 如图,在Rt△ABC中,∠ACB=90°,CM是斜边AB上的中线,E、F分别为MB、BC的中点,若EF=1,则AB等于( ) A、3 B、 C、4 D、5. 如图,在中, , , 是边上的中线.按下列步骤作图:①分别以点和点为圆心,大于的长为半径作弧,两弧相交于点 , ;②作直线 , 分别交 , 于点 , ;③连接 , . 则下列结论错误的是( )
A、3 B、 C、4 D、5. 如图,在中, , , 是边上的中线.按下列步骤作图:①分别以点和点为圆心,大于的长为半径作弧,两弧相交于点 , ;②作直线 , 分别交 , 于点 , ;③连接 , . 则下列结论错误的是( ) A、 B、 C、 D、6. 如图,是内一点, , , , , , , , 分别是 , , , 的中点,则四边形的周长为( )
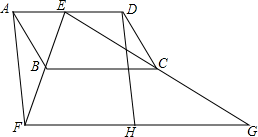
A、 B、 C、 D、6. 如图,是内一点, , , , , , , , 分别是 , , , 的中点,则四边形的周长为( ) A、20 B、24 C、36 D、417. 如图,在平行四边形ABCD中,对角线AC⊥BC,M在∠CAD的平分线上,且AM⊥DM,点N为CD的中点,连接MN,若AD=12,MN=2.则AB的长为( )
A、20 B、24 C、36 D、417. 如图,在平行四边形ABCD中,对角线AC⊥BC,M在∠CAD的平分线上,且AM⊥DM,点N为CD的中点,连接MN,若AD=12,MN=2.则AB的长为( )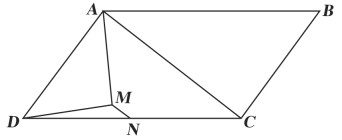 A、12 B、20 C、24 D、308. 如图,▱的对角线 , 交于点 , 是的中点,连结 , , , 若 , 则等于( )
A、12 B、20 C、24 D、308. 如图,▱的对角线 , 交于点 , 是的中点,连结 , , , 若 , 则等于( ) A、3 B、4 C、5 D、69. 如图,四边形ABCD中,AB∥CD,AB=5,DC=11,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是( )
A、3 B、4 C、5 D、69. 如图,四边形ABCD中,AB∥CD,AB=5,DC=11,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是( ) A、8 B、9 C、10 D、1210. 如图所示,点E为平行四边形ABCD对角线AC上的一点,AE=7,CE=3,点F在BE的延长线上.且EF=BE,EF与CD相交于点G,则DF=( )
A、8 B、9 C、10 D、1210. 如图所示,点E为平行四边形ABCD对角线AC上的一点,AE=7,CE=3,点F在BE的延长线上.且EF=BE,EF与CD相交于点G,则DF=( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
11. 如图,已知在中,、分别是、的中点,、分别是、的中点,且 , 则的长度是 .
 12. 如图,如果要测量池塘两端A,B的距离,可以在池塘外取一点C,连接AC,BC,点D,E分别是AC,BC的中点,测得DE的长为25米,则AB的长为 米.
12. 如图,如果要测量池塘两端A,B的距离,可以在池塘外取一点C,连接AC,BC,点D,E分别是AC,BC的中点,测得DE的长为25米,则AB的长为 米.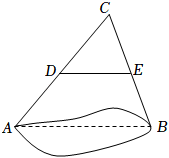 13. 如图,每个小正方形的边长为1,在△ABC中,点D、E分别为AB、AC的中点,则线段DE的长为.
13. 如图,每个小正方形的边长为1,在△ABC中,点D、E分别为AB、AC的中点,则线段DE的长为. 14. 如图,点D、E、F分别是△ABC三边的中点,若△ABC的周长为12,则△DEF的周长为 .
14. 如图,点D、E、F分别是△ABC三边的中点,若△ABC的周长为12,则△DEF的周长为 . 15. M、N分别是△ABC中AB、AC的中点,若BC=6,则MN= .16. 如图,平行四边形ABCD中,点O是对角线AC的中点,点E在边AB上,连接DE , 取DE的中点F , 连接EO并延长交CD于点G . 若BE=3CG , OF=2,则线段AE的长是 .
15. M、N分别是△ABC中AB、AC的中点,若BC=6,则MN= .16. 如图,平行四边形ABCD中,点O是对角线AC的中点,点E在边AB上,连接DE , 取DE的中点F , 连接EO并延长交CD于点G . 若BE=3CG , OF=2,则线段AE的长是 .
三、解答题
-
17. 如图,在△ABC和△ABD中,∠ACB=∠ADB=90°,E、F、G分别为AB、AC、BC的中点,若DE=1,则FG= .
 18. 如图,点D、F分别为AC、BC的中点, , ,求证:
18. 如图,点D、F分别为AC、BC的中点, , ,求证: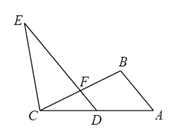 19. 如图,在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点,顺次连接E,F,G,H,得到的四边形EFGH叫中点四边形.求证:四边形EFGH是平行四边形.
19. 如图,在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点,顺次连接E,F,G,H,得到的四边形EFGH叫中点四边形.求证:四边形EFGH是平行四边形.