2022-2023学年浙教版数学八年级下册4.4平行四边形的判定 课后测验
试卷更新日期：2023-03-30 类型：同步测试
一、单选题
-
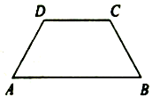
1. 如图，在一束平行光线中插入一张对边平行的纸板，如果光线与纸板右下方所成的 ， 则光线与纸板左上方所成的的度数是（ ）
A、 B、 C、 D、2. 如图，平行四边形中， ， 是对角线上的两点，如果添加一个条件使四边形是平行四边形，则添加的条件不能是（ ）
A、 B、 C、 D、3. 在平面直角坐标系中，以A（-1，0），B（2，0），C（0，1），为顶点构造平行四边形，下列各点中不能作为平行四边形第四个顶点的坐标的是（ ）
A、 B、 C、 D、4. 如图，在△ABC中，D，E分别是AB，BC的中点，点F在DE延长线上，添加一个条件使四边形ADFC为平行四边形，则这个条件是（ ）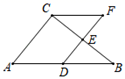
A、∠B＝∠F B、∠B＝∠BCF C、AC＝CF D、AD＝CF5. 在复习平行四边形的判定方法时，某同学进行了画图探究，其作法和图形如下：①如图1，作线段AC的垂直平分线，交AC于点O；②如图2，过点O作一条直线l（不过点A，C）再以点O为圆心，任意长为半径作弧，交直线l于点B，D，连接AB，BC，CD，AD．根据以上作法，不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是（ ）
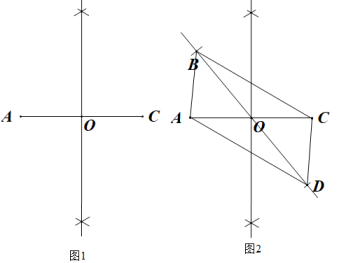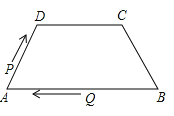
A、对角线互相平分的四边形是平行四边形 B、两组对边分别平行的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、两组对边分别相等的四边形是平行四边形6.如图，在四边形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动，同时点Q从点B出发，以1个单位/s的速度沿BA向终点A运动．当四边形PQBC为平行四边形时，运动时间为（ ）
A、4s B、3s C、2s D、1s7. 如图，分别以的斜边、直角边为边向外作等边和等边 ， 为的中点，连接、 ， 与相交于点 ， 若 ， 下列结论：①；②四边形为平行四边形；③；④ ． 其中正确结论有（ ）
A、1个 B、2个 C、3个 D、4个8. 如图四边形ABCD的对角线AC，BD交于点O，则不能判断四边形ABCD是平行四边形的是（ ）
A、AB∥CD，∠DAC=∠BCA B、AB=CD，∠ABO=∠CDO C、AC=2AO，BD=2BO D、AO=BO，CO=DO9. 下列不能判断一个四边形是平行四边形的是（ ）A、一组对边平行且相等的四边形 B、两组对边分别相等的四边形 C、对角线互相平分的四边形 D、一组对边相等，且另一组对边平行的四边形10. 已知四边形 ，有以下四个条件： ； ； ； 从这四个条件中选两个，下列不能确定四边形 为平行四边形的是（ ）A、 B、 C、 D、二、填空题
-
11. 已知：如图，四边形 中， ，要使四边形 为平行四边形，需添加一个条件是：.(只需填一个你认为正确的条件即可)
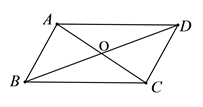12. 如图，已知△ABC中，D，E分别是AB，AC的中点，连接DE并延长至F．使EF＝DE，连接CF．若∠B＝45°，则的度数为 ．
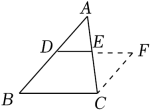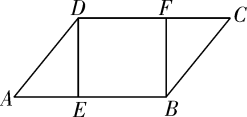
13. 四边形ABCD中，AB∥CD，AB=4，当CD=时，四边形ABCD是平行四边形．14. 已知：如图，线段AB＝6cm，点P是线段AB上的动点，分别以AP、BP为边在AB作等边APC、等边BPD，连接CD，点M是CD的中点，当点P从点A运动到点B时，点M经过的路径的长是cm．
15. 如图四边形ABCD ， AD∥BC ， AB⊥BC ， AD＝1，AB＝2，BC＝3，P为AB边上的一动点，以PD ， PC为边作平行四边形PCQD ， 则对角线PQ的长的最小值是.
16. 已知直线l及线段AB，点B在直线上，点A在直线外．如图，
⑴在直线l上取一点C（不与点B重合），连接AC；
⑵以点A为圆心，BC长为半径作弧，以点B为圆心，AC长为半径作弧，两弧交于点D（与点C位于直线AB异侧）；
⑶连接CD交AB于点O，连接AD，BD．
根据以上作图过程及所作图形，在下列结论①OA＝OB；②；③∠ACD＝∠ADC中，一定正确的是（填写序号）．
三、解答题
-
17. 如图，已知点E、F分别在▱ABCD的边AB、CD上，且AE=CF.求证：DE=BF.
18. 如图，E、F分别是▱ABCD的边AD、BC上的点，且AE=CF，AF和BE相交于点G，DF和CE相交于点H，求证：EF和GH互相平分．
19. 如图，已知∠A=∠D，AB=DE，AF=CD，BC=EF．求证：BC∥EF．
20. 如图，在Rt△ABC中，∠ACB=90°，D、E分别是AB、AC的中点，连接CD，过E作EF∥DC交BC的延长线于F．
(1)、证明：四边形CDEF是平行四边形；(2)、若四边形CDEF的周长是25cm，AC的长为5cm，求线段AB的长度．
